Aplikacja solwera iteracyjnego jest zalecana do rozwiązywania liniowych zadań statycznych wielowymiarowych (równania 15 000 - 1 000 000) oraz problemów wartości własnej (analiza wyboczeniowa lub modalna). Tradycyjne metody bezpośrednie (frontalalna, skyline, rzadka) są bardzo czasochłonne i wymagają dużej ilości miejsca na dysku do przechowywania macierzy po faktoryzacji. Takie podejście może okazać się bardzo wydajne dla analizy konstrukcji zawierających bryłę ES. Solwery tego typu mogą być bardzo przydatne podczas liniowej analizy statycznej ( na przykład podczas wyszukiwania optymalnych parametrów wymiarowania), gdy jest możliwe uzyskanie rozwiązania przybliżonego dla małej liczby przypadków obciążeń. Kontrola poprawności danych "element po elemencie" zgodnie z regularyzacją Wingeta (jak pokazano poniżej) stanowi dodatkową aplikację solwera iteracyjnego, która umożliwia wykrywanie problemów podczas znajdowania błędów w modelu ES.
W metodzie gradientowej z uwarunkowaniem wstępnym (PCG) jest obecnie możliwe zwieranie kilku typów uwarunkowań wstępnych.
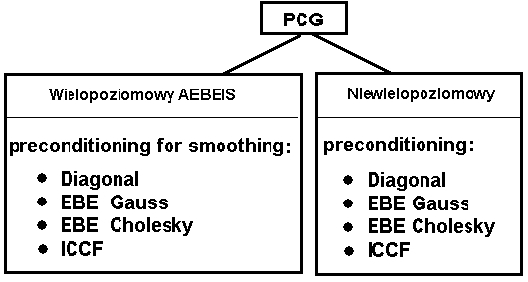
- AEBEIS: Agregacyjna, iteracyjna procedura rozwiązania równań "element-po-elemencie" 1,2
- EPE: Element po elemencie
- ICCF: Podejście niekompletnego rozkładu Choleskiego
AEBEIS jest wielopoziomową, agregacyjną, iteracyjną procedurą rozwiązania "element po elemencie", która łączy zalety szybkich metod iteracyjnych z niedrogą techniką EPE. Umożliwia ona przyspieszenie podstawowych operacji za pomocą metod niedrogich pod względem wymagań pamięci. Metody agregacyjne, takie jak ta, umożliwiają analizę brył i powłok (podobnie jak to robi metoda wielosiatkowa), jak również prętów i konstrukcji kombinowanych z prętów, powłok i brył.
AEBEIS zazwyczaj zapewnia szybszą konwergencję w porównaniu do metod niewielopoziomowych. Jest ona ograniczona tylko do konstrukcji 3D i ram 2D. AEBEIS wskazuje mniejszą wrażliwość na problemy złego uwarunkowania niż odpowiednie metody iteracyjne, niewielopoziomowe, ale jest mniej bezpieczna. W rzadkich przypadkach występuje "blokada" warunków wstępnych, ale konwergencja nadal jest powolna.
AEBEIS umożliwia zastosowanie elementów prętowych 2D i 3D, elementów powłokowych (elementów węzłowych: 3, 4, 6, 8) i elementów bryłowych. Umożliwia ona również dodatkowe elelementy składnikowe konstrukcji, takie jak podpory sprężyste, offsety, zwolnienia i połączenia sztywne. Dla metody niewielopoziomowej nie ma ograniczeń dotyczących typów elementu lub konstrukcji.
Następujące typy uwarunkowania wstępnego są dostępne zarówno w AEBEIS, jak i w metodzie niewielopoziomowej.
- Diagonalna - uwarunkowanie wstępne Jacobiego (stosować tylko w przypadku dobrze uwarunkowanych problemów).
- EPE Gaussa - zmodyfikowane uwarunkowanie wstępne EPE Gaussa-Seidela-Choleskiego 1,2 .
- EPE Choleskiego - uwarunkowanie wstępne EPE Choleskiego 1,4 .
- ICCF - podejście niekompletnego rozkładu Choleskiego 5,6 .
Podejście ICCF jest szybsze od innych metod (diagonalnej, EPE Gaussa, EPE Choleskiego) i używa w przybliżeniu tej samej liczby iteracji, aby uzyskać konwergencję, taką jak metody EPE Gaussa lub EPE Choleskiego. Nie wykorzystuje ono operacji I/O z dysku, ale zachowuje wyższ wymagania RAM. ICCF jest preferowana, jeśli komputer ma wystarczającą ilość pamięci RAM dla zadania. Pamięć RAM i wymagania dysku, jakich potrzebują metody EPE Gaussa i EPE Choleskiego są minimalne, ale są one wolniejsze niż podejście ICCF.
Odnośniki
- Fialko S.Yu. High-performance aggregation element-by-element iterative solver for large-scale complex shell structure problems. Archives of Civil Engineering, XLV, 2, 1999. P.193-207.
- Fialko S., High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis, CAMES, 7: 537-550, 2000.
- Hughes T.J.R., Ferencz M. Implicit solution of large-scale contact and impact problems employing an EBE preconditioned iterative solver, IMPACT 87 Int. Conference on Effects of Fast Transient Loading in the Context of Structural Mechanics, Lausanne, Switzerland, August 26-27, 1987.
- Hughes T.J.R., R.M.Ferencz, i j.O.Hallquist. Large-scale vectorized implicit calculations in solid mechanics on a CRAY X-MP/48 utilizing EBE preconditioned conjugate gradients, Comput. Meths. Appl. Mech. Engrg., 61.
- S.Bitzarakis, M.Papadrakakis, A.Kotsopulos. Parallel solution techniques in computational structural mechanics. Comp. Methods Appl. Mech. Engrg. 1997, 148, str.75-104.
- M.Papadrakakis, Solving large - scale problems in mechanics, John Wiley & Sons Ltd., 1993.
Patrz również:
Parametry solwera iteracyjnego
Solwery dostępne w programie Robot
Zalecenie praktyczne dotyczące wyboru parametrów solwerów iteracyjnych