Mooney-Rivlin-Materialeigenschaften

Das Mooney-Rivlin-Materialmodell ist ein hyperelastisches Materialmodell, das für 2D-, Ziegel-, Tetraeder-, Membran- und Schalenelemente verfügbar ist. Die Mooney-Rivlin-Materialeigenschaften sind weiter unten aufgeführt. Zusätzlich zu diesen Eigenschaften kann es erforderlich sein, Isotrope Materialeigenschaften zu definieren.

Klicken Sie auf die Schaltfläche Kurvenanpassung im Dialogfeld Elementenmaterial angeben, um die Kurve einpassen-Routine zu verwenden. Diese Routine berechnet die Materialkonstanten anhand von Spannungs-/Dehnungsdaten.

Die potenzielle Funktion des Materials lautet für verschiedene Ordnungen wie folgt:

Standard mit 2 Konstanten:

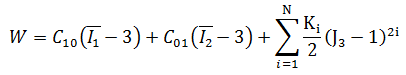
Höhere Ordnung mit 5 Konstanten:

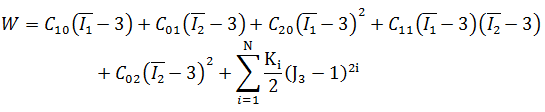
Höhere Ordnung mit 9 Konstanten:

Unabhängig von der Reihenfolge hängen das erste Schermodul, μ₀ und das Massenmodul, k₀, nur vom Polynom-Koeffizienten der Ordnung N=1 ab:

μ₀ = 2(C₁₀ + C₀₁) , k₀ = K₁

Die Mooney-Rivlin-Formel kann als eine Erweiterung der neo-hookeschen Formel betrachtet werden, in der ein Term hinzugefügt wird, der von zweiten Invarianten des linken Cauchy-Freen-Tensor abhängt. In einigen Fällen führt diese Formel zu einer genaueren Anpassung an die experimentellen Daten als die neo-hookesche Formel. Im Allgemeinen wird mit beiden Modellen eine ähnliche Genauigkeit erzielt, da sie nur lineare Funktionen der Invarianten verwenden. Diese Funktionen lassen keine Darstellung der "Auslenkung nach oben" bei höheren Dehnungsgraden in der Spannungs-Dehnungs-Kurve zu.

Massenelastizitätsmodul:

Das Massenelastizitätsmodul wird über die folgende Gleichung ermittelt: E/3*(1-2v), wobei E das Elastizitätsmodul des Materials und v der Poisson-Koeffizient des Materials ist.

Erste und zweite Konstanten:

Der Mooney-Rivlin-Ausdruck σ = 2(C₁ + C₂/λ)(λ - 1/λ²) kann verändert werden und zu folgender Formel werden: σ / [2(λ - 1/λ²)] = C₂ + λ^-1 + C₁. Dies entspricht einem linearen Ausdruck der Form y=mx+b, wobei gilt:

• m ist die Flanke, die der zweiten Mooney-Rivlin-Konstanten C₂ entspricht.
• b ist der y-Schnittpunkt, der der ersten Mooney-Rivlin-Konstante C₁ entspricht.

(In Materialmodellen höherer Ordnung und den obigen Gleichungen werden die erste und die zweite Konstante mit C₁₀ bzw. C₀₁ angegeben.)

Anmerkung: Die Mooney-Rivlin-Formel wurde von unterschiedlichen Quellen in unterschiedlichen Formen geschrieben. Stellen Sie bei der Verwendung von Mooney-Rivlin-Konstanten in der Software sicher, dass die für C₁ und C₂ eingegebenen Werte im gleichen Verhältnis zu σ stehen, wie in der Gleichung weiter oben angegeben ist. Achten Sie außerdem auf eine konsistente Verwendung der Einheiten bei der Dateneingabe und Modellierung.