Von Mises-Materialeigenschaften

Von Mises-Materialmodelle sind für 2D-, Balken-, Gehäuse-, Quader- und Tetraederelemente verfügbar. Diese Materialmodelle werden verwendet, wenn ein elastisches Material über die Streckgrenze des Materials hinaus belastet werden soll. In diesem Fall kommt es zu einer plastischen Verformung. Das Materialmodell 'von Mises-Spannung mit Härtung' verwendet eine bilineare Kurve zum Berechnen der Belastungswerte. Der elastische Bereich der Belastung weist im Vergleich zur Dehnung ein Gefälle auf, das dem Elastizitätsmodul entspricht. Der starre Belastungsbereich weist im Verhältnis zur Dehnung ein Gefälle auf, das dem Härtemodul der Dehnung entspricht.

Es stehen zwei Arten von Härtungs-Materialmodellen zur Verfügung. Das isotrope Härtungsmodell umfasst das gleichmäßige Ziehen der gesamten Zugfläche. Die kinematische Härtung umfasst eine Verlagerung der Zugfläche (vor allem aufgrund einer Belastungsumkehr). Siehe Abbildungen 1 und 2 Das kinematische Härtungsmodell wird für Analysen bevorzugt, bei denen es um zyklische Belastung geht (Bauschinger-Effekt). Das Belastungs-/Dehnungsverhalten des Materials muss jedoch als Grundlage für die Entscheidung zu Gunsten von isotropischer oder kinematischer Härtung verwendet werden.

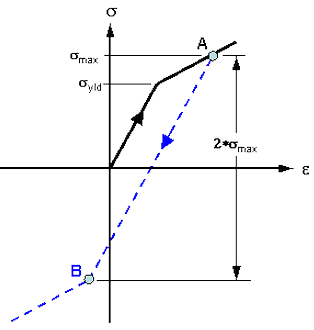
Uniaxiale Belastungs-/Dehnungskurve. Wird das Bauteil über die Zugstärke hinaus belastet, beginnt die plastische Verformung. Wird die Last bei einer maximalen Belastung (Punkt A) eliminiert, erfolgt die Entlastung entlang der gestrichelten Linie. Wird das Bauteil erneut belastet, erfolgt keine weitere plastische Verformung, bis die Belastung den Punkt A erreicht.

Bei einer Komprimierung des Bauteils wird dieses elastisch entlang von der gestrichelten Linie komprimiert, bis Punkt B erreicht ist. Anschließend gibt es der Komprimierung nach.

Bei isotropischer Härtung entspricht die Belastungsänderung von Punkt A zu Punkt B der doppelten maximal erzielten Belastung.

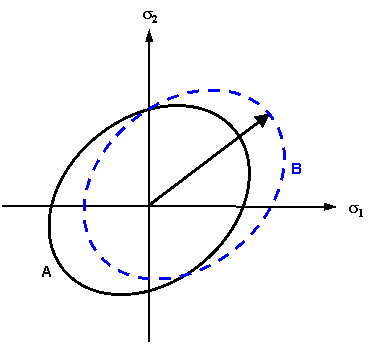
Biaxiale Belastungs-/Dehnungskurve Im biaxialen Fall finden sich im elastischen Bereich beliebige Belastungskombinationen in der Ausgangsfläche (Fläche A). Wird das Bauteil über die Ausgangsfläche hinausgeführt, kommt es zu einer plastischen Verformung.

Bei isotropischer Härtung bleibt der Mittelpunkt der Fließfläche identisch, während sich die Größe der Fläche verändert. Alle Belastungszustände in der neuen Fließfläche (Fläche B) erfahren eine plastische Verformung. Eine weitere plastische Verformung tritt ein, wenn der Belastungszustand die Fläche B erreicht.

  Abbildung 1: Isotropische Härtung 

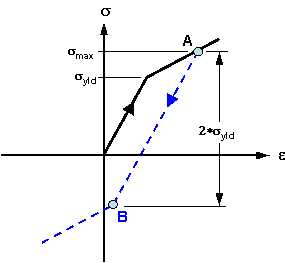
Uniaxiale Belastungs-/Dehnungskurve Wird das Bauteil über die Zugstärke hinaus belastet, beginnt die plastische Verformung. Wird die Last bei einer maximalen Belastung (Punkt A) eliminiert, erfolgt die Entlastung entlang der gestrichelten Linie. Wird das Bauteil erneut belastet, erfolgt keine weitere plastische Verformung, bis die Belastung den Punkt A erreicht.

Bei einer Komprimierung des Bauteils wird dieses elastisch entlang von der gestrichelten Linie komprimiert, bis Punkt B erreicht ist. Anschließend gibt es der Komprimierung nach.

Bei kinematischer Härtung entspricht die Belastungsänderung von Punkt A zu Punkt B der doppelten Zugbelastung.

Biaxiale Belastungs-/Dehnungskurve Im biaxialen Fall finden sich im elastischen Bereich beliebige Belastungskombinationen in der Ausgangsfläche (Fläche A). Wird das Bauteil über die Ausgangsfläche hinausgeführt, kommt es zu einer plastischen Verformung.

Bei kinematischer Härtung verlagert sich der Mittelpunkt der Fließfläche, aber die Größe der Fläche bleibt konstant. Alle Belastungszustände in der neuen Fließfläche (Fläche B) erfahren eine elastische Verformung. Eine zusätzliche plastische Verformung tritt ein, wenn der Belastungszustand die Fläche B erreicht.

Abbildung 2: Kinematische Härtung

Die von Mises-Materialeigenschaften werden nachfolgend aufgeführt. Die von Mises-Materialeigenschaften sind für beide Modelle identisch. Es kann außerdem erforderlich werden, einige isotropische Materialeigenschaften zu definieren.

Streckgrenze

Die Streckgrenze des Materials ist der Punkt auf der Spannung-/Dehnungskurve, an dem das Material in eine plastische Verformung übergeht. Nach einmaligem Strecken variiert die neue Zugstärke je nach Härtung und Belastungshistorie.

Dehnungsverfestigungsmodul

Das Dehnungsverfestigungsmodul ist das Gefälle von Belastung im Vergleich zur Dehnungskurve, nach dem Streckpunkt eines Materials.

Werden die Materialeigenschaften eines Bauteils aus einer Materialbibliothek geladen, basiert das Dehnungsverfestigungsmodul auf den drei Punkten, die die bilineare Belastungs-/Dehnungskurve definieren: (0,0), der Zugpunkt und ein dritter Punkt, der in der Bibliotheksverwaltung als Endstärke und Ausdehnung bei 2 in definiert wird. Das Dehnungsverfestigungsmodul wird wie folgt berechnet:

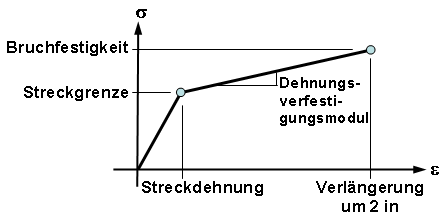
Dehnungsverfestigungsmodul = [Endstärke - Zugstärke]/[(Ausdehnung bei 2 in)/100 - Zugbelastung]

 

Hierbei ist die Zugbelastung die der Zugstärke entsprechende Belastung, oder Zugbelastung = (Zugstärke) / (Elastizitätsmodul). Die Endstärke, Zugstärke, Ausdehnung bei 2 in und das Elastizitätsmodul werden in der Materialbibliothek gespeichert.

Strukturelle Instabilität

Bei Verwendung eines von Mises-Materialmodells nimmt die Steifheit der Struktur ab, und die Struktur kann instabil werden, wenn die Streckgrenze des Materials überschritten wird. In diesem Zustand ist die Fähigkeit der Struktur zum Tragen der angewendeten Last im Vergleich zu einem Zustand, in dem alle Spannungen im elastischen Bereich liegen, erheblich verringert. Diese Instabilität zeigt sich u. a. in Form von Schwierigkeiten bei der numerischen Lösungskonvergenz und instabilen oder unregelmäßigen Spannungsergebnissen. In dieser Situation erweisen sich die folgenden Anpassungen bei der Modelleinrichtung als nützlich:

Übergeordnetes Thema: Materialeigenschaften