- Eine Zwangsverschiebung führt zu einer Verschiebung oder Drehung des Knotens über eine bestimmte Distanz hinweg, die im Feld Betrag angegeben ist. Diese Verschiebung oder Drehung kann entlang eines Vektors erfolgen, der im Bereich Richtung angegeben ist.
- Die Verschiebung des Knotens zu einem beliebigen Zeitpunkt in der Analyse bezieht sich auf den Betrag, der der Zwangsverschiebung zugewiesen ist, und auf den in der Lastkurve angegebenen Multiplikator für diesen Zeitpunkt. Weitere Informationen finden Sie unter dem Tipp weiter unten.
- Die Zwangsverschiebung kann entfernt und mithilfe des aktiven Bereichs erneut eingefügt werden. Diese Funktion ist in einer Vielzahl von Situationen hilfreich, in denen das Modell freigegeben werden muss, z. B. bei zeitabhängigen Randbedingungen. Um einen aktiven Bereich für diese Zwangsverschiebungen zu definieren, klicken Sie auf die Schaltfläche Daten neben dem Feld Aktiver Bereich.
- Die Kraft, die notwendig ist, um für den Knoten die Zwangsverschiebung durchzuführen, kann berechnet und ausgegeben werden. Weitere Informationen zum Aktivieren der Ausgabe für die Reaktionskraft finden Sie unter Steuern der Ausgabeergebnisse.
Die Geschwindigkei der Verschiebung oder Drehung wird durch die Lastkurve gesteuert, auf die sie angewendet wird. Die Verschiebung entspricht dem Integral der Geschwindigkeit (d = Integral V dt). Somit kann ein Graph der Verschiebung im Vergleich zur Zeit basierend auf der entsprechenden Geschwindigkeit berechnet werden. Die Daten für die Verschiebung im Vergleich zur Zeit werden in die Lastkurve eingegeben. Für eine konstante Geschwindigkeit:
d = d0 + V*t
wobei d0 die Anfangsposition, V die konstante Geschwindigkeit und t die Zeit ist. Beachten Sie, dass für eine konstante Geschwindigkeit zwei Punkte auf der Lastkurve ausreichen, da die Verschiebung linear ist und die Lastkurve in jedem Zeitschritt bei Bedarf linear interpoliert wird.
Um eine Beschleunigung während der Analyse zu simulieren, können Sie eine Lastkurve erstellen, die durch eine quadratische Gleichung definiert wird, die die Verschiebung des Knotens bei der Beschleunigung darstellt. Die Verschiebung entspricht dem zweiten Integral der Beschleunigung (d = doppeltes Integral A dt). Somit kann basierend auf der Beschleunigung ein Diagramm der Verschiebung im Vergleich zur Zeit berechnet und in die Lastkurve eingegeben werden. Für eine konstante Beschleunigung:
d = d0 + V0*t + 0.5*A*t2
wobei d0 die ursprüngliche Position, V0 die ursprüngliche Geschwindigkeit, A die konstante Geschwindigkeit und t die Zeit ist. Beachten Sie, dass für eine konstante Geschwindigkeit zwei Punkte auf der Lastkurve nicht ausreichen, da die Verschiebung zeitlich nicht linear ist, sodass eine lineare Interpolation zu keiner konstanten Beschleunigung führt. Um eine glatte, theoretische Beschleunigung zu erreichen, muss der Zeitschritt auf der Lastkurve kleiner als der kleinste Zeitschritt während der Analyse sein. Siehe Abbildung 1.
|
Verschiebung |
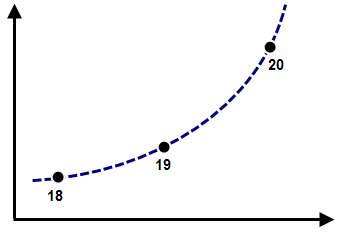
| (a) Die Verschiebungen in den Zeitschritten 18, 19 und 20 sind in der Lastkurve so definiert, dass sie der theoretischen Beschleunigung (gestrichelte Kurve) folgen. Wenn die Analyse die gleichen Zeitschritte verwendet, folgt die berechnete Verschiebung auch der theoretischen Beschleunigung. |
|
Verschiebung |
| (b) Wenn die Analyse den Zeitschritt reduziert, wird die Verschiebung an den dazwischen liegenden Schritten (Schritte 19 und 21) aus den Datenpunkten der Lastkurve linear interpoliert (Schritte 18, 20, 22). Eine lineare Verschiebung zwischen den Schritten 18 und 20 ergibt eine konstante Geschwindigkeit ohne Beschleunigung. Zwischen den Schritten 20 und 22 ergibt sich eine andere konstante Geschwindigkeit ohne Beschleunigung aus der Interpolation der Lastkurve. Eine plötzliche Änderung der Geschwindigkeit in Schritt 20 kann zu hohen Kräften und Konvergenzproblemen führen. |
| Abbildung 1: Verschiebungslastkurve zur Simulation der Beschleunigung |
Anwenden einer Zwangsverschiebung
Wenn Sie Knoten, Kanten, Flächen oder Bauteile ausgewählt haben, können Sie mit der rechten Maustaste in den Anzeigebereich klicken und im Kontextmenü Hinzufügen wählen. Wählen Sie den Befehl Zwangsverschiebungen.
Legen Sie fest, ob die Zwangsverschiebung eine Verschiebung oder eine Drehung auf den Knoten anwenden soll, indem Sie das entsprechende Optionsfeld im Abschnitt Typ aktivieren. Eine Drehung kann natürlich nur auf den Knoten eines Elements mit Rotations-Freiheitsgraden angewendet werden, z. B. ein Balken oder ein Gehäuseelement.
Geben Sie die Größe der Kraft, die auf die ausgewählten Objekte angewendet werden soll, in das Feld Betrag, und die Richtung der Last im Abschnitt Richtung ein. Wenn Sie das Optionsfeld Skalar X, Skalar Y oder Skalar Z auswählen, wird nur die Verschiebung oder Drehung in diese Richtung beschränkt; in den anderen Richtungen gibt es keine Beschränkungen für die Bewegung. Wenn Sie das Optionsfeld Vektor auswählen, wird die Verschiebung oder Drehung in alle drei Richtungen beschränkt. Wenn Sie beispielsweise eine Zwangsverschiebung des Betrags -1 Zoll hinzufügen und das Optionsfeld Skalar Y auswählen, ergibt die Analyse nur eine Reaktionskraft in der Y-Richtung. Der Knoten kann in X- oder Z-Richtung frei bewegt werden. Wenn Sie eine Zwangsverschiebung des Betrags 1 Zoll hinzufügen, das Optionsfeld Vektor auswählen und den Vektor (0,-1,0) definieren, ergibt die Analyse Reaktionskräfte in X-, Y- und Z-Richtung. Die Verschiebung in X- und Z-Richtung bleibt bei 0.
Geben Sie die Lastkurve, die zum Multiplizieren des Betrags verwendet wird, im Feld Lastfall/Lastkurve an. Klicken Sie auf die Schaltfläche Kurve, um im Lastkurven-Editor eine Lastkurve zu definieren, oder verwenden Sie das Dialogfeld Setup  Modell einrichten
Modell einrichten  Parameter
Parameter  Analyseparameter.
Analyseparameter.
Tipp
Da eine Zwangsverschiebung zu jedem Zeitpunkt während der Analyse aktiviert werden kann (unter Verwendung des Ursprungszeitpunkts des aktiven Bereichs, siehe weiter unten), wäre das Modell nicht stabil oder würde zu unvorhersagbaren Ergebnisse führen, wenn die Verschiebung zum Zeitpunkt T eine plötzliche Bewegung des Knotens von der vorherigen Position zu der Position wäre, die durch die Multiplikation des Betrags der Zwangsverschiebung mit dem Lastkurvenfaktor impliziert wird. Aus diesem Grund verwenden Zwangsverschiebungen nicht die typische Regel der Last zum Zeitpunkt T, die gleich dem Lastbetrag multipliziert mit dem Lastkurvenfaktor ist [D(T) = mag x LCM(T)]. Stattdessen entspricht die Bewegung während der Zeitschritt dem zugewiesenen Betrag der Zwangsverschiebung multipliziert mit der Änderung des Lastkurvenfaktors [ΔD(T) = mag x LCM(T)-LCM(T-1)]. Somit zeigen diese beiden Lastkurven unabhängig vom Betrag der Zwangsverschiebung an, dass sich der Knoten in den ersten beiden Sekunden der Analyse nicht bewegt (an seiner Position gehalten wird).
| Lastkurve 1 | ||
|---|---|---|
| Index | Zeit | Multiplikator |
| 1 | 0 | 5 |
| 2 | 2 | 5 |
| 3 | 2,5 | 6 |
| Lastkurve 2 | ||
|---|---|---|
| Index | Zeit | Multiplikator |
| 1 | 0 | 0 |
| 2 | 2 | 0 |
| 3 | 2,5 | 2 |
In dem Zeitraum zwischen 2 und 2,5 Sekunden ändert sich der Multiplikator der Lastkurve 1 um den Faktor 1 (= 6-5). Wenn der Betrag der Zwangsverschiebung, die der Lastkurve 1 folgen soll, 5 mm ist, bewegt sich der Knoten 5 mm in dem Zeitraum zwischen 2 und 2,5 Sekunden (= 5 mm x (6-5)).
Bei Verwendung der Lastkurve 2 ändert sich der Multiplikator um den Faktor 2 im Zeitraum zwischen 2 und 2,5 Sekunden Somit bewegt eine Zwangsverschiebung mit dem Betrag 5 mm den Knoten um eine Distanz von insgesamt 100 mm während dieses Intervalls (= 5 mm x (2-0)).
Weiteres Beispiel: Stellen Sie sich eine andere Zwangsverschiebung vor, die bei 2,25 Sekunden aktiviert wird (Ursprungszeitpunkt). Da die Bewegung in den ersten 2,25 Sekunden nicht beschränkt ist, nehmen wir eine X-Verschiebung zum Zeitpunkt 2,25 Sekunden von 0,3481 Zoll an. (Das liegt an den fiktiven Lasten im Modell.) Bei Verwendung der Lastkurve 1 mit dem Zwangsverschiebungsbetrag 0,1 Zoll bewegt sich der Knoten an die X-Pposition 0,3981 Zoll (= 0,3481 Zoll + 0,1 Zoll x (6-5,5), wobei 5,5 der Lastkurvenfaktor ist, der mit der Zeit 2,25 Sekunden interpoliert wurde).
Weisen Sie die Zwangsverschiebung einem aktiven Bereich zu, indem Sie die Zahl im Feld Aktiver Bereich festlegen. Beachten Sie, dass alle dem aktiven Bereich 1 zugewiesenen Zwangsverschiebungen den gleichen Ursprungs- und Beendigungszeitpunkt haben, alle dem aktiven Bereich 2 zugewiesenen Zwangsverschiebungen den gleichen Ursprungs- und Beendigungszeitpunkt haben usw. Dabei spielt es keine Rolle, wann die Zwangsverschiebung auf das Modell angewendet wurde, wenn mehrere Zwangsverschiebungen dem aktiven Bereich 1 zugewiesen werden, haben sie den gleichen Ursprungs- und Beendigungszeitpunkt.
Klicken Sie auf die Schaltfläche Daten neben dem Feld Aktiver Bereich, um den aktiven Bereich (die Zeitspanne) für die Zwangsverschiebung festzulegen. Die Index-Nummer oder die Zeile der Tabelle entspricht der Nummer des aktiven Bereichs, der der Verschiebung zugewiesen wurde. Geben Sie in der Spalte Ursprungszeitpunkt den Zeitpunkt an, ab dem die Zwangsverschiebung der Lastkurve folgen soll. Der Betrag und die Richtung der Zwangsverschiebung wird auf den Knoten ab der aktuellen Position zu diesem Zeitpunkt angewendet. Geben Sie in der Spalte Beendigungszeitpunkt den Zeitpunkt an, ab dem die Zwangsverschiebung deaktiviert werden soll (aus der Analyse entfernt wird). Geben Sie in der Spalte Aktivierungsindex einen Wert an, um die Zwangsverschiebung wieder zu aktivieren. Dieser Wert verweist auf eine andere Index-Zeile. Die Zwangsverschiebung wird zu dem Zeitpunkt, der in der Spalte Ursprungszeitpunkt für diesen Index angegeben ist, wieder aktiv.
 Zeit
Zeit 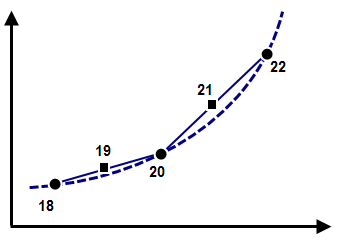 Zeit
Zeit