Les courbes et les surfaces NURBS n’existent pas dans le monde du dessin conventionnel. Elles ont été conçues spécialement pour la modélisation 3D sur ordinateur. Les courbes et les surfaces représentent des contours ou des formes dans un espace de modélisation 3D. Elles sont construites mathématiquement.
Les mathématiques à la base des NURBS sont complexes et, par conséquent, cette section est simplement une introduction à certains concepts NURBS, ayant pour but de vous aider à comprendre ce que vous créez et pourquoi les objets NURBS se comportent de telle façon. Pour une description complète des mathématiques et des algorithmes impliqués dans la modélisation NURBS, reportez-vous au livre The NURBS Book de Les Piegl et Wayne Tiller (New York : Springer, deuxième édition 1997).
Espace paramètres et définition
Le terme NURBS signifie Non-Uniform Rational B-Splines (splines B rationnelles non uniformes). Plus précisément :
- Non uniformes signifie que la portée d'un sommet de contrôle est variable. Cela peut être utile pour la modélisation de surfaces irrégulières.
- Rationnelles signifie que l'équation représentant la courbe ou la surface est exprimée en tant que rapport entre deux polynômes, et non de simple addition de ces éléments. L’équation rationnelle permet d'obtenir un meilleur modèle pour certaines courbes et surfaces importantes, en particulier pour les sections coniques, les cônes, les sphères, etc.
- Une spline-B (correspondant à spline de base) sert à construire une courbe interpolée entre trois points ou plus.
Les courbes Forme que vous créez à l'aide de l'outil Ligne et d'autres outils Forme sont des courbes de Bézier, type spécial de splines-B.
La propriété non uniforme des NURBS soulève un sujet important. Les objets NURBS sont générés mathématiquement et ils ont par conséquent un espace paramètre en plus de l'espace géométrique 3D dans lequel ils sont affichés. Un tableau de valeurs appelées noeuds spécifie la portée de chaque sommet de contrôle (CV) sur la courbe ou la surface. Les noeuds sont invisibles dans un espace 3D et ne peuvent pas être manipulés directement. Dans certains cas, leur comportement peut cependant affecter l'apparence visible d'un objet NURBS. Ces cas sont énumérés dans cette section. L’espace paramètre des courbes est à une dimension car, du point de vue topologique, elles n’ont qu'une dimension U, même si, d'un point de vue géométrique, elles existent dans l'espace 3D. Les surfaces, elles, ont deux dimensions dans l'espace de paramètres, appelées U et V.
La propriété essentielle des courbes et des surfaces NURBS est de ne pas être affectées par les transformations d'affinement géométrique standard (transformations) ni par les projections en perspective. Les CV contrôlent l'objet localement ; le déplacement d'un CV ou la modification de son poids n’affecte pas l'objet au-delà des CV voisins. (Vous pouvez néanmoins outrepasser cette règle à l'aide des commandes de Sélection adoucie.) En outre, le treillis de contrôle qui relie les CV entoure la surface. Il forme ce que l'on appelle une enveloppe convexe.
Degré et continuité
Toute courbe est affectée d'un degré. Le degré d'une courbe est l'exposant le plus élevé dans l'équation utilisée pour représenter cette courbe. Une équation linéaire est de degré 1 ; une équation quadratique est de degré 2. Les courbes NURBS sont généralement représentées par des équations cubiques et ont un degré de 3. Des degrés plus élevés sont possibles mais généralement inutiles.
Les courbes sont également définies par leur continuité. Une courbe continue est une courbe ininterrompue. Il existe différents niveaux de continuité. Une courbe avec un angle ou un point de rebroussement est C 0 continue , c'est-à-dire qu'elle est continue mais qu'elle n'a pas de dérivée au point de rebroussement. Une courbe ne comportant aucun point de rebroussement, mais dont la courbure change, est C 1 continue. Sa première dérivée est également continue, contrairement à la seconde. Une courbe dont la courbure est ininterrompue et fixe possède une continuité C 2 . Ses première et seconde dérivées sont également continues.

Niveaux de continuité de la courbe :
Gauche : C 0 , en raison de l'angle formé dans la partie supérieure
Milieu : C 1 , dans la partie supérieure, un demi-cercle en rejoint un autre de rayon inférieur
Droite : C 2 , la différence est subtile, mais le côté droit n'est pas un demi-cercle et il fusionne avec le côté gauche
Une courbe peut avoir des niveaux de continuité encore plus élevés mais ces trois niveaux sont adéquats pour la modélisation sur ordinateur. Généralement, il n'est pas possible de distinguer à l'oeil nu entre une courbe C2 continue et une courbe ayant une continuité plus grande.
La continuité et le degré sont liés. Une équation de degré 3 peut générer une courbe C 2 . C'est pourquoi les courbes à degré plus élevé ne sont généralement pas nécessaires dans la modélisation NURBS. De plus, les courbes d'un degré plus élevé étant numériquement moins stables, leur utilisation n’est pas recommandée.
Différents segments d'une courbe NURBS peuvent avoir différents niveaux de continuité. Vous pouvez, en particulier, réduire le niveau de continuité en plaçant les CV à la même position ou à des positions très rapprochées. Deux CV communs accentuent la courbure. Trois CV coïncidents produisent un sommet angulaire sur la surface. Cette propriété des courbes NURBS est appelée multiplicité. En effet, le ou les CV supplémentaires combinent leur influence à proximité de la courbe.
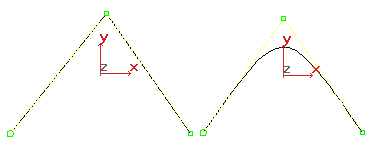
Effets de multiplicité : trois CV figurent au sommet du côté gauche et deux CV au sommet du côté droit.
Si vous éloignez un CV d'un autre, vous augmentez à nouveau le niveau de continuité de la courbe. La multiplicité s'applique également aux CV fondus. Les CV fondus provoquent une courbure plus prononcée ou créent un point de rebroussement sur la courbe. Là encore, cet effet est annulé si vous séparez les CV et que vous les éloignez l'un de l'autre.
Degré, continuité et multiplicité s'appliquent aux surfaces NURBS, ainsi qu'aux courbes.
Ajustement de courbes et de surfaces
Lorsque vous ajustez une courbe NURBS, vous lui ajoutez de nouveaux CV. Cette opération permet de mieux contrôler sa forme. Lors de l'affinement d'une courbe NURBS, 3ds Max conserve la courbure d'origine. En d’autres termes, la forme de la courbe ne change pas, mais les CV avoisinants s'éloignent du CV que vous ajoutez. Cela est dû à la multiplicité (si les CV avoisinants n’avaient pas bougé, l’ajout de CV supplémentaires rendrait la courbe plus aiguë). Pour éviter cet effet, , affinez d'abord la courbe, puis modifiez-la en transformant les CV ajoutés ou en ajustant leur poids.
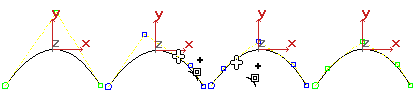
Affinement d'une courbe NURBS
Les surfaces NURBS ont essentiellement les mêmes propriétés que les courbes NURBS, étendues à deux dimensions (au lieu d'une) dans l'espace paramètre.
Définition de nouveaux paramètres pour les courbes et les surfaces CV
Lorsque vous affinez une courbe ou une surface NURBS, vous avez souvent intérêt à lui définir de nouveaux paramètres. La définition de nouveaux paramètres permet d'ajuster la partie paramétrable pour que la courbe (ou la surface) fonctionne correctement lorsque vous la modifiez dans les fenêtres. Pour définir de nouveaux paramètres, vous avez le choix entre deux procédés :
- Longueur de corde
La redéfinition des paramètres Longueur de corde espace les noeuds dans la partie paramétrable en se basant sur la racine carrée de la longueur de chaque segment de courbe.
- Uniforme
La définition uniforme de nouveaux paramètres espace les noeuds régulièrement. Un vecteur de noeud uniforme offre l'avantage de ne modifier la courbe ou la surface que localement lors de l'édition.
Avec les sous-objets courbe et surface CV, vous avez la possibilité d'effectuer une définition automatique des nouveaux paramètres au moment de l'édition.
Concepts relatifs aux courbes et surfaces de points
Vous pouvez manipuler des courbes et des surfaces de points, ou encore des courbes et des surfaces CV. Les points qui contrôlent ces objets doivent obligatoirement être situés sur la courbe ou la surface. Il n’y a ni treillis de contrôle ni contrôle du poids. Cette interface est donc plus simple et certains utilisateurs trouvent son utilisation plus facile. De plus, les objets basés sur les points vous donnent la possibilité de construire des courbes basées sur des points (contraints) dépendants, puis de les utiliser pour construire des surfaces dépendantes.
Les courbes et surfaces de points s'apparentent à des interfaces pour les courbes et les surfaces CV, objets NURBS par excellence. La représentation sous-jacente de la courbe ou de la surface continue d'être construite à l'aide de CV.
Vous pouvez également considérer une courbe ou une surface de points comme étant dépendante de ses points. Le bouton Convertir courbe vous permet de convertir une courbe ou une surface de points au format CV, ou vice versa.