3차원 시간 종속 연속성, Navier-Stokes 및 에너지 방정식은 층류뿐만 아니라 난류 흐름에 적용됩니다. 그러나 난류 흐름에 내재되어 있는 무한한 수의 시간 및 길이 축척으로 인해 이러한 방정식의 솔루션은 간단한 형상뿐만 아니라 경미한 시간 단계에 대해서도 수많은 유한 요소(106~108과 비슷함)를 필요로 합니다. 따라서 대부분의 실제 적용 분야에서 이 방식으로 흐름을 모형화하는 것은 적절하지 않습니다.
그러한 수많은 컴퓨터 리소스가 필요하지 않도록 하기 위해 축척 전반에 걸쳐 제어 pde의 평균이 계산됩니다. 평균을 구하는 데 여러 가지 축척 유형을 사용할 수 있습니다. Autodesk® CFD는 시간 평균 지배 방정식을 해석합니다.
시간 평균 방정식은 종속 변수를 평균값과 변동 값의 중첩으로 나타낼 수 있다고 가정하여 얻습니다. 여기서 변동은 평균에 대한 변동입니다. 예를 들어 x-속도 구성요소는 다음과 같이 작성할 수 있습니다.
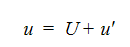
여기서 U는 평균 속도이고 u'는 해당 평균에 대한 변동입니다. 이 표현은 지배 방정식으로 대체되고, 시간이 흐름에 따라 방정식 자체에 대한 평균이 계산됩니다. 대문자가 평균값을 나타내고 소문자가 온도를 제외한 변동 값을 나타내는 표기법을 사용하여 평균을 구하는 지배 방정식을 다음과 같이 작성할 수 있습니다.
연속성 방정식
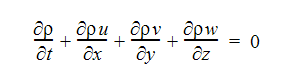
X-모멘텀 방정식
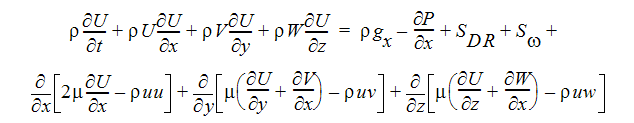
Y-모멘텀 방정식
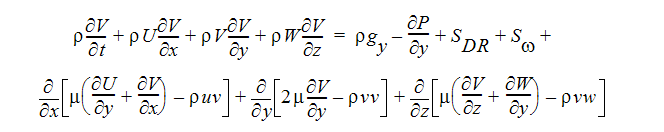
Z-모멘텀 방정식
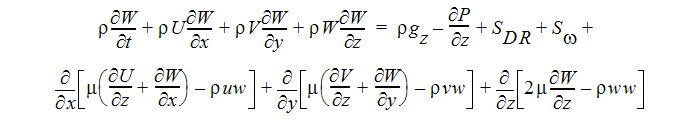
에너지 방정식
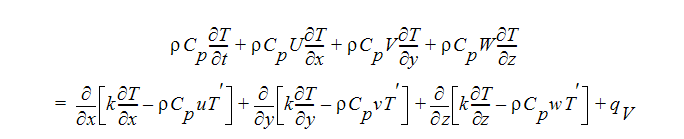
평균화 프로세스는 모멘텀과 에너지 방정식에서 다음과 같이 추가 항을 생성했습니다. 
uu, uv, uw, vv, vw, ww, CpuT', CpvT', CpwT'. 이러한 항은 비선형 관성 또는 이류 조건에서 구한 평균과 변동 수량을 조합한 것입니다. 모멘텀 방정식에서 추가 항을 레이놀즈 응력 항이라고 합니다.
이러한 항의 추가로 위의 방정식은 이제 14개의 미지수를 사용하여 5개 방정식을 나타냅니다. uu, uv, uw, vv, vw, ww, CpuT, CpvT, CpwT. 위 방정식의 모멘트를 사용하여 이러한 마지막 9개의 추가 항에 대해 추가 방정식을 파생할 수 있습니다. 하지만 이러한 방정식의 모멘트를 사용하는 프로세스는 여전히 더 많은 미지수를 사용합니다. 이 클로저 문제가 계속 반복될 수 있습니다. 특정 시점에서 방정식(및 새 항) 작성을 중지하고 추가 항을 "모형화"하는 방법을 찾도록 결정해야 합니다. 예를 들면 이러한 항을 이전 미지수에 다시 연결합니다. 클로저의 0차 수준에서 레이놀즈 응력 항은 종속 변수 U, V, W, T의 평균값에 연결됩니다.
널리 사용되는 하나의 0차 클로저는 Eddy 점도 및 Eddy 전도율을 정의하는 Boussinesq 근사입니다.
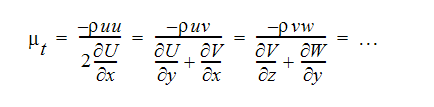
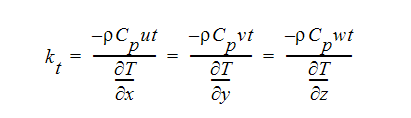
이러한 정의를 평균 방정식에 사용하는 경우 결과는 다음과 같습니다.
연속성 방정식
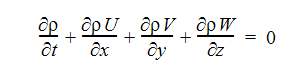
X-모멘텀 방정식
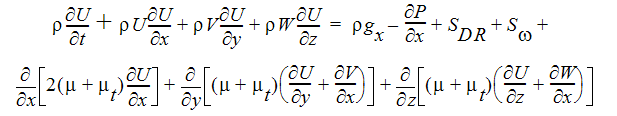
Y-모멘텀 방정식
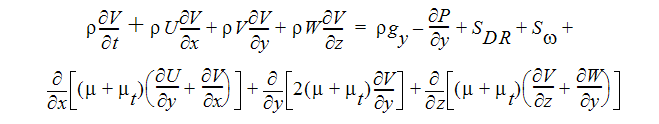
Z-모멘텀 방정식
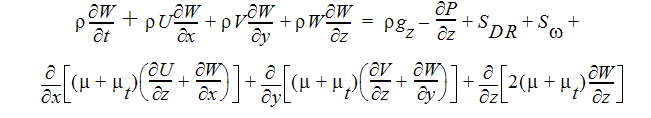
에너지 방정식
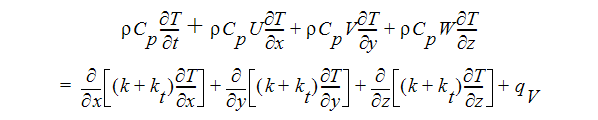
이 경우 Eddy 점도와 Eddy 전도율만 결정해야 합니다.