Autodesk® CFD에서 유한 요소 방법은 지배적인 편미분 방정식(pdes)을 일련의 대수 방정식으로 줄이는 데 사용됩니다. 이 방법에서 종속 변수는 작은 영역 또는 체적(요소)에 대해 다항식 형상 함수로 표현됩니다. 이러한 표현은 지배적인 pdes로 대체됩니다. 그런 다음 쉐이프 함수와 동일하도록 가중치 함수를 선택한 경우 요소에 대한 이러한 방정식의 가중 적분을 사용합니다. 결과는 모든 요소의 개별 점 또는 노드에서 종속 변수에 대한 일련의 대수 방정식입니다.
유선 상류 차분법 대류항 계산법
연속성 방정식을 제외한 지배 방정식은 솔루션 도메인을 통해 일부 수량(예: U, V, T)의 수송을 설명합니다. 지배 방정식의 수식은 다음과 같습니다.
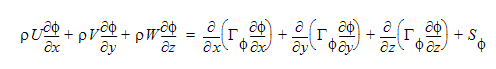
일반 스칼라 수송 방정식은 또한 소스 항이 없는 유사한 양식입니다.
위에서 설명한 유한 요소 방법은 확산 및 소스 항에서 직접 사용됩니다. 그러나 수치상 안정성을 위해 대류항 조건은 가중 적분 방법과 함께 상류 차분법 방법으로 취급됩니다. Autodesk® CFD에 사용된 4가지 상류 차분법 방법이 아래에 설명되어 있습니다.
ADV 1: 단조 유선 상류 차분법
- 수치상 안정적
- 1 < 순서 < 2
- 흐름 방향으로 정렬된 메쉬에 권장됨
- 흐름에 따라 정렬되지 않은 메쉬에 대해 수치상 분산됨
- 내부 장애물이 많은 형상에 대해 잘 작동함
- 돌출된 메쉬에 대해 잘 작동함
- 부품 표면에 지정된 분산 저항에 대해 잘 작동함
ADV 2: Petrov-Galerkin
- 중간 숫자 안정성(ADV 1보다 작음)
- 2 < 순서 < 3
- 임의 메쉬에 대한 숫자 분산은 더 작음
- 압력 구동 흐름에 권장됨
- 압축성 흐름에 권장됨
- 스칼라 및 에너지 운송 방정식에 기본적으로 사용됨
ADV 3: 플럭스 기반 계산법
- 대부분의 흐름에 대해 수치상 불안정함
- 순서 > 3
- 대류항 조건을 형성하는 데 여러 요소 업스트림 사용
- 비압축성 흐름에만 사용 가능함
- 이동 솔리드 해석에는 사용할 수 없음
- 끌기 또는 외부 흐름 문제에 맞게 특별히 조율됨
ADV 4: Min-Mod 계산법
- Petrov-Galerkin 변형
- 2 < 순서 < 3
- 중간 숫자 안정성(ADV 1보다 작음)
- 길고 좁은 덕트 흐름에 맞게 특수하게 조율됨
ADV 5: 수정 Petrov-Galerkin
- ADV 2의 보다 안정적인 버전
- ADV 2에 권장되는 모든 적용 분야 유형에 적합하지만 전반적으로 좀 더 효율적으로 결과를 생성함
- 재순환 및 2차 흐름에 이상적임
- 정확한 압력 강하 예측
- 자연 대류 안정성
- 압축성 유동 정확도 및 안정성
- 회전 및 모션 정확도 및 안정성
- 에너지 균형 안정성
- 체적에 지정된 분산 저항에 대한 정확도
대류항 조건에 대한 상류 차분법의 예로, 단조 유선(ADV 1)을 살펴보겠습니다. 이 상류 차분법 방법에서는 대류항 조건이 스트림 차원의 좌표로 변환됩니다.
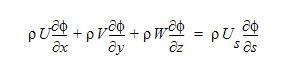
여기서 s가 스트림 차원의 좌표이고, U는 스트림 차원 좌표 방향의 속도 구성요소입니다. 순수한 대류항 문제에서 이 조건은 상수입니다. 이런 점을 고려하여 대류항 조건의 가중 적분을 다음과 같이 작성할 수 있습니다.
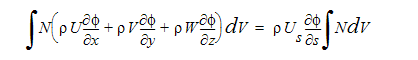
다른 대류항 계산법에서 쉐이프 함수는 요소에서 유선 곡률을 고려하도록 수정되었습니다.