热结果的某些命令与线性结果相同。以下是热分析所特有的命令。
计算的温度
（单位：度）这是当前显示的时间步（瞬态分析）或载荷工况（稳态分析）的结果温度。
初始温度
（单位：度）显示时间为 0 时的温度。该值不会随着时间步或载荷工况的变化而变化。对于稳态分析，该温度用于预测随温度变化材料的材料属性。
“初始温度”显示来自其他热模型的温度读数，默认节点温度或“初始温度”手动应用到 FEA 编辑器中的模型。“初始温度”不会显示外施载荷，例如控制温度或对流环境温度。
热通量
（单位：能量/长度^2/时间）如果激活，则显示内容取决于单元形心处的通量大小或指定的全局方向。形心处的热通量可使用傅立叶定律和节点温度计算得出。
通过面的热流率
（单位：能量/时间）如果激活，则显示内容取决于垂直于关联面的热流率。正值表示热通过该面流出单元；负值表示热通过该面流入单元。
形心处计算得出的热通量 (hfcg) 值可用于计算通过面的热流率 (H)，如下所示：
H =（垂直于面的 hfcg 分量）*（面的面积）。
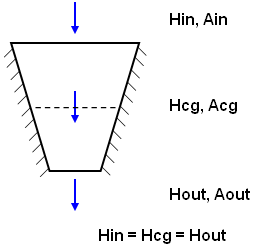
如果单元倾斜，或者单元面与热通量矢量不平行或不垂直，这可能会产生一些明显的差异。例如，假设热通过一个绝缘面的梯形单元稳态传递（请参见图 1(a)）。实际上，流入的热等于 (Hin) 等于流出的热 (Hout)。在 FEA 过程中，系统将计算得出形心处的热通量 (hfcg)，然后推导得出通过面的热流量。如图 1(b) 中所示，这将得出一个近似值，因此两个热流率值略有不同。
|
|
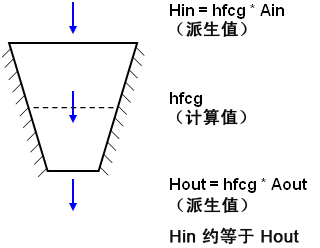
| (a) 在假想的模型中，无论是在入口面、形心 (cg)，还是出口处，通过任何区域的热流率 (H) 均相同。 | (b) 在 FEA 中，为形心计算得出的热通量 (hfcg) 用于计算通过面的热流率 (H)。如果 Ain 与 Aout 之和不等于 Acg，则流入的热不等于流出的热。 |
|
图 1：计算通过面的热流率 H = 热流率，A = 面积，hf = 热通量 |
|
此计算过程还会导致以下情况：通过面的热流率表明通过绝热墙的热量较少（请参见图 2）；与图 1 类似，从一个部件边界流出的热不等于流入另一个部件的热（请参见图 3）。这些效应是由于热流率的计算近似值而导致的。
Hout = hf n * 面的面积
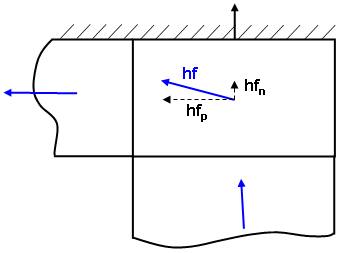
图 2：热通量投影的通过面的热流率
对于通过面的热流率，热通量矢量分解为平行 (hfp) 和垂直 (hfn) 于面的分量。较小的法向分量可能会违反绝热条件。如果壁面上的网格较小，则有助于尽量减少此类问题。或者，向绝热面添加一个小到可以忽略不计的对流载荷，并将“单元定义”对话框中的“热流计算”下拉菜单设置为“基于边界条件的线性”。
 |
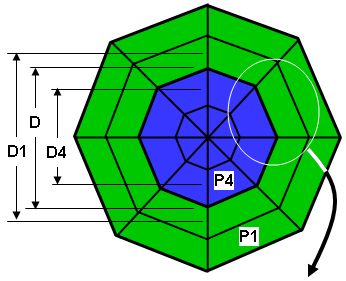(a) 双部件模型：部件 1（绿色）在外面，部件 4（蓝色）在里面。部件 1 中的内部单元形心直径为 D1。部件 4 中的外部单元形心直径为 D4。 |
 |
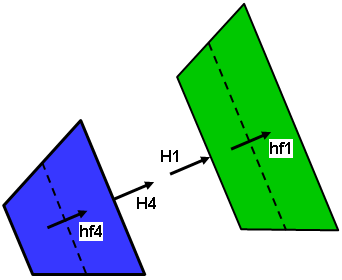(b) 两个模型单元的详细信息，为清楚起见，分别放大显示。热通量 hf4 和 hf1 通过温度分布计算得出。流出部件 4（蓝色）外部面的热流率与 H4 ~ hf4 * D 成比例。流入部件 1（绿色）内部面的热流率与 H1 ~ hf1 * D 成比例。由于直径 D 与用于计算热通量的形心直径 D1 和 D4 略有不同，因此，这两个热流率不会相同。 |
| 图 3：通过面的热流率示例 | |
对于内部面，从一个单元流出的热量和流入相邻单元的热量应当大小相等，方向相反。因此，平滑值应为零。在这种情况下，若要查看热流量的大小，请禁用“结果等值线” 
“设置” “平滑结果”。
若要合计通过一组面的热流量，请使用“查询结果” “查询” “当前结果”。选择面（“选择”“选择”“面”），然后将“摘要”下拉框更改为“总和”。
- 此外，您还可以选择表面来获取热流速结果，因此构建模型时，将面放置在唯一的表面上会比较方便。稍后，您可以在“结果”环境中选择此表面（“选择”“选择”“表面”），并使用“查询结果” “查询” “当前结果”合计这些值。
- 如果待合计的面具有外施载荷（如对流或辐射），请考虑使用浏览器中的“过滤模块”简化面的选择。（请参见浏览器函数页面。）
- 二维轴对称分析的“通过面的热流率”将得出旋转一周产生的总热流量（360 度 = 2*pi）。
对于块体单元，将显示外部面。若要查看内部面，您应使用“结果选项”“视图”“收缩单元”切换查看每个单元，然后使用“结果选项”“视图”“显示内部网格”显示内部面。
热流量精度
精度可用来亮显相邻单元之间结果的步长更改。在理想模型中，相邻单元之间的热通量将平滑变化。在使用单元离散模型的过程中，相邻单元之间的结果始终会呈现不同程度的变化。结果并非连续性。
在热分析中，精度取决于不同单元之间（跨单元边界）不连续的热通量大小。计算公式如下：
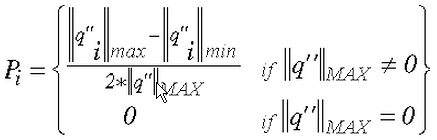
其中：
P i 是节点 i 处的精度，
max 是节点 i 处的最大热通量数值，通过查找相邻单元处最大值获得。
min 是节点 i 处的最小热通量数值，通过查找相邻单元处最小值获得。
MAX 是热通量数值的全局最大值。
根据上述公式，精度值的范围是 0 到 0.5（包括 0 和 0.5）。
如果模型部分隐藏，则精度计算取决于一组有限的节点和单元。属于单个单元的节点其精度为零。
液体分数
将瞬态热传递分析的任何部件设置为相变材料模型时，“液体分数”将出现在“结果等值线” “热流量” “相变”中。值为 1 表示节点是液体，值为 0 表示节点是固体，值介于 1 和 0 之间表示融化或冻结状态以及哪一质量分数是液体。如果节点所属的部件未设置为相变材料模型，则节点不会通过结果着色。