无
选择此选项将从模型移除结果等值线并为着色和网格线使用默认颜色。
位移
此选项将对模型进行着色以显示位移。可用的命令如下：
- 数值：将显示设置为基于位移数值。此值将始终为正值。数值为节点移动的总距离。mag = sqrt[(dX)^2 + (dY)^2 + (dZ)^2]
- X：将显示设置为基于位移矢量与 X 方向单位矢量的点积。此项显示 X 方向的总位移分量。
- Y：将显示设置为基于位移矢量与 Y 方向单位矢量的点积。此项显示 Y 方向的总位移分量。
- Z：将显示设置为基于位移矢量与 Z 方向单位矢量的点积。此项显示 Z 方向的总位移分量。
- 矢量图：将显示设置为基于位移的数值，将结果显示为在每个节点处绘制的矢量（箭头）。箭头的长度和颜色代表位移的数值，箭头的方向代表位移的矢量方向。使用“显示选项：绘图设置：矢量图”选项卡可调整箭头尺寸。
转动
此选项将为模型着色以显示各节点处的转动。此结果将仅适用于可抵抗转动的单元节点。例如，块体单元上的节点仅具有三个可用的平动自由度。因此，将不会计算转动位移。梁单元上的节点可以抵抗全部三个方向的转动。板单元上的节点可以抵抗两个平面内方向的转动。可用的命令如下：
- 数值：将显示设置为基于转动位移的数值。此值将始终为正值。数值为节点移动的总旋度。mag = sqrt[(rX)^2 + (rY)^2 + (rZ)^2]
- X：将显示设置为基于转动矢量与 X 方向单位矢量的点积。此项显示关于 X 轴的总旋度分量。
- Y：将显示设置为基于转动矢量与 Y 方向单位矢量的点积。此项显示关于 Y 轴的总旋度分量。
- Z：将显示设置为基于转动矢量与 Z 方向单位矢量的点积。此项显示关于 Z 轴的总旋度分量。
在大变形分析（MES 或非线性分析）中，如果涉及多个转动，需要谨慎解读转动结果。转动结果包含完整的运动历史记录，因此与路径相关。请参见下图示例。（位移结果与路径无关。）
L 形梁的起点位于 XZ 平面。
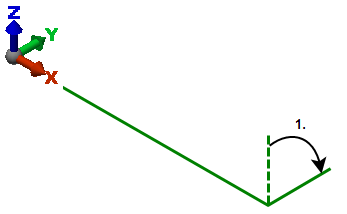
1. 梁绕 X 轴转动 -90 度。
2. 梁绕 Z 轴转动 90 度。
3. 梁绕 Y 轴转动 180 度。
4. 梁绕 Z 轴转动 -90 度。
将最终位置与初始位置进行比较，能看出最终转动结果可以简化为绕 X 轴转动 +90 度并绕 Y 轴和 Z 轴转动 0 度。在大变形分析中，结果为绕 X 轴转动 -90 度、绕 Y 轴转动 180 度和绕 Z 轴转动 0 度。
由于位移结果与路径无关，因此最终位移结果是在 X 方向为 0、在 Y 和 Z 方向为 -L，其中 L 是短边的长度。
在上面的示例中，是否使用“大刚体转动”选项（在梁单元的“单元定义”对话框中设置）决定是否能够实现梁方向的可视化。仅当使用“大刚体转动”时，轴 2 和 3 的方向才是准确的。
标准化位移和转动
- 固有频率（模态）
应力
提供多种分析方法以帮助用户确定模型的适用性。“结果”环境提供局部坐标中的原始应力和通过这些原始应力推导的多个量，因此用户可通过“结果”环境对这些方法进行访问。推导量包括 von Mises 和 Tresca 准则、最大和最小主应力以及单元特定输出。由于分析结果的准确性取决于网格结构和 FEA 参数应用，因此“结果”环境将提供共享节点处的精度估算。此精度值可以帮助用户确定模型的适用性。
计算
软件使用“节点应力”方法来计算应力估算。利用外插方案，与通过单元内应力推导的计算相比，使用节点应力的计算通常可以提供更高的精度。显示节点处的应力可以生成更适合、更逼真的载荷模型表示，因为节点处的应力值比为整个单元计算的应力值有用。
计算得出的单元应力将在高斯点处生成应力信息。高斯点是数值积分点，这些点上的有限元解和理论解最接近。旧方法会将这些应力平均到二维单元的中心或面和三维单元的质心，且可能在相邻单元之间显示相对较大的差异。因为有限元解是连续函数的近似值，因此这些位置的结果可能过于粗糙，无法提供应力作用下模型行为的精确图片。
计算各个节点处的应力可以更正此问题。使用“局部最小二乘法”方法，可通过高斯点的应力推导相关节点的应力。如果节点位于正在进行分析的部件表面或边上，则准确地估算节点处的应力尤其重要，因为这些节点通常会与模型的重要区域重合。还提供不同单元之间共享节点处的精度信息。
当显示模型的表面时，将计算定义表面的网格的每个单元上节点处的强度或应力，并将相应的显示值指定给该点。接下来，将检查用于显示表面的比例，并根据每个点的计算值为该点选择适当的颜色和着色。之后，将根据使用的显示方法重新绘制模型并对模型表面进行着色。“结果”环境提供可视化选项（如平滑）以用于控制模型的显示方式。这样可使用户以最有效的方式查看模型。
von mises
此命令会将结果显示设置为等效的 von Mises 应力以供显示或数据输出。von Mises 应力可以针对具有面积（二维、板等）和体积（块体）的单元类型显示。
使用的方程为：
其中 Sx、Sy 和 Sz 是整体方向上的轴应力，Sxy、Syz 和 Sxz 是剪切应力。根据主应力 S1、S2 和 S3：
注意，方程中的 von Mises 值始终为正值。
Tresca*2
Tresca*2 应力可以针对具有面积（二维、板等）和体积（块体）的单元类型显示。此方法会从以下应力张量中提取最大剪切应力。Tresca 方程为：
其中 S1、S2 和 S3 是主应力。报告的值为最大剪切应力的两倍。因此，当报告的 Tresca*2 值达到屈服应力时会发生屈服。根据定义，Tresca 应力始终为正值。相关图解，请参见莫尔圆。Tresca*2 也称为应力强度。
最小主应力
此命令会将结果显示设置为计算最小主应力 (S3) 以供显示或数据输出。主应力可以针对具有面积（二维、板等）和体积（块体）的单元类型显示。正值 (+) 表示拉伸，负值 (-) 表示压缩。相关图解，请参见莫尔圆。
最小主应力方向
此命令将显示各单元中最小主应力的方向矢量图。将平均单元各节点处的张量，并在单元质心处绘制此平均张量的最小主应力方向。如果选择某个单元并选择“查询结果”
“查询” “当前结果”，则将显示此矢量的分量。
中间主应力
此命令会将结果显示设置为计算中间主应力 (S2) 以供显示或数据输出。这是最小主应力和最大主应力的法线方向上的应力。主应力可以针对具有面积（二维、板等）和体积（块体）的单元类型显示。正值 (+) 表示拉伸，负值 (-) 表示压缩。
中间主应力方向
此命令将显示各单元中中间主应力的方向矢量图。将平均单元各节点处的张量，并在单元质心处绘制此平均张量的中间主应力方向。如果选择某个单元并选择“查询结果”“查询”“当前结果”，则将显示此矢量的分量。
最大主应力
此命令会将结果显示设置为计算最大主应力 (S1) 以供显示或数据输出。主应力可以针对具有面积（二维、板等）和体积（块体）的单元类型显示。正值 (+) 表示拉伸，负值 (-) 表示压缩。相关图解，请参见莫尔圆。
最大主应力方向
此命令将显示各单元中最大主应力的方向矢量图。将平均单元各节点处的张量，并在单元质心处绘制此平均张量的最大主应力方向。如果选择某个单元并选择“查询结果”“查询”“当前结果”，则将显示此矢量的分量。
张量
此命令将显示选定方向的应力分量。从技术上讲，它将双点积与应力张量或局部应力分量结合使用。应力张量可以针对具有面积（二维、板等）和体积（块体）的单元类型显示。
如果“结果等值线”“设置”“使用单元-局部结果”未处于活动状态，则可以在下列全局应力之间进行选择。如果此选项处于活动状态，则以下选项将显示各个描述中提到的局部应力张量。
对于具有局部轴的单元，平滑（平均）应力可能没有意义，尤其是相邻单元之间的局部轴方向不固定时。仅当从一个单元到另一个单元的局部轴方向不变时，平滑的应力张量值才有意义。
- 1) XX：显示整体 X 方向上的法向应力的应力张量分量。正值 (+) 表示拉伸；负值 (-) 表示压缩。如果“结果等值线”“设置”“使用单元-局部结果”处于活动状态，则将显示局部 1-1 应力张量。
- 2) YY：显示整体 Y 方向上的法向应力的应力张量分量。正值 (+) 表示拉伸；负值 (-) 表示压缩。如果“结果等值线”“设置”“使用单元-局部结果”处于活动状态，则将显示局部 2-2 应力张量。
- 3) ZZ：显示整体 Z 方向上的法向应力的应力张量分量。正值 (+) 表示拉伸；负值 (-) 表示压缩。如果“结果等值线”“设置”“使用单元-局部结果”处于活动状态，则将显示局部 3-3 应力张量。
- 4) XY：显示整体 XY 方向上的剪切应力的应力张量分量。（X 表示面的法向方向，Y 表示剪切应力的方向。）如果“结果等值线”“设置”“使用单元-局部结果”处于活动状态，则将显示局部 1-2 应力张量。
- 5) YZ：显示整体 YZ 方向上的剪切应力的应力张量分量。（Y 表示面的法向方向，Z 表示剪切应力的方向。）如果“结果等值线”“设置”“使用单元-局部结果”处于活动状态，则将显示局部 2-3 应力张量。
- 6) ZX：显示整体 ZX 方向上的剪切应力的应力张量分量。（Z 表示面的法向方向，X 表示剪切应力的方向。）如果“结果等值线”“设置”“使用单元-局部结果”处于活动状态，则将显示局部 3-1 应力张量。
梁和桁架
此命令将显示线性和非线性桁架单元、线性和非线性梁单元以及非线性管道单元的应力。可用的结果如下所示：
- 对于产生塑性变形的梁单元非线性分析，这些命令显示的结果仅通过屈服强度进行了部分更正。每个应力（轴应力、局部 2 轴的弯曲应力和局部 3 轴的弯曲应力）均会封口或（如有必要）仅限于屈服应力。然后，最坏应力将这三个结果加在一起。
- 要获得更精确的应力结果，请激活梁“单元定义”上的“二进制应力和应变输出”选项，再运行分析。然后，在“结果”环境中使用“查询结果”“查询”“详细梁应力”和“查询结果”“查询”“详细梁应变”查看结果。
- 轴应力(局部 1 方向)：显示轴应力。此项通过轴向力除以横截面面积计算。正值表示拉伸应力，负值表示压缩应力。
- 局部 2 方向的弯曲应力：显示因局部 2 轴相关弯曲力矩造成的梁单元中的弯曲应力。此项通过轴 2 相关弯曲力矩除以局部轴 2 相关截面模量计算。局部 2 轴通过 k 节点并垂直于梁。（由于桁架单元没有弯曲性能，因此此菜单项不会应用于桁架单元。）
- 局部 3 方向的弯曲应力：显示因局部 3 轴相关弯曲力矩造成的梁单元中的弯曲应力。此项通过轴 3 相关弯曲力矩除以局部轴 3 相关截面模量计算。局部轴 3 为局部轴 1 和 2 的矢量乘积。（由于桁架单元没有弯曲性能，因此此菜单项不会应用于桁架单元。）
- 最不利：在某个角，轴 2 相关轴应力、弯曲应力和轴 3 相关弯曲应力的组合生成最大绝对值。这是梁中的最不利应力。对于线性应力，正值 (+) 表示梁处于轴向拉伸状态，负值 (-) 表示梁处于轴向压缩状态。从数学角度来说，
最不利 = (P/A 的符号)(ABS(P/A)+ABS(M2/S2)+ABS(M3/S3))
应力分析（线性和非线性）假设横截面对称（由于 S2 和 S3 仅有一个输入或计算得出的值）。因此，从数学角度来说，最不利的应力可能出现在非对称梁中不存在的位置，如图 1 中的左下角或左上角。
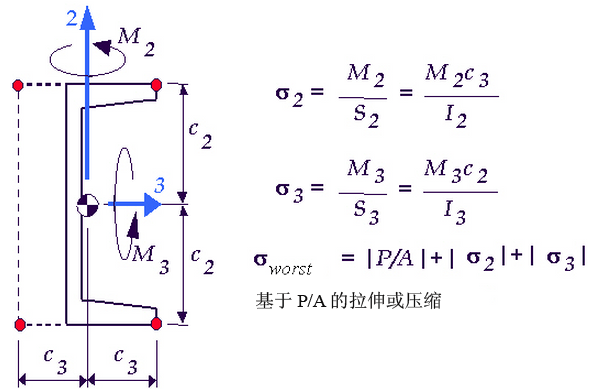
图 1：非对称梁中的应力结果
由于假设 C2 和 C3 相等（根据 S3 和 S2 仅一个输入），因此可能在不存在的位置报告最不利应力。
使用“结果选项”“视图”“单元方向”可显示梁单元的局部 1、2 或 3 轴。
复合
失效索引
此命令将显示与“单元定义”对话框中设置的平面内复合材料失效准则对应的结果（Tsai-Wu、最大应力或最大应变）。
建议禁用平滑（“结果等值线”“设置”“平滑结果””）以查看每个单元中的实际失效准则值（而不是相邻单元之间的平滑值或平均值）。
可以使用“结果等值线”“应力”“复合材料”“选项”控制正在查看结果的层。还可以使用此命令选择查看“最不利”结果。
对于最大应力和最大应变准则，请先根据层的顶面和底面考虑以下安全系数：
最大应力 - 安全系数：
、
、
、
和 
其中 σ 是方向 1 或 2 上计算得出的法向应力，X 和 Y 是方向 1 和 2 上的许用应力（与计算得出的应力匹配的压缩或拉伸应力），τ12 是计算得出的剪切应力，S 允许剪切应力。
最大应变 - 安全系数：
、
、
、
和 
其中 ε 是方向 1 或 2 上计算得出的法向应变，T 是方向 1 和 2 上的相应许用应变（与计算得出的应变匹配的压缩或拉伸应变），γ12 是计算得出的剪切应变，S 允许剪切应变。
然后，显示的结果如下所示：
| 最大应力和最大应变的失效索引 | |
|---|---|
| 线性应力 | 非线性应力 |
| 计算 1/安全系数的值 | 计算安全系数的值 |
| 绘制最大值 | 绘制最小值 |
| 值大于 1 表示失效 | 值小于 1 表示失效 |
对于 Tsai-Wu 失效准则，请先考虑值 F：
其中
σ 和 τ 是计算得出的法向应力和剪切应力，而所有其他值为材料输入。
然后，显示的结果如下所示：
| Tsai-Wu 的失效索引 | |
|---|---|
| 线性应力 | 非线性应力 |
| 绘制值 F | 绘制值 1/F |
| 值大于 1 表示失效 | 值小于 1 表示失效 |
平面外失效
如果要使用具有最大应力失效准则的厚型复合材料单元，则此选项将可用于查看核心层的厚度方向（平面外方向）的失效准则结果。绘制的结果是以下各项的最大值：
、
和 
其中 σcore 是计算得出的内核中的法向应力（方向 3），Zc 是允许的核心压碎应力，τ 是计算得出的剪切应力，S 是允许的横向剪切应力。
大于 1 的值表示失效。
应变
之前介绍的大多数应力结果公式可用于显示模型中的应变结果；将说明和公式中的应力替换成应变即可。在这些情况下，以下说明包含指向等效页面的链接。以下将详细介绍与等效应力命令有显著差别的应变结果命令。
- von Mises：使用 von Mises 方程显示等效应变。有关更多详细信息，请参见 von Mises 应力讨论。
- Tresca*2：使用两倍的 Tresca 应变显示等效应变。有关更多详细信息，请参见 Tresca 应力讨论。
- 最小主应变：显示最小主应变。有关更多详细信息，请参见最小主应力讨论。
- 最大主应变：显示最大主应变。有关更多详细信息，请参见最大主应力讨论。
- 张量：显示选定方向的应变分量。对于线性材料模型的静态应力分析，可以以单元、整体或柱坐标查看应变（与应力一样）。 注： 对于 MES 分析，可提供“工程”应变结果，而不是应变张量结果。以下矩阵表示工程应变 (MES)：而张量应变（线性）矩阵为：
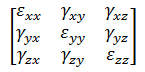
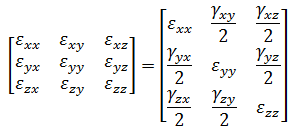
- 梁和桁架梁和桁架单元的应变菜单包含以下选项。
- 轴向：显示载荷作用下沿梁/桁架的轴产生的轴向应变。拉伸应变被视为正值。
- 绕轴 2 弯曲：显示轴 2 相关力矩造成的最大纤维应变。这仅适用于梁。拉伸应变被视为正值。
- 绕轴 3 弯曲：显示轴 3 相关力矩造成的最大纤维应变。这仅适用于梁。拉伸应变被视为正值。
- 最不利组合：对于梁单元，显示轴向、轴 2 相关弯曲和轴 3 相关弯曲的最不利组合。从数学角度来说，
最不利 = (P/A 的符号)(ABS(P/A)+ABS(轴 2 相关应变)+ABS(轴 3 相关应变))
对于桁架单元，最不利应变等于轴向应变 (P/A)。
应变能密度
如果选择此命令，模型将按照应变能密度着色。单元的应变能定义为载荷作用下单元吸收的能量。该能量可以基于单位体积计算：
。
标准化应力和应变
- 固有频率（模态）
这些结果的唯一用途是显示模型中的相关应力和应变分布。即用户可以找到最大或最小应力和应变的区域，但无法仅使用模态分析量化结果。因为结果不会缩放至任何特定激励，因此绝对应力和应变值没有意义。
Autodesk Moldflow 结果
如果适用，则可将 Autodesk Simulation Mechanical 模型导出到 Autodesk Moldflow Adviser 或 Insight 以模拟注塑成型过程。Moldflow 模拟完成后，可在 Autodesk simulation Mechanical 的“结果”环境中对其他结果进行可视化。在功能区中“结果等值线”选项卡上的“Moldflow 结果”面板中选择这些结果。
在“线性”分析类型中，“Moldflow 结果”仅适用于“线性材料模型静态应力”。“Moldflow 结果”也适用于所有“非线性”结构分析，“非线性材料固有频率(模态)”除外。提供以下结果：
- “残余应力张量”下拉菜单用于选择六个残余应力张量分量（XX、YY、ZZ、XY、YZ 和 ZX）之一。这些分量基于 Moldflow 模拟的型腔内部件应力（完成成型过程后）。这些是仍具有模具约束的应力，部件脱离模具后，这些残余应力将导致部件变形。
- “CTE 张量”下拉菜单用于选择六个方向的“热膨胀系数”张量分量（XX、YY、ZZ、XY、YZ 和 ZX）。这些是 Moldflow 分析中基于层的 CTE 结果。六个 CTE 张量分量并非适用于所有材料。仅定义为具有各向异性热属性的材料才会包含六个 CTE 分量。
单元位移
“单元受力”和“力矩”下的结果主要是线单元的结果：桁架、间隙、梁、边界单元等。
- 拉伸：此命令将基于长度的改变为间隙、边界、桁架或弹簧单元着色。对于间隙、桁架和弹簧单元，正值表示拉伸。对于边界单元，正值表示单元处于压缩状态。
- 扭曲：此命令将基于单元的转动对边界单元进行着色。方向遵循从单元连接节点到自由端的右手法则。
单元受力和力矩
“单元受力”和“力矩”下的结果主要是线单元的结果：桁架、间隙、梁、边界单元等。
- 轴向力：显示所有类型的线单元的轴向力（局部 1 方向）：桁架、梁、弹簧、间隙和边界单元。对于桁架、弹簧和间隙单元，正值表示拉伸，负值表示压缩。对于边界单元，正值表示单元处于压缩状态，负值表示单元处于拉伸状态。对于梁单元，请参见下方的“梁单元的局部力和力矩方向”段落。
- 轴 2 的剪切力：显示梁单元局部 2 方向的剪切力。
- 轴 3 的剪切力：显示梁单元局部 3 方向的剪切力。
- 扭矩：显示梁单元（局部轴 1 相关力矩）和转动边界单元中的扭矩。对于边界单元，单元中模型连接节点处的扭矩方向遵循从单元连接节点到自由端的右手法则。对于梁单元，请参见下方的“梁单元的局部力和力矩方向”段落。
- 轴 2 相关力矩：显示梁单元的局部轴 2 相关力矩。
- 轴 3 相关力矩：显示梁单元的局部轴 3 相关力矩。
- 板弯曲力矩：该项处于活动状态时，弯曲力矩张量
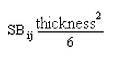
将用于所有板应力计算。弯曲力矩张量是分布力矩（线力矩、单位长度的力矩）。最容易解释的结果来自“结果等值线”“应力”“张量”。将执行 von Mises、Tresca、最大和最小主应力的数学计算，但会提供等效于弯曲应力值乘以
的结果。
梁单元的局部力和力矩方向：
| 分量 | 结构梁 |
|---|---|
| 局部 1 力 | 正 (+) 值表示拉伸，负 (-) 值表示压缩。 |
| 局部 2 力 |
|
| 局部 3 力 |
|
| 局部 1 力矩 |
|
| 局部 2 力矩 |
|
| 局部 3 力矩 |
|
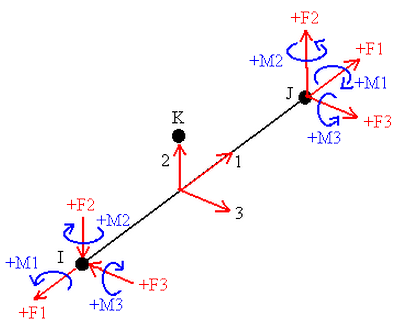
图 2：梁单元的局部力和力矩方向
功率谱密度
如果执行随机振动分析时选中用于输出功率谱密度的选项，“结果”将包含“功率谱密度”条目。（有关此选项的详细信息，请参见随机振动页面。）功率谱密度图绘制步骤如下：
- 显示模型所有类型的结果，例如位移或应力。
- 选择功率谱密度适用的一个或多个节点，单击鼠标右键，然后选择“图形表示值”。
- 创建完图形后，选择“查询结果”“图形”“功率谱密度”，显示以下结果之一：
- X 位移：显示 X 位移的功率谱密度。
- Y 位移：显示 Y 位移的功率谱密度。
- Z 位移：显示 Z 位移的功率谱密度。
- X 转动：显示 X 转动的功率谱密度。
- Y 转动：显示 Y 转动的功率谱密度。
- Z 转动：显示 Z 转动的功率谱密度。
请记住，这些是相对于支架的结果。它们参考有关输入激励的功率谱密度。
如果绘制了多个节点，则需要为每个节点激活功率谱密度，一次激活一个。在浏览器中的所需节点上单击鼠标右键，选择“设置为活动”，然后尝试显示功率谱结果。（有关常规说明，请参见分析的图形结果页面。）
反作用力
此命令将显示内部力和反作用力。要显示的结果类型如下所示：
- 内部力：在线性分析中，此菜单将显示每个节点处的内部力反作用。它不是支承反作用力；请使用“残余力”命令。可以显示反作用力的数值，也可以沿整体轴显示各个分量。
- 指定力：显示应用于每个节点的力。可以显示指定力的数值，也可以沿整体轴显示各个分量。
- 反作用力(负)：显示每个节点处的残余力（应用的力和反作用力之和）。大多数工程师认为该力是支承反作用力，唯一区别是残余力是模型对周围对象的作用力。残余力和支承反作用力大小相等方向相反。可以显示残余力的数值，也可以沿整体轴显示各个分量。
在 MES/非线性分析中，此菜单显示每个节点处的反作用力。边界条件、规定位移、冲撞壁面和面面接触处的结果非零。
- 内部力矩：在线性分析中，此菜单将显示每个节点处的内部力矩反作用。它不是支承反作用力；请使用“残余力矩”命令。可以显示反作用力矩的数值，也可以沿整体轴显示各个分量。
- 指定力矩：显示应用于每个节点的力矩。可以显示指定力矩的数值，也可以沿整体轴显示各个分量。
- 反作用力矩(负)：显示每个节点处的残余力矩（指定力矩和反作用力矩之和）。大多数工程师认为该力是支承反作用力，唯一区别是残余力矩是模型对周围对象的作用力矩。残余力矩和支承反作用力大小相等方向相反。可以显示残余力的数值，也可以沿整体轴显示各个分量。
在 MES/非线性分析中，此菜单显示每个节点处的反作用力矩。边界条件和规定转动处的结果非零。
每个结果类型具有以下选项：
- 数值：根据结果的数值对模型进行着色。
- X：根据结果的 X 分量对模型进行着色。
- Y：根据结果的 Y 分量对模型进行着色。
- Z：根据结果的 Z 分量对模型进行着色。
- 矢量图：在每个节点处将结果显示为箭头。箭头的长度和颜色代表结果的数值，箭头的方向代表结果的矢量方向。 注： 通过智能粘合连接的节点处的反作用力/力矩和残余力/力矩非零。（部件之间的边界处的这些结果通常为 0）。
Von Mises 精度
精度方法用于亮显一个单元到下一单元的结果阶梯式变化。在理想模型中，相邻单元之间的应力将平滑变化。在将模型解剖为多个单元的过程中，一个单元到下一单元的结果之间始终存在一些变化。结果不连续。
例如，在应力模型中，具有共享节点的单元将独立预测节点处的应力，因此独立的应力计算将为基于 Von Mises 应力的模型提供精度估算。指定节点处的精度值计算方法如下：
根据定义，精度的变化范围为 0（最佳）到 0.5（最差）。未在两个或更多单元之间共享的节点将仅具有一个应力估算，因此精度索引为 0。
示例 1：
如果模型中的最大 von Mises 应力为 200，则以下节点（节点最多连接 3 个单元）处的精度如下所示：
| 节点编号 | 范式等效应力 | 精度值 | 备注 | ||
|---|---|---|---|---|---|
| 值 1 | 值 2 | 值 3 | |||
| 17 | 20 | -- | -- | .0 | 单个单元节点 |
| 23 | 20 | 40 | 25 | .05 | .5(40-20)/200 |
| 36 | 150 | 120 | 200 | .20 | .5(200-120)/200 |
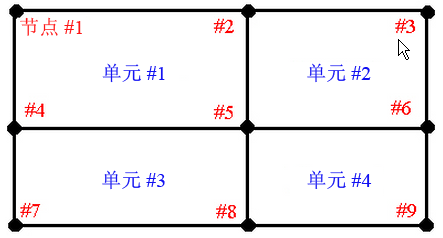
示例 2：
根据下图显示的节点 5 周围的四个单元和以下应力：
| 单元编号 | 节点编号 | 范式等效应力 |
|---|---|---|
| 1 | 5 | 20,000 |
| 2 | 5 | 15,000 |
| 3 | 5 | 19,000 |
| 4 | 5 | 10,000 |
如果模型中的最大应力为 25,000（例如在节点 9 处），则节点 5 处的精度为
节点 5 的精度 = 0.5(20,000 - 10,000)/25,000 = 0.20
无法保证实际应力会位于指定范围内。实际应力所在的范围取决于模型网格划分好坏、实际零件的建模好坏以及其他因素。不应考虑小于指定精度范围的差异。例如，如果精度为 0.1 且最大应力为 200，则可以忽略小于 20 个应力单位的差异。
外施载荷
选择此选项将显示模型及其输入载荷。适用于结构分析的载荷为温度和电压。
- 对于线性应力:
- “结果等值线”“其他结果”“外施载荷”“温度”命令始终可用。
- 将为模型文件、稳态热传递或瞬态热传递的“分析参数”中指定的所有类型的温度载荷显示等值线。
- 温度对分析的影响还取决于无应力参考温度和热乘子。这些贡献因子不会显示在温度等值线中。
- “结果等值线”
- 对于机械运动仿真/非线性应力:
- 仅当将“节点温度源”指定给“分析参数”中的模型时，“结果等值线”“其他结果”“外施载荷”“温度”命令才可用。
- 将仅为模型文件中的温度载荷显示等值线。无法绘制稳态热传递或瞬态热传递的温度等值线。
- 温度造成的影响还取决于无应力参考温度和载荷曲线乘子。载荷曲线乘子的影响将通过温度等值线显示。
- 仅当将“节点温度源”指定给“分析参数”中的模型时，“结果等值线”
单元属性
此命令将根据单元的形状对模型进行着色。大多数的命令仅适用于面积和体积单元：二维、板、块体单元等。
以下各选项将根据选定条目对模型进行着色。
- 体积：如果必须在模型上执行“分析”“分析”“重量和重心”，则选择“结果等值线”“其他结果”“单元属性”“体积”命令将显示每个单元的体积。如果已在“查询：结果”对话框中计算了加权的结果摘要，则将自动运行“重量和重心”计算器。
- 扭曲角：将显示四边形（4 节点）单元或实体单元的 4 节点面的扭曲量。有三种方法可用于计算扭曲角。
- 最小折叠方法或最大折叠方法：如果选择其中一个命令，则将计算两个四边形折叠角并使用最小或最大折叠角。四边形折叠角通过将四边形分割成两个三角形获得（添加两个可能的对角线之一）。折叠角是这两个三角形的平面法线之间的角度。
- 中面方法：在此情况中，中面角度的正弦值等于中面上方任意端节点的高度除以 1/2 最短边的长度。中面是包含边直线的所有 4 个中点的平面。每个节点到此平面的距离都相等。扭曲角的计算公式是中面角度乘以 2*(2) 的平方根，这样它将与以小角度弯曲的正方形的折叠角相当。由于使用中面中的角度而不是总折叠角，因此有系数 2。由于以半侧而不是以半对角线分割，因此有系数 (2) 的平方根。
- 节点角：如果处于活动状态，则将基于单元任意面的最大节点（内部）角显示单元。
- 长宽比：如果处于活动状态，则将基于长宽比显示单元。
对于三角形单元，长宽比是最长边除以该最长边上方三角形的高度。此比值乘以 (3/4) 的平方根，这样等边三角形的长宽比将为 1.0。
对于四边形单元（板和二维），将按照以下方式计算长宽比：最长边的长度除以最长边与四边形其他节点的最大距离。正方形的长宽比为 1.0。边为 1 和 2 的矩形长宽比为 2.0。
对于块体单元（8 节点），将连接三对相对面的中点以形成三条直线。这些线在块体的中心处交叉，每对线定义一个平面。对于由两条直线形成的每个平面，将计算从平面到第三条直线端点的距离除以形成平面的最长直线一半长度的比值。块体的长宽比是这三个比值中最大的。对于矩形实体，长宽比是任意面的最大四边形长宽比。
对于楔形体单元（6 节点块体），中间三角形由边直线的中点连接楔形体的三角形面构造。设 b 为中间三角形的最大边，h 为中间三角形的高度，hw 为端部三角形中点之间的直线长度。长宽比是 sqrt(3)*h/(2*b)、hw/b 和 b/hw 之中的最大值。通过将等边三角形拉伸一个边的距离创建的楔形体单元的长宽比为 1.0。
对于锥体单元（5 节点块体），设 h 为四边形中间面上方的点的高度。设 b 为四边形的最长中边直线，长宽比是四边形长宽比（h/b 和 b/h）的最大值。底为正方形且高度等于底边的锥体长宽比为 1.0。
对于四面体单元（4 节点块体），将为 4 个可能的底计算面积为 ai 的底部三角形上方的高度 hi。长宽比是所有 4 个底部三角形的 Cf * hi/sqrt(ai)、sqrt(ai)/(Cf * hi) 中的最大值。Cf 是 (3/4)^3/4，这样所有边相等的四面体的长宽比为 1.0。
- 长/短比：如果处于活动状态，将基于长/短比显示单元。长/短比是最长边的长度除以最短边的长度的比值。
- 面积与体积的比：如果处于活动状态，则将基于面积除以体积的比值显示实体单元。特别是，将通过（面积/6）的平方根除以体积的立方根定义“面积与体积的比”。立方体的面积与体积的比为 1.0。平面单元（板）的面积与体积的比为 1.0。
- 板厚度：此命令仅适用于板或壳单元。等值线将基于这些单元的厚度发生变化。
- 四面体坍塌比：此命令适用于包含 4 节点四面体单元的块体模型。选择后，将基于单元中的最长边长度与最短高度 (L/h) 的比值显示四面体单元。不会对其他单元类型进行着色。 提示： 由于需要显示完整的网格才能查看内部单元，且与其他单元类型相比，四面体单元数通常较少，因此很难与所有其他未着色单元一起查看其结果。使用“过滤模块”可仅选择已着色的单元，然后隐藏未选定的单元。
- 单元长度：如果激活，则将基于每个线单元（梁、桁架等）的长度显示单元。不会对其他单元类型进行着色。