Bruchmodell

Die Plastizitätsreaktion des Matrixkonstituentenmaterials wird insgesamt durch Eqs definiert. 1-8. Das Modell muss jedoch auch ein Bruchkriterium aufweisen, das den vollständigen Ausfall des mit kurzen Fasern gefüllten Materials identifiziert. Drei Bruchkriterien sind für die Verwendung mit Advanced Material Exchange verfügbar.

Polynombruch

Die Polynombruchmethode ist das Vorgabebruchmodell, das von Advanced Material Exchange verwendet wird. Bei der Polynombruchmethode gehen wir davon aus, dass das Matrixbruchkriterium als quadratische Funktion der Matrixdurchschnittsspannungs-Komponenten ausgedrückt wird.

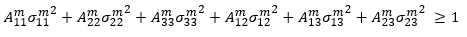
Die Größen 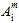(i = 11, 22, 33, 12, 13, 23) sind die anpassbaren Koeffizienten der Matrixausfallkriterien, die aus Zugtests für die Datensätze bei 0, 90 und 45 Grad festgelegt werden müssen. Falls Sie keine Spannungs-/Dehnungsdaten bei 45 Grad haben, verwenden wir die 90-Grad-Kurve und erhöhen die Spannungsdatenpunkte um 5 %. Weitere Informationen über die Bestimmung der Fehlerkoeffizienten finden Sie im Thema Materialcharakterisierung.

Der Satz der Fehlerkoeffizienten, die zum Berechnen von Brüchen verwendet werden, variiert je nach dem größten Eigenwert des Faserausrichtungstensors an jedem Integrationspunkt im Modell. Wenn der größte Eigenwert > 0.65 beträgt, setzen wir ein transversal isotropes Verhalten voraus, sodass σ₂₂^m = σ₃₃^m und σ₁₂^m = σ₁₃^m. Außerdem setzen wir die Scherspannungskomponente aus der Ebene σ₂₃^m = σ₁₂^m = σ₁₃^m voraus. Entsprechend gilt: A₂₂ = A₃₃ und A₁₂ = A₁₃ = A₂₃.

Wenn der größte Eigenwert ≤ 0.65 beträgt, setzen wir ein isotropes Verhalten voraus, sodass σ₁₁^m = σ₂₂^m = σ₃₃^m und σ₁₂^m = σ₁₃^m = σ₂₃^m. Entsprechend gilt: A₁₁ = A₂₂ = A₃₃ und A₁₂ = A₁₃ = A₂₃.

MCT

Bei der MCT-Methode gehen wir davon aus, dass das Matrixbruchkriterium als quadratische Funktion der Matrixdurchschnittsspannungskomponenten ausgedrückt wird.

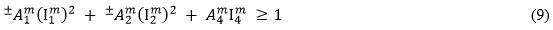
In Gleichung 9 sind die Größen 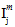(j = 1, 2, 4) transversale isotrope Invarianten des Matrixdurchschnittsspannungszustands.

Die Größen 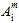(i = 1, 2, 4) sind die anpassbaren Koeffizienten der Matrixausfallkriterien, die aus Zugtests für die Datensätze bei 0, 90 und 45 Grad festgelegt werden müssen. Falls Sie keine Spannungs-/Dehnungsdaten bei 45 Grad haben, verwenden wir die 90-Grad-Kurve und erhöhen die Spannungsdatenpunkte um 5 %. Weitere Informationen über die Bestimmung der Fehlerkoeffizienten finden Sie im Thema Materialcharakterisierung.

Maximale effektive Spannung

Im Bruchmodell für die maximale effektive Spannung gehen wir davon aus, dass die Funktionsform des effektiven Spannungsausdrucks (eine Gewichtung von Mises-Spannungen, siehe Gleichung 6) ausreichend zur Definition der Richtungsabhängigkeit des Materials sowohl für die Prognose der Matrixplastizitätsentwicklung als auch für die Prognose des Matrixbruchs ist. Aus diesem Grund setzt die Bestimmung des Matrixbruchkriteriums voraus, dass eine Obergrenze für den Wert der gewichteten effektiven Spannung festgelegt wird (die effektive Festigkeit wird durch S_eff dargestellt). In diesem Fall wird die Matrixbruchbedingung wie folgt ausgedrückt

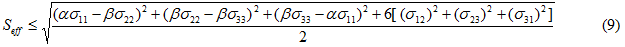
wo zu erkennen ist, dass die Spannungskomponenten die durchschnittliche Spannung im Matrixmaterial darstellen.

Schadensentwicklung

Wenn die Matrixbruchbedingung erfüllt ist (entweder MCT oder maximale effektive Spannung), werden einige Änderungen an den konstitutiven Beziehungen des ausgefallenen Materials vorgenommen.

1. Es ist nicht mehr notwendig, die Spannung und Dehnung des Verbundwerkstoffs in die Matrixspannung und -dehnung zu zerlegen, da die Kunststoffentwicklung für die Matrix nicht mehr länger berechnet werden muss.
2. Die konstitutiven Beziehungen des homogenisierten Verbundmaterials werden direkt verwendet und nicht mehr über die konstitutiven Beziehungen und die Mikrostruktur (wie bereits zuvor gezeigt) berechnet.
3. Die Steifheit des Verbundmaterials wird sofort auf einen Bruchteil der ursprünglichen elastischen Steifheit des Verbundmaterials reduziert. Die Steifigkeitsreduktion wird durch Multiplikation der Steifigkeitsmatrix mit einer Degradationskonstante ausgeführt. Beachten Sie, dass die Steifheit des Verbundmaterials nach dem Auslösen der Bruchbedingung für die Dauer der Simulation konstant bleibt und diesen reduzierten Wert hat.
4. Die konstitutiven Bedingungen des Verbundwerksoffs werden von einer Tangentenformulierung (die in der Plastizitätsphase der Materialreaktion verwendet wird) zu einer Sekantenformulierung geändert. Da die Steifheit des ausgefallenen Verbundwerksoffs konstant bleibt, hat der entsprechende Integrationspunkt keine direkte Auswirkung auf die Nichtlinearität der Lösung mehr.

Anmerkung: Die Schadensentwicklung beim Druck unterscheidet sich von der oben beschriebenen Methode. Weitere Informationen finden Sie im Thema Belastungsabfall bei Druck.