일-에너지 원리에 따르면, 두 접합 간의 압력 강하는 두 접합 사이의 모든 경로에서 동일해야 합니다. 일-에너지 방정식은 네트워크에서 압력을 계산하는 데 사용됩니다.
중요사항: 일-에너지 방정식은 네트워크 솔루션의 두 가지 원리를 충족하기 위해 각 절점의 연속 방정식 및 각 절점의 온도 방정식과 동시에 각 요소에서 해석됩니다.
일-에너지 원리 방정식은 두 접합 사이의 모든 경로에 대해 동일한 압력 손실을 충족해야 합니다.
압력 강하 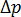 또는
또는 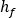 는 접합 절점에서 떨어져 나오는 요소의 분기에 대해 체적 유량 Q 함수로서 일반항으로 표현될 수 있습니다.
는 접합 절점에서 떨어져 나오는 요소의 분기에 대해 체적 유량 Q 함수로서 일반항으로 표현될 수 있습니다.
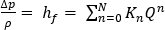
여기서 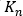 및
및 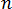 는 경험적으로 결정된 압력 강하와 유량의 관계에 종속된 변수이며, N은 압력 강하를 설명하는 데 사용되는 방정식의 차수를 나타냅니다.
는 경험적으로 결정된 압력 강하와 유량의 관계에 종속된 변수이며, N은 압력 강하를 설명하는 데 사용되는 방정식의 차수를 나타냅니다.
이 방정식은 네트워크에 압력이 추가되는 경우와 네트워크에서 압력이 손실되는 경우에 모두 유효합니다. 압력이 네트워크에 추가되는 경우(예: 펌프를 사용하는 경우) 압력은 음수 압력 손실로 간주됩니다.
주: 두 접합 사이의 압력 강하 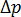 또는
또는 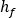 외에 다음 항목도 압력 손실에 기여하므로 압력 손실 계산에서 고려해야 합니다.
외에 다음 항목도 압력 손실에 기여하므로 압력 손실 계산에서 고려해야 합니다.
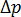 또는
또는 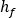 외에 다음 항목도 압력 손실에 기여하므로 압력 손실 계산에서 고려해야 합니다.
외에 다음 항목도 압력 손실에 기여하므로 압력 손실 계산에서 고려해야 합니다.
- 냉각관 벽의 유체 전단으로 인한 마찰 헤드 손실. 이러한 마찰 헤드 손실은 냉각관의 전체 길이에서 항상 존재하며, 냉각수 유동 해석에서 Darcy-Weisbach 방정식을 통해 해석됩니다.
- 밸브, 절곡부, T자형 접합 등 유체 스트림의 국부적 중단으로 인한 경미한 손실
- 압력을 추가하고 음의 헤드 손실로 간주되는 펌프
일-에너지 원리 방정식은 네트워크의 모든 요소에서 압력 강하 관계를 나타내야 합니다.
각 요소에 대한 일반적인 일-에너지 원리 방정식 해석
냉각수 유동 계산 도메인을 참조할 경우, 일반적으로 절점 i의 분기 요소 j에 대한 압력 강하 관계는 다음과 같이 표현될 수 있습니다.
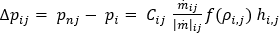
여기서 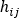 는 위의 일-에너지 원리에서 파생된 압력 강하 유량 관계이고,
는 위의 일-에너지 원리에서 파생된 압력 강하 유량 관계이고, 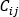 는 연결성 연산자 (+) 또는 (-)이며,
는 연결성 연산자 (+) 또는 (-)이며, 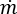 은 질량 유량이고,
은 질량 유량이고, 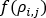 는 네트워크의 유체에 대한 밀도 함수입니다. 물과 같은 비압축성 유체의 경우 이는 상수입니다.
는 네트워크의 유체에 대한 밀도 함수입니다. 물과 같은 비압축성 유체의 경우 이는 상수입니다.
주: 일반적인 일-에너지 원리 방정식은 마찰 헤드 손실, 경미한 손실 및 펌프의 음의 헤드 손실을 고려하기 위해 Darcy-Weisbach 방정식을 통해 추가로 수정됩니다.
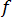 의 기능적 동작은 Moody 다이어그램에 자세히 표시되어 있으며, 이는 압축성 유체와 비압축성 유체 모두에 유효합니다.
의 기능적 동작은 Moody 다이어그램에 자세히 표시되어 있으며, 이는 압축성 유체와 비압축성 유체 모두에 유효합니다.