냉각 회로의 유동을 해석하려면 각 회로 요소의 정확한 유량과 함께 각 절점에서 정확한 압력을 계산해야 합니다.
냉각수 유동 해석은 두 가지 단순한 원리를 기반으로 합니다.
- 연속성 원리
- 네트워크의 모든 접합에 대해 접합으로 유입되는 총 유량이 접합에서 유출되는 총 유량과 동일하도록 하여 시스템 전체의 질량 보존을 충족해야 합니다. 또한 지름 변화에 상관없이 직렬로 연결된 파이프 또는 덕트에서 총 유량이 일정하게 유지되어야 합니다. 이 원리는 연속 방정식으로 표현되며, 후속 페이지에 설명되어 있습니다.
- 일-에너지 원리
- 두 접합 간의 압력 강하는 두 접합 사이의 모든 경로에서 동일해야 합니다. 이 원리는 일-에너지 방정식으로 표시되며, 헤드 손실, 경미한 손실 및 회로에 있는 모든 펌프의 기여도를 포함하도록 수정됩니다. 이러한 파생은 후속 페이지에 설명되어 있습니다.
회로 내 각 절점의 온도 및 압력과 각 요소의 유량을 해석하려면 이러한 방정식을 동시에 해석해야 합니다. 각각의 파생은 후속 페이지에 보다 자세히 설명되어 있습니다. 다음 방정식을 표현할 때 냉각수 유동 계산 도메인에 설명된 대로 인덱스 i는 네트워크의 절점을 나타내고, 인덱스 j는 절점에 연결된 요소의 분기를 나타낸다는 점에 유의해야 합니다.
유량에 대한 연속 방정식
각 절점에서 연속 방정식을 충족해야 합니다.
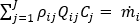여기서 i =1...절점 개수, j =1....분기 요소 개수
여기서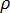 
는 유체 밀도, Q는 냉각관의 체적 유량, 
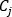는 고려할 절점의 지정된 분기에 대한 연결성 연산자 (+) 또는 (-)를 나타냅니다(냉각수 유동 계산 도메인의 설명 참조). 또한 질량 유향 
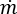은 모든 내부 절점에 대해 0이고, 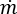은 지정된 경계면 절점에 대해 네트워크를 출입하는 질량 플럭스입니다.
압력 강하에 대한 일-에너지 방정식
유량 압력 강하 관계는 일반적인 일-에너지 원리 방정식에 설명된 대로 각 절점에 연결된 각 분기 요소에서 충족되어야 합니다.
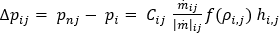
여기서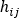 
는 일-에너지 원리 방정식에서 파생된 압력 강하 유량 관계이고, 
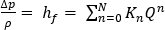는 연결성 연산자 (+) 또는 (-)이며, 
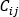은 질량 유량이고,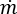 
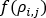는 네트워크의 유체에 대한 밀도 함수입니다. 물과 같은 비압축성 유체의 경우 이는 상수입니다.
- 마찰 헤드 손실과 경미한 손실 포함
-
그러나, 금형 냉각 회로에는 헤드 손실과 경미한 손실이 모두 적용되므로 더 구체적인 버전의 유량 압력 강하 관계가 사용됩니다. 유체 전단으로 인한 헤드 손실은 모든 직선 파이프의 유체 유동에 의한 것입니다. Darcy-Weisbach 방정식은 파이프 또는 덕트의 직선 길이에서 마찰로 인한 압력 강하를 계산합니다. 경미한 손실은 피팅, 밸브, 절곡부, 엘보우, T자형, 입구, 출구, 확대 및 수축을 통과하는 유동으로 인한 압력 손실입니다. 다음과 같이 마찰 헤드 손실과 경미한 손실을 포함하도록 일반적인 일-에너지 원리 방정식을 수정할 수 있습니다.
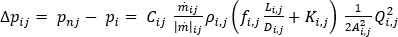
여기서
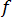는 마찰 계수, D는 냉각관의 지름, L은 냉각관의 길이, K는 저항 계수(제조업체에서 얻을 수 있음), A는 냉각관의 단면적, Q는 냉각관의 체적 유량을 나타냅니다.
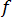도 레이놀즈 수에 무관합니다.
- 펌프 포함
-
분기에 펌프 또는 팬 요소가 연결된 경우 적용되는 관계는 다음과 같습니다.
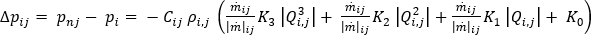
계산에 중력이 포함하는 경우 경계면 절점에서 고도가 고려됩니다. 이 옵션은 기본적으로 선택되어 있지 않습니다.
온도 방정식
각 절점의 온도는 해당 절점에 유입되는 유체의 총 에너지에서 얻을 수 있으며, 다음 방정식으로 지정됩니다.
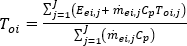
여기서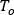 
는 유체 온도이고, 방정식의 오른쪽은 분기 요소를 나타냅니다. 또한 
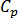는 유체의 비열, 
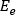는 요소 e에 전달되는 에너지, 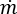은 요소의 질량 유량입니다.