Transient response analysis is the most general method for computing forced dynamic response. The purpose of a transient response analysis is to determine the behavior of a structure subjected to time-varying excitation. The transient excitation is explicitly defined in the time domain. The loads applied to the structure are known at each instant in time. Loads can be in the form of applied forces and enforced motions. The results obtained from a transient response analysis are typically displacements, velocities, and accelerations of grid points, and forces and stresses in elements, at each output time step.
Depending upon the structure and the nature of the loading, two different numerical methods can be used for a transient response analysis:
- Direct Transient Response Analysis, which calculates the response of a system to a load over time. The load applied to the system can vary over time or simply be an initial condition that is allowed to evolve over time. This method may be more efficient for models where high-frequency excitation require the extraction of a large number of modes. Also, if structural damping is used, the direct method should be used.
- Modal Transient Response Analysis, which is an alternate technique available for dynamics that utilizes the mode shapes of the structure, reduces the solution degrees of freedom, and can significantly impact the run time. This approach replaces the physical degrees of freedom with a reduced number of modal degrees of freedom. Fewer degrees of freedom mean a faster solution. This can be a big time saver for transient models with a large number of time steps. Because modal transient response analysis uses the mode shapes of a structure, this analysis is a natural extension of normal modes analysis.
Direct Transient Response Theory
In direct transient response analysis, the structural response is computed by solving a set of coupled equations using direct numerical integration. The method used is the same as for nonlinear transient response and allows for an adaptive time stepping algorithm. We begin with the dynamic equation of motion in matrix form:
The fundamental structural response (displacement) is solved at discrete times, typically at a series of time steps with a constant time increment between them. The solution strategy is called the central finite difference method and is based on finding the displacement, velocity and acceleration at subsequent times, knowing those values at the current and past times. The image below shows a transient integration graph.
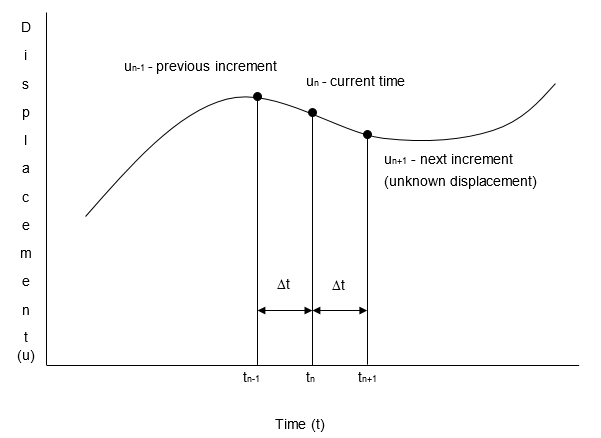
At any time n, we know the displacement, velocity and acceleration. Using this information, there are a number of ways to find the displacement, velocity and acceleration at a subsequent step. For example, if we assume the current velocity remains constant until the next time increment, the subsequent displacement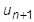 
would simply be the current location plus the velocity times the time increment,
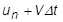. However, if the velocity is not constant, something we cannot assume in a general problem, we have to account for a changing velocity, so that we have an acceleration term in the equation.
This is true if we assume the current acceleration remains constant to the next increment. However, this cannot necessarily be assumed in a general problem. The mean value theorem postulate an acceleration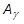 
is a function of a constant gamma such that the acceleration is a weighted average of the accelerations at n and n+1:
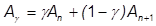
Newmark was able to show that 0.5 is a good value for gamma, such that:
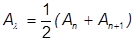
and
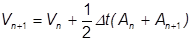
Since velocity is the first derivative of displacement, and acceleration the second, they are usually represented in dot notation as their derivatives.
However, since the acceleration may vary with time as well, we can propose that the displacement will be corrected by both velocity and acceleration terms thus:
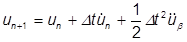
The acceleration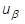 
in the above term is calculated like the velocity above, such that:
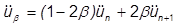
u can then be written in terms of the beta constant:
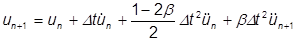
The beta value in the above equation is called the Newmark-Beta, and can vary between 0 and 1. It is usually used as ¼, which yields the constant average acceleration method, where:
These equations can be manipulated to find expressions for velocity and acceleration at the current time increment, but expressed in terms of the displacement at past and subsequent time intervals:
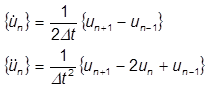
These representations are then substituted into the equations of motion, resulting in the following:
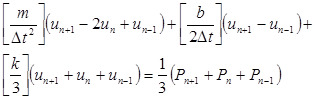
However, since 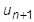is the unknown, we need a 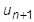value in each expression for the solution. We will represent the displacement at the current time as the average over the adjacent times. Likewise the load can be averaged over three steps, the difference being that we know 
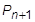as it is an input value.
Using these average values:
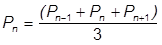
We then rearrange the terms to end up with the unknown 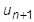on the left side and the known 
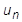and 
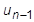on the right:
To solve this equation, we need to calculate the four A terms, then decompose (invert) the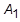 
term to find 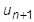. It should be noted that for a problem with a constant time step that 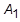need be decomposed only once. However, if the time step changes, it will be necessary to do the calculation again. Thus, it is advisable to maintain a constant time step unless changing it will offset the extra cost.
Modal Transient Response Theory
To run a modal transient response analysis, it is necessary to transform the physical coordinates to modal coordinates. The natural frequencies and eigenvectors are a good way to do this because of their property of orthogonality. As such, we can replace the physical coordinates u with the modal coordinates:
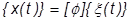
The basic equation of motion (temporarily ignoring the damping term) becomes:
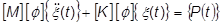
With a little manipulation, we can rearrange this into something more useful:
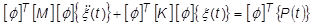
But the mass and stiffness terms are now the generalized modal matrices, diagonal matrices that are easily handled:
= modal or generalized mass matrix
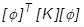= modal or generalized stiffness matrix
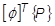= modal load vector
The diagonal matrices have the effect of uncoupling the modal degrees of freedom. The load term is a vector and is already uncoupled. As a result, the system is easily solved as a series of uncoupled equations:
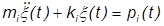
Where m and k are the generalized mass and stiffness values for each modal degree of freedom, and p is the modal load vector.
Once values are found for the modal displacements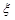 
, the physical displacements can be found from the sum of the modal displacements:
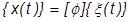
This approach will yield the exact same answer as the direct approach, provided that all modal degrees of freedom (DOF) are included in the transformation. However, the strength of the approach comes about because an answer that is very close to exact can usually be obtained with significantly fewer modal degrees of freedom than there are physical degrees of freedom. With fewer DOF, the solution can proceed much faster. This can be especially efficient for large models and for models that require many time steps.
|
Previous Topic: Frequency Response Analysis Exercise |
Next Topic: Damping in Dynamic Analysis |