The frequency response analysis is used to compute structural response to steady-state oscillatory excitation. In frequency response analysis, the excitation is explicitly defined in the frequency domain. Excitations can be in the form of applied forces and enforced motions (displacements, velocities, or accelerations).
There are two types of frequency response analysis:
- Direct Frequency Response Analysis, where the structural response is computed at discrete excitation frequencies by solving a set of coupled matrix equations using complex algebra. The direct method may be more efficient for models where high-frequency excitation require the extraction of a large number of modes.
- Modal Frequency Response Analysis, which is an alternate method to compute frequency response. This method uses the mode shapes of the structure to uncouple the equations of motion (when no damping or only modal damping is used) and, depending on the number of modes computed and retained, reduce the problem size. Both of these factors tend to make modal frequency response analysis computationally more efficient than direct frequency response analysis. It is used for large models where a large number of solution frequencies are specified. This method replaces the physical degrees of freedom (DOF) with a reduced number of modal degrees of freedom. Fewer degrees of freedom mean a faster solution. Because modal frequency response analysis uses the mode shapes of a structure, modal frequency response analysis is a natural extension of normal modes analysis.
Direct Frequency Response Theory
A direct frequency response starts with the general equations of motion, but assumes an oscillating load:
We can then propose that the solution is also in the form of an oscillating function:
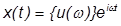
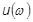is a complex displacement vector. The velocity and acceleration can be found by taking the derivative:
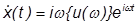
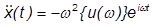
Substitute this into the equation of motion and divide by the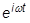 
term to get:
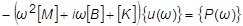
The frequency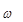 
is a constant in this equation. Therefore, the solution will yield a complex displacement vector u for each frequency that is selected.
In a direct frequency response analysis, this equation is solved repeatedly for each selected frequency. As a result, the solution time is proportional to the number of frequencies that are selected for solution.
Modal Frequency Response Theory
To run a modal frequency response, it is necessary to transform the physical coordinates to modal coordinates. The natural frequencies and eigenvectors are a good way to do this because of their property of orthogonality. As such, we can replace the physical coordinates u with the modal coordinates. So first, a transformation is defined:
This is substituted into the equations of motion (temporarily ignoring the damping term):
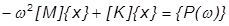
Resulting in the following:
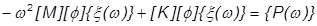
Now pre-multiply by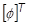 
:
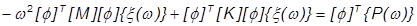
These terms are replaced with the uncoupled generalized components that are easily handled:
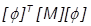= modal or generalized mass matrix
= modal or generalized stiffness matrix
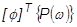= modal load vector
Resulting in an uncoupled series of equations that are easily solved:
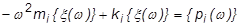
And once the modal displacements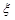 
are found, the physical displacements can be found from the sum of the modal displacements:
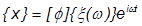
This approach will yield the exact same answer as the direct approach, provided that all modal degrees of freedom are included in the transformation. However, the strength of the approach comes about because an answer that is very close to exact can usually be obtained with significantly fewer modal degrees of freedom than there are physical degrees of freedom. With fewer DOF, the solution can proceed much faster. This can be especially efficient for large models and for models with large numbers of frequencies.
|
Previous Topic: Modal Avoidance Exercise |
Next Topic: Frequency Response Analysis Exercise |