断裂模型
基体成分材料的塑性响应由以下方程共同定义1-8。但是，模型还必须利用标识短纤维填充材料是否完全失效的断裂准则。有三种断裂准则可与 Advanced Material Exchange 结合使用。
多项式应力
多项式应力方法是 Advanced Material Exchange 所用的默认断裂模型。在多项式应力方法中，我们假设基体断裂准则是基体平均应力分量的二次函数。
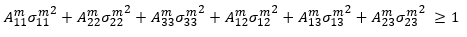
量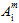 
(i = 11, 22, 33, 12, 13, 23) 是基体失效准则的可调整系数，它们必须通过 0、90 和 45 度数据集的拉伸测试进行确定。如果您没有 45 度的应力-应变数据，我们将使用 90 度曲线，并将应力数据点提升 5%。请参考材料特征化主题，了解有关如何确定失效系数的更多详细信息。
评估断裂时所使用的失效系数集会有所不同，具体取决于模型中每个积分点处纤维取向张量的最大特征值。当最大特征值大于 0.65 时，我们假定横向各向同性行为，即 σ22m = σ33m 且 σ12m = σ13m。我们还假定平面外剪切应力分量 σ23m = σ12m = σ13m。相应地，A22 = A33 且 A12 = A13 = A23。
当最大特征值小于等于 0.65 时，我们假定各向同性行为，即 σ11m = σ22m = σ33m 且 σ12m = σ13m = σ23m。相应地，A11 = A22 = A33 且 A12 = A13 = A23。
MCT
在 MCT 方法中，我们假设以基体平均应力分量的二次函数形式来表示基体断裂准则。
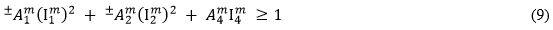
在方程9 中，量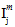 
(j = 1, 2, 4) 是基体平均应力状态的横向各向同性不变量。
量 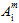(i = 1, 2, 4) 是基体失效准则的可调整系数，它们必须通过 0、90 和 45 度数据集的拉伸测试进行确定。如果您没有 45 度的应力-应变数据，我们将使用 90 度曲线，并将应力数据点提升 5%。请参考材料特征化主题，了解有关如何确定失效系数的更多详细信息。
最大有效应力
在“最大有效应力”断裂模型中，我们假设函数形式的有效应力表达式（加权 von Mises 应力，请参见方程6）足以为基体塑料演变的预测和基体断裂的预测定义材料的定向依赖关系。因此，基体断裂准则的确定要求我们仅设定加权有效应力测量值（表示有效强度 Seff）的上限。在这种情况下，基体断裂准则表示为
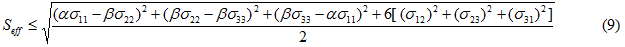
不用说，应力分量表示基体成分材料中的平均应力。
损坏演变
当满足基体断裂条件时（MCT 或最大有效应力），将对失效材料的本构关系进行一些更改。
- 由于我们不必再计算基体的塑料演变，因此不再需要将复合材料应力和应变分解为基体应力和应变。
- 可以直接使用均质化的复合材料的本构关系，而不是从成分本构关系和微观结构生成复合本构关系（如前文所述）。
- 复合材料的刚度会瞬时缩减到复合材料原始弹性刚度的很小一部分。此刚度缩减由刚度基体乘以降级常数执行。请注意，触发断裂条件后，复合材料的刚度在模拟的持续时间内将固定在缩减后的值。
- 复合本构关系将从切线公式（已在材料响应的塑性阶段使用）切换为割线公式。由于失效复合材料的刚度保持不变，因此有疑问的积分点不再对求解的非线性产生任何直接的影响。