Para definir los parámetros de análisis modal para los nuevos casos dinámicos de la estructura, realice una de las siguientes acciones:
- Seleccione un caso de análisis modal en el cuadro de diálogo Nuevo caso y seleccione Aceptar.
- Seleccione un caso de análisis modal en el cuadro de diálogo Tipo de análisis y haga clic en Definir parámetros.
Es recomendable aplicar un solvente iterativo para solucionar problemas a gran escala, ya que proporciona tres métodos para resolver problemas de valores propios. Para ello, seleccione Solvente iterativo en el cuadro de diálogo Análisis estructural de Preferencias para el proyecto.
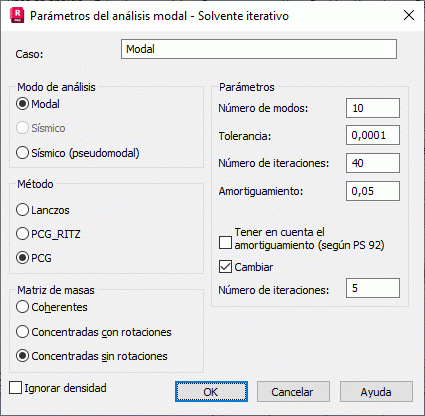
Modo de análisis
Actualmente, para el solvente iterativo, están disponibles los modos Modal y Sísmico (pseudomodo). Solo se puede acceder al modo Modal para el gradiente conjugado preacondicionado (PCG) [1-4]. El modo Sísmico (pseudomodo) está disponible para los métodos de Lanczos modificado y gradiente Ritz (PCG_Ritz).
Método
Método de Lanczos
Lanczos es un método de Lanczos modificado que evita la factorización de una matriz a gran escala. El método de gradiente conjugado preacondicionado (PCG) genera una colección de vectores de Lanczos en lugar de realizar la resolución posterior de la matriz de rigidez de cálculo. Están disponibles todos los tipos de preacondicionamiento definidos para el análisis estático (Herramientas > Preferencias para el proyecto > Iterativo > Parámetros).
El método de Lanczos modificado es preferible en análisis sísmicos y espectrales de grandes estructuras cuando se necesitan muchos modos.
- Parámetros requeridos
Tipo de la matriz de masas (concentrada con rotaciones o coherente) y número de modos.
La precisión del cálculo depende de la tolerancia prevista de cálculo de los vectores de Lanczos y el número de modos. La tolerancia se asigna en Herramientas > Preferencias para el proyecto > Iterativa > Parámetros y es la misma que para los casos estáticos. La opción Tolerancia del cuadro de diálogo Parámetros de análisis modal - Solvente iterativo indica una tolerancia para una solución de un problema de valores propios generalizado, incluidos los vectores de Lanczos definidos, y no puede ser menor que 1.0e-04.
Cuanto mayor sea el número de modos contabilizados, más próximos estarán los vectores de Ritz bajos a los valores propios adecuados. La suma de las masas modales será más exacta.
PCG_Ritz
PCG_Ritz es un método de Ritz en el que el enfoque de gradiente preacondicionado se utiliza para generar una colección de vectores base (método de gradiente Ritz [5]). El método PCG_Ritz es preferible para las definiciones rápidas aproximadas de pares propios durante los análisis sísmicos y espectrales. Es necesario seleccionar un método multinivel. También es recomendable asignar un nivel de agregación. Este método resultará eficaz para problemas de tamaño mediano (hasta 60.000 ecuaciones). Están disponibles todos los tipos de preacondicionamiento definidos para el análisis estático (Herramientas > Preferencias para el proyecto > Iterativo > Parámetros).
- Parámetros requeridos
Tipo de la matriz de masas (concentrada con rotaciones o coherente) y número de modos. La precisión de los cálculos depende del número de modos.
PCG
PCG es un método de gradiente conjugado preacondicionado [1-5]; su uso es preferible cuando se define un número reducido de modos propios. Por ejemplo, el método PCG puede resultar muy útil al aplicar cargas de viento o comprobar un número reducido de modos bajos obtenidos mediante el método PCG_Ritz. Están disponibles todos los tipos de preacondicionamiento definidos para el análisis estático (Herramientas > Preferencias para el proyecto > Iterativo > Parámetros). Se pueden aplicar todos los tipos de matriz de masas (coherentes, concentradas con rotaciones y concentradas sin rotaciones).
- Parámetros requeridos:
Número de modos; Tolerancia: criterios de precisión en relación con la detección de iteraciones; Número de iteraciones: número máximo permitido de iteraciones para cada modo (el proceso de iteración se detiene en cada modo si el parámetro de tolerancia actual es inferior al valor de Tolerancia o si el número de iteraciones actual supera el valor de Número de iteraciones); Cambiar: aprovecha la técnica de desplazamiento para la aceleración por convergencia; Número de repeticiones: determina un número de repeticiones (para cada modo, el algoritmo realiza las iteraciones determinadas por Número de iteraciones, corrige un valor de desplazamiento y repite las iteraciones determinadas por Número de iteraciones el número de veces definido en Número de repeticiones).
- Parámetros recomendados:
Método multinivel o no multinivel con enfoque ICCF (Herramientas > Preferencias para el proyecto > Iterativo > Parámetros); nModos £ 5; Tolerancia = 0.01; Número de iteraciones = 100 para un método no multinivel; Cambiar: desactivado.
- Tipo de matriz de masas.
- Parámetros (número de modos, tolerancia, número de iteraciones y amortiguamiento).
- Cambiar (con número de iteraciones).
Impedir la configuración incorrecta del solvente iterativo
Un sistema de control impide que los parámetros de análisis modal sean incorrectos para los solventes iterativos. Se activa cuando se hace clic en Aceptar para iniciar el análisis modal. Se muestra una solicitud de parámetros de análisis. Haga clic en Sí para aceptar los valores de los parámetros determinados en el cuadro de diálogo. Haga clic en No para volver al cuadro de diálogo Parámetros del análisis modal y realizar correcciones.
Si se utiliza un solvente iterativo en los cálculos en el modo Sísmico (pseudomodo), realice lo siguiente:
- El número de niveles de agregación debe ser igual a 1 (Preferencias para el proyecto > Análisis de la estructura/Parámetros > Iterativo).
- El número de modos buscado que se especifique debe ser al menos tres veces mayor de lo necesario.
- Se debe comprobar la convergencia de la solución en busca del número de modos presentado en el punto 2 y un número de modos dos veces mayor. Si no hay convergencia (valores propios claramente diferentes para el número de modos dos veces superior al número inicial), debe aumentarse el número de modos. Una vez obtenida la solución convergente, se puede aplicar el filtrado de modos para limitar el número de modos.
Para un tipo de análisis de este tipo, el parámetro Tolerancia de los resultados del análisis dinámico no tiene ningún significado práctico y se puede ignorar. Si no se siguen estas recomendaciones, el error podría alcanzar varias decenas de porcentaje.
Referencias
- Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrices, J. Comp. Phys., 74: 41 - 60, 1988.
- Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Phys., 81: 53 - 69, 1989.
- Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Meth. Appl. Mech. Eng., 62: 195 - 207, 1987.
- M.Papadrakakis, Solving large -scale problems in mechanics, John Wiley & Sons Ltd., 1993.
- Fialko S., High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis, CAMES, 7: 537 - 550, 2000.
Consulte también:
Parámetros del análisis modal que reconoce esfuerzos estáticos
Descripción del análisis modal que reconoce esfuerzos estáticos
Descripción del método de iteración en el subespacio por bloques
Análisis modal: precisión de los cálculos