El análisis modal determina los valores propios y derivados (pulsaciones propias, frecuencias propias o periodos propios), la precisión, los vectores propios, los coeficientes de participación y las masas participantes para el problema de las vibraciones propias de la estructura.
Hay disponibles tres modos de análisis dinámico de la estructura (modal, sísmico y sísmico [pseudomodal]).
Los valores propios y los modos propios se obtienen a partir de la siguiente fórmula.
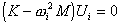(1)
donde:
K: matriz de rigidez de la estructura,
M: matriz de masas de la estructura,
ωi: pulsación natural (frecuencia circular natural) del modo "i",
Ui: vector de modo propio del modo "i".
El número de modos propios que se deben tener en cuenta se puede especificar como se indica a continuación:
- El límite superior de la pulsación, la frecuencia o el periodo.
- El límite inferior de la suma de masas participantes (porcentajes) o como el número real de modos requeridos.
Si no se especifica el número de modo, se utiliza en el análisis el valor definido por defecto en Preferencias.
Los parámetros de control del algoritmo de problema con valores propios son los siguientes:
- Precisión de los cálculos (cantidad de errores).
- Número máximo de iteraciones.
Están disponibles los siguientes tipos de matriz de masas:
- Coherentes (matriz coherente, siempre con respecto a los grados de libertad de rotación),
- Concentradas con rotaciones (matriz diagonal, con respecto a los grados de libertad de rotación),
- Concentradas sin rotaciones (matriz diagonal sin grados de libertad de rotación).
Las matrices de masas concentradas (Mlum) se crean de acuerdo con la regla:
Mlum(i,j) = 0.0 ; para i≠j
Mlum(i,j) = Stot/Sdiag * M(i,j) ; para i=j (2)
donde:
Stot: suma de todos los elementos de la matriz coherente de masas M,
Sdiag: suma de los elementos diagonales de la matriz coherente de masas M.
Por lo tanto, la masa del elemento se conserva y la matriz de masa del elemento se define como positiva.
Los vectores propios de los módulos de resultados se normalizan de forma que el término máximo de cada vector sea 1.0.
Los vectores propios internos utilizados durante los cálculos se normalizan de modo que:
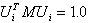(3)
El valor de precisión que se muestra en el cuadro de diálogo Valor propio se considera la precisión de convergencia obtenida. Este valor representa la cantidad aceptable de errores en cuanto a la precisión con la que el valor propio λi y el vector propio Ui obtenidos durante la iteración del modo i-th se ajustan a la ecuación del problema con valores propios:
K * Ui = λi * M * Ui (4)
Los coeficientes de participación se definen del siguiente modo:
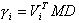
donde:
D: vector unitario definido como se indica a continuación:
D(j) = 1.0 si j es igual al grado de libertad de i-th
D(j) = 0.0 si j es ¹ i,
Vi: vector propio del modo i normalizado de modo que: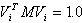 
Las masas participantes son dinámicas y participan en el movimiento de la estructura con cada modo y cada grado de libertad. Se consideran las masas actuales del modo actual y las masas relativas resultantes de la suma de las masas actuales desde el primer modo hasta el actual. Los valores se presentan como un porcentaje de las masas dinámicas totales.
Las masas participantes actuales se definen de la siguiente manera:
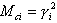
Actualmente, el algoritmo de Lanczos, que constituye un enfoque muy útil para resolver problemas con valores propios a gran escala (1), es el método predeterminado para encontrar la solución a estos problemas. Encuentra n valores propios y vectores propios necesarios con cualquier nivel de precisión.
En la mayoría de los casos, el método de Lanczos es el más adecuado. No obstante, se aplican las restricciones siguientes:
- La matriz tridiagonal T no debe ser de tipo coherente.
- La matriz de masas M debe tratarse como concentrada con rotaciones o como coherente. Si se selecciona Concentradas sin rotaciones, la matriz de masas se añade automáticamente como Concentradas con rotaciones.
Cuando se selecciona un método de Lanczos en un programa, este cambia el método de cálculo a un método de iteración en el subespacio. Para utilizar el método de Lanczos en los cálculos, las estructuras disyuntas deben estar conectadas de forma que no se modifique el modelo de la estructura (por ejemplo, se debe añadir una barra entre los apoyos).
La siguiente reducción de la matriz tridiagonal T se aplica en el método de Lanczos:
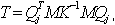
donde
Qj = {q1, q2, ..., qj}: matriz rectangular Neq x j, Neq: número de ecuaciones, j: número de pasos de Lanczos, qj: vector de Lanczos j-th.
La fórmula
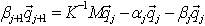
se utiliza para generar el siguiente vector de Lanczos qj+1 y define la línea actual de la matriz T.
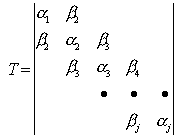
Por lo tanto, el problema con valores propios reducido es el siguiente:
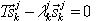, k=1,2,…,j
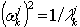, donde ωk j es la aproximación de j-th a ωk, k=1,2,…,n y n es el número necesario de valores propios y vectores propios. Un algoritmo realizará los cálculos (aumentando el número j de pasos de Lanczos) hasta que se alcance la precisión necesaria para n valores propios.
El procedimiento de ortogonalización admite el nivel de ortogonalidad requerido entre los vectores de Lanczos, lo que garantiza la seguridad y la estabilidad numérica de los cálculos.
Los vectores propios se obtienen a partir de las siguientes fórmulas:
U = Qs.
Método de reducción de la base
El método de reducción de la base obtiene valores aproximados de los primeros valores propios, siempre que ya se hayan recopilado algunos datos sobre ellos. Este método requiere la asignación de grados de libertad principales (MDOF) para obtener el sistema reducido. Una vez realizada esta acción, se puede crear el modelo reducido y se pueden excluir de este los grados de libertad no deseados, lo que dará como resultado un sistema con un tamaño mucho menor. Resulta especialmente útil para quienes tienen experiencia en el análisis dinámico de la estructura y cuando se conoce el comportamiento de la estructura dinámica.
Las siguientes reglas se aplican a este método:
- Se deben especificar los grados de libertad principales (nudos principales y direcciones). Se presupone que solo los desplazamientos (y no las rotaciones) se pueden asignar como grados de libertad principales.
- Se puede utilizar cualquier tipo de matriz de masas en el algoritmo. Sin embargo, el tipo de matriz Concentradas sin rotaciones garantiza el período de cálculo más corto.
- Verificación de Sturm indica el número de frecuencias omitidas. No se encontrarán estos valores y vectores propios. La única forma de encontrar la convergencia de verificación es aumentar el número de grados de libertad principales para resolver el problema y comparar los valores propios.
El método incluye la transformación del problema con valores propios de gran volumen en el modelo FEM.
K U - ω2 M U = 0 al problema con valores propios en un modelo reducido:
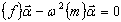
donde {f}: matriz de influencia, {m}: matriz generalizada para el modelo reducido.
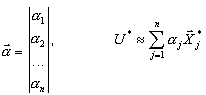
Las soluciones obtenidas para los estados de unidad adecuados son la base de dichas transformaciones:
Se aplican fuerzas nodales unitarias en consecuencia para cada nudo de tipo principal en la dirección seleccionada del tipo principal. El problema estático a gran escala se ha resuelto en n lados derechos:
K Xi * = Ti , i = 1, 2, …, n
donde Ti: vector de carga correspondiente a la fuerza de la unidad i-th. Se deben definir nudos y direcciones de tipo principal; el resto de operaciones se ejecutarán automáticamente. A continuación, el problema con valores propios reducido se resuelve con el método de Jacobi. Como resultado, se obtienen los valores aproximados de las frecuencias wi y los vectores propios Ui * , i=1,2,...n.
Consulte también:
Análisis modal: precisión de los cálculos en el análisis modal estructural