Cada nudo tiene su propio sistema local; por lo tanto, no se requiere el sistema de coordenadas local de un elemento finito completo. Es importante conocer la orientación del vector normal con respecto a la superficie del elemento finito. Preferiblemente, los vectores normales de todos los elementos finitos deben tener la misma orientación. De lo contrario, la definición de carga de un elemento (como la presión perpendicular a la superficie de la lámina) puede ser incorrecta.
La orientación de un vector normal (perpendicular a la superficie de un elemento de lámina) se determina según la regla de la mano derecha (en la dirección del primer al último nudo del elemento). En la siguiente figura, que representa elementos finitos de 6 y 8 nudos, se muestran los sistemas de coordenadas locales y la orientación del vector normal con respecto a la superficie del elemento.
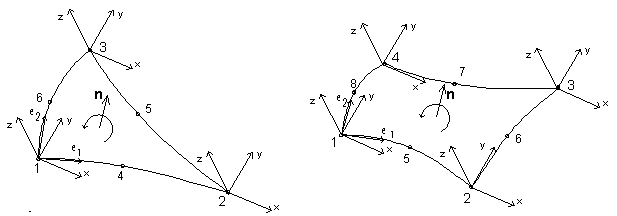
Para los elementos finitos planos, se obtienen las fuerzas y tensiones en un elemento. Se determinan en función de la ubicación con respecto al vector normal local y a la tangente de la sección transversal. Se adoptan las siguientes convenciones de signos:
- n: el vector normal a la superficie de la sección transversal del elemento
- s: el vector tangencial a la superficie de la sección transversal del elemento
- z: la normal externa a la superficie del elemento
Estos vectores forman un sistema de coordenadas cartesianas acorde a la regla de la mano derecha. La orientación positiva de las fuerzas, los momentos y las tensiones en una sección transversal determinada se define según la orientación de los vectores n/s/z. Esto se muestra de forma esquemática en la siguiente figura. Las fuerzas, los momentos y las tensiones que se muestran en la figura tienen signos positivos.
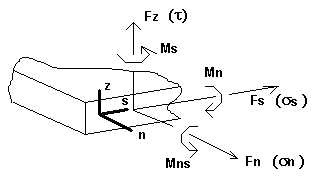
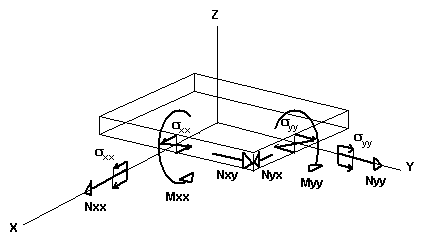
Los resultados obtenidos para los EF planos se presentan en sistemas de coordenadas locales que el usuario puede definir y modificar en cualquier momento durante la presentación de los resultados. Por ejemplo, la orientación positiva de las fuerzas y las tensiones correspondientes en un nudo se presentan con el eje X como dirección de referencia.
Consulte también el siguiente tema: