Les structures de câble sont des structures dans lesquelles les câbles sont les principaux éléments porteurs. Un câble est un élément ayant plusieurs propriétés : 1) l'une de ses dimensions principales est beaucoup plus grande que les autres; 2) sa rigidité transversale au fléchissement et à la torsion est peu importante par rapport à la rigidité longitudinale à la traction.
La conséquence simple de la définition donnée est qu’un câble transfère seulement les efforts de traction. Parfois il peut aussi transférer des moments de flexion ou de torsion peu importants et des efforts tranchants. Le principal avantage de l'utilisation de structures à câbles est le fait que les câbles admettent des contraintes de traction significatives.
Par conséquent, il est possible d'envisager une section de câble pour concevoir des structures légères, économiques et esthétiques. Deux facteurs sont décisifs en ce qui concerne l’utilisation des câbles dans les structures :
- Entrez la première tension de câble afin de réguler l'effort interne et d'optimiser les résultats.
- Assemblage simple (par exemple, suspension et assemblage d'une structure entière, en raison de sa légèreté).
Dans la théorie des structures de câble on adopte les principes de base suivants :
- Les charges et autres effets externes sont de type quasi-statique et ne varient pas au fil du temps.
- Pour les câbles, aucun moment de flexion ni effort tranchant n'est pris en compte.
- Les éléments de câbles fonctionnent dans le domaine élastique (module de Young E = const).
- N'importe quelle charge peut être appliquée, à l’exception des charges par moments.
- Des déplacements importants u, mais de faibles gradients du/dx, sont tolérés.
- L'aire de la section du câble F est invariable (F=const).
- Longueur du câble non chargé = l
Equations régissant le problème
Prenons en considération un câble extensible à flèche peu importante (câble présentant un angle réduit la tangente à un point quelconque du câble et la droite reliant ses deux extrémités), et appliquons-lui une charge quelconque dans son plan. Supposons un élément infinitésimal dans ce câble, décrit à l'étape initiale (première phase d'assemblage) par la charge q0, la température T0 et la tension H0 ; la longueur de cet élément est égal à dso (Fig. 1a). Après l’application de la charge (deuxième, finale étape du câble) pour le chargement q, température T et tension H, la longueur du segment élémentaire du câble est égale à ds (fig.1b). Les deux étapes avec les charges dans les deux plans (xy et xz) sont représentées en Fig. 2.
 Fig. 1a |
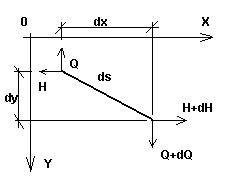 Fig. 1b |
La flèche du câble étant peu importante, et l’effort total dans le câble devant être dirigé le long de la tangente au câble, on peut déterminer l’allongement élémentaire correspondant du segment du câble uniquement en fonction des valeurs statiques. Après l’intégration de cette valeur sur toute la longueur du câble, nous obtenons la forme connue de l’équation du câble extensible à flèche peu importante. De (1), on obtient la valeur D, correspondant à l’allongement de la corde du câble.
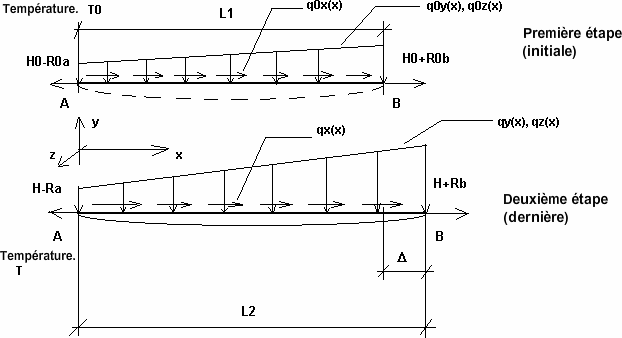
Fig. 2
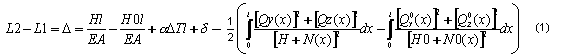
où :
A, B - nœud de câble d'origine et d'extrémité
EF - rigidité de la tension du câble (où : E - module de Young, F - surface de section transversale du câble)
a - coefficient de dilatation thermique
l - longueur initiale du câble (pour le câble non chargé)
D - changement de la distance entre les appuis
d - raccourcissement/allongement interne initial du câble (réglage)
DT - changement de température
Q(x) - fonction du changement de l’effort tranchant similaire à une poutre appuyée librement (en fonction des indices respectivement dans la direction de l’axe y et z et pour l’étape initiale ou finale) - Voir Fig. 3a.
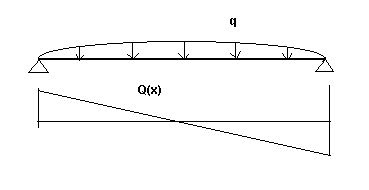
Fig. 3a
N(x) - fonction du changement de l’effort axial provoqué par une charge tangente pour une poutre encastrée des deux côtés (pour l’étape initiale et finale) - Voir Fig. 3b.
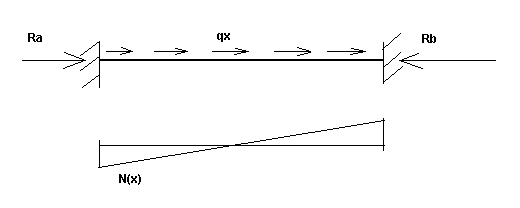
Figure 3b
On observe aussi dans l'équation du câble (1), à la différence des solutions classiques appliquées lors du calcul des câbles, que la force longitudinale peut varier le long du câble (dans les dénominateurs des deux fonctions d'intégration de l’équation (1) apparaissent les composants fonctionnels : [H+N(x)] 2 et [H0+N0(x)] 2 ). Cette équation permet aussi d'obtenir des résultats plus précis.
Rubrique connexe :