La théorie de l’élément câble utilisée dans le logiciel Robot est basée sur la théorie générale du câble extensible avec une flèche peu importante. Selon cette théorie, la rigidité du câble est une fonction implicite des paramètres suivants : rigidité de la tension du câble (E * F), tension du câble, déplacements de l'appui du câble et charge transversale dans les deux directions (p y p z ).
Il faut attirer l’attention sur le fait que la définition des éléments câbles dans une structure, à cause du caractère non linéaire de leur travail, exige l’utilisation des méthodes itératives de l’analyse des structures.
Possibilités de mise en œuvre des câbles dans le logiciel Robot :
- Les éléments câbles peuvent être utilisés conjointement avec des éléments des types de structure suivants : PORTIQUE 2D, PORTIQUE 3D, et COQUE.
- Tous les types d'analyse de structure standard sont admis : linéaire (en fait, c’est une analyse non linéaire mais les effets non linéaires, excepté la non-linéarité des éléments câbles eux-mêmes, ne seront pas pris en compte), non linéaire (pour l’effet contrainte-raidissement), P-Delta, incrémentiel, flambement, dynamique, harmonique, sismique; Remarque : L'analyse dynamique est traitée comme linéaire par rapport à la rigidité en cours.
- Les excentrements sont admis
- Le matériau est défini comme pour une barre (il faut donner seulement le module de Young E en cas de définition du poids mort du câble comme charge : de plus, il faut définir le poids unitaire RO et, en cas de définition des charges thermiques, le coefficient de dilatation thermique LX),
- Les angles GAMMA sont définis comme pour les barres (important uniquement pour la description de la charge).
Limitations :
- Pour les éléments câbles, la définition des relâchements est impossible parce qu’ils n’ont pas de rigidité à la flexion ni à la torsion.
Charges des éléments câbles
Les charges suivantes s'appliquent aux éléments câbles :
- Charges nodales
- Charges permanentes
- Charges linéaires (uniformes ou variables d’une façon linéaire)
- Raccourcissement/allongement initial (charges supplémentaires appliquées lors de la phase de montage)
- Charge thermique
- Charges par forces concentrées sur la longueur des éléments.
Les charges suivantes ne s'appliquent pas aux éléments câbles :
- Moment
- Moment réparti
SYNTAXE (données saisies par l’utilisateur dans un fichier texte)
PROpriétés
(<liste des éléments>) CABles AX=<aire de section> (E=<module de Young>)
(RO=<poids unitaire>) [PREContrainte= <s> | TENSion = <h> | LONgueur= <l>
| [ DILatation = <d> (RELative) ]]
où :
PREContrainte - contrainte normale (calculée par rapport à la corde du câble) qui doit être atteinte pour les charges du cas de montage
TENSion - force de tension (calculée par rapport à la corde du câble) qui doit être atteinte pour les charges du cas de montage
LONgueur - longueur du câble non chargé
DILatation - différence entre la longueur du câble non chargé et la distance entre les nœuds sur lesquels le câble est ancré (si la valeur est positive, la longueur du câble est supérieure à la distance entre les nœuds, si la valeur est négative, la longueur du câble est inférieure à la distance entre les nœuds)
DILatation RELative - proportion de la différence entre la longueur du câble non chargé et la distance des nœuds sur lesquels le câble est ancré (si la valeur est positive, la longueur du câble est supérieure à la distance entre les nœuds, si la valeur est négative, la longueur du câble est inférieure à la distance entre les nœuds).
- Le module de Young E peut être défini dans la définition du matériau
- Mots-clés : les contraintes, la force, la longueur et la dilatation sont explicitement définies et ne sont pas requises. Si aucun de ces paramètres n'est spécifié, la longueur du câble est égale à la distance entre les nœuds.
Chargement du câble - Cas de montage
Le logiciel Robot inclut la phase de montage de la structure. Il est recommandé qu'elle soit le premier cas de charge. La syntaxe de ce cas de charge est la suivante :
CAS
ASSemblage
[description des charges]
Pour ce cas de charge :
- Dans les barres indiquées agissent les forces de tension initiale dont la valeur est définie par l’utilisateur à la suite de la détermination d’une des valeurs ci-dessous dans la syntaxe du fichier texte (commande PROpriétés) :
PREContrainte = s0 (contrainte initiale du câble) ou
TENSion = t0 (effort de tension initial dans le câble)
- On peut définir la longueur initiale du câble non tendu et non chargé en déterminant LONgueur= l
0
, si elle doit être différente de la valeur par défaut LONG =
 , égale à la distance entre les nœuds,
, égale à la distance entre les nœuds, - On peut définir le raccourcissement/allongement initial du câble à l’aide de la commande DILatation (RELative)
- Si le mot clé RELative n’apparaît pas, la DILatation est donnée en valeurs absolues
- S'il existe un mot-clé RELative, l'allongement initial est exprimé sous la forme d'une fraction, la dernière longueur du câble est égal à : L = LONG (1 + DIL).
- Toutes les charges définies sont appliqués (par exemple, charge permanente et masses ajoutées).
- On peut définir la température TX pour les câbles dans la phase de montage
- Les déplacements calculés pour ce cas de charge définissent la géométrie initiale pour les autres cas de l’analyse de la structure.
Lors de l’analyse des cas suivants, les charges sur la structure dans les conditions d’équilibre, les charges appliquées dans le cas de montage sont prises en compte. Les déplacements définis pour ce cas sont considérés comme initiaux. Les efforts de tension qui ont été prédéfinis changent (cela signifie que les câbles ont été ancrés après le montage).
Forme de l’équation du câble extensible pour l’étape de montage
À cette étape, l’équation (1) décrit le passage :
- du câble non chargé (câble au sol) :
q0x = q0y = q0z = 0 (pas de charge)
H0 = 0 (pas de tension du câble)
T0 = 0
Dans cette équation, la longueur est égale à L1= :
1.
long, quand (long ≠ 0) - si la valeur LONgueur est donnée dans la définition du câble
2.
[distance(A, B) + dilatation], quand la dilatation est définie dans le repère absolu - si la valeur DILatation est donnée dans la définition du câble
3.
[distance(A, B)*(1+dilatation], quand la dilatation est définie dans le repère relatif - si la valeur DILatation RELative est donnée dans la définition du câble
4.
[distance(A, B)], quand (dilatation = 0) et (long = 0) - si aucun des mots-clés LONgueur, DILatation et DILatation RELative n’apparaît dans la définition du câble ou qu'apparaît un des mots-clés suivants :
à
- câble monté dans la structure avec toutes les charges du premier cas de charge (cas de montage), à savoir :
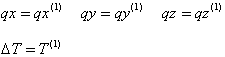
L2 est la distance entre les nœuds de fixation A et B du câble déformé :
L2 = distance (A + U un , B + U B )
où :
U A - Déplacement du point A
U B - Déplacement du point B.
Différents cas spécifiques du premier cas de charge (cas de montage) sont possibles :
- L’effort H est connu (contrôlé) - cela arrive quand PREContrainte ou effort de TENSion sont différentes de zéro (PREContrainte¹ 0 ou TENSion ¹ 0). L’effort de tension est alors égal à :
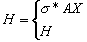
De l’équation (1), on obtient :

La valeur L est prise comme la distance entre les nœuds origine et extrémité du câble.
A partir de l'équation (2), on peut affecter le premier allongement D du câble, essentiel pour obtenir la force requise H :

- L’effort de tension H est inconnu (dans la définition de la syntaxe du câble n’est donnée ni la valeur de la PREContrainte, ni celle de la TENSion), alors :
- Si les déplacements lors de la phase de montage sont pris en considération, (définis par les valeurs de LONgueur, DILatation ou DILatation RELative dans la syntaxe du câble), c’est-à-dire :

alors, on solutionne l’équation (4) en fonction de l’effort H

et on procède à l’itération du système d’équations entier, par conséquent on obtient la valeur finale de l’effort de montage.
Elle est égale à :
 .
. - Si nous ne prenons pas en compte les déplacements des nœuds, c’est-à-dire :
L2 = distance (A, B)
en solutionnant l’équation (4), nous obtiendrons la valeur initiale de l’effort nécessaire pour suspendre le câble entre les appuis.
- Si les déplacements lors de la phase de montage sont pris en considération, (définis par les valeurs de LONgueur, DILatation ou DILatation RELative dans la syntaxe du câble), c’est-à-dire :
- L’effort H est connu (contrôlé) - cela arrive quand PREContrainte ou effort de TENSion sont différentes de zéro (PREContrainte¹ 0 ou TENSion ¹ 0). L’effort de tension est alors égal à :
Cas de charge du câble après le montage
Après l’achèvement des calculs de la structure, les résultats obtenus pour les éléments câbles sont similaires aux résultats pour les éléments barres ; toutefois, quelques différences subsistent Les différences incluent :
- Aucun effort tranchant ni aucun moment ne peuvent être obtenus pour les éléments câbles
- Pour les éléments câbles, on obtient une déformation simplifiée (définie comme pour une barre de treillis) ou une déformation exacte (définie d’après l’équation différentielle de la courbe de la flèche),
- Résultats supplémentaires pour les éléments câbles (conséquence de l'étape d'assemblage) :
- Dans les câbles pour lesquels une tension est nécessaire (dans la syntaxe Robot : PREcontrainte ou TENSion), la valeur de la réglementation [m] requise pour la tension est affectée
- Dans d'autres câbles, la force de tension essentielle au montage est affectée
Ces résultats sont utiles pour la conception de la phase de montage. Ils sont disponibles dans le module Résultats en sélectionnant la commande : Contraintes > Paramètres > Résultats pour les éléments câbles dans la phase de montage.
- La force axiale (de traction) est définie d’après l’équation :

où :
N - effort agissant le long de la tangente au câble,
FX, FY, FZ - composants de l’effort N projetés en direction des axes spécifiques du repère local du câble.
Equation du câble lors du travail du câble dans la structure
Lorsqu'un cas arbitraire (I) est défini après le premier cas de montage, le comportement du câble est obtenu par la résolution de l'équation (1). L'itération d'une telle équation est exécutée selon les hypothèses suivantes :

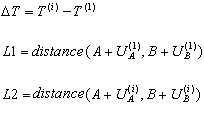
![]() La charge du le premier cas de charge est automatiquement ajoutée à la charge dans le cas (i)
La charge du le premier cas de charge est automatiquement ajoutée à la charge dans le cas (i)
La force de tension H est inconnue.
Rubrique connexe :