Die transiente Antwortanalyse ist die allgemeinste Methode für die Berechnung der erzwungenen dynamischen Antwort. Ziel einer transienten Antwortanalyse ist die Bestimmung des Verhaltens einer Struktur bei zeitabhängiger Erregung. Die transiente Erregung wird im Zeitbereich explizit definiert. Die auf die Konstruktion wirkenden Lasten sind zu jedem Zeitpunkt bekannt. Lasten können in Form von angewendeten Kräften und erzwungenen Bewegungen auftreten. Bei den Ergebnissen aus einer transienten Antwortanalyse handelt es sich in der Regel um Verschiebungen, Geschwindigkeiten und Beschleunigungen von Rasterpunkten sowie Kräfte und Spannungen an Elementen für jeden einzelnen ausgegebenen Zeitschritt.
Je nach Art der Konstruktion und der Belastung kann man für eine transiente Antwortanalyse zwei verschiedene numerische Methoden nutzen:
- Die direkte transiente Antwortanalyse berechnet die Antwort eines Systems auf eine Last im Zeitverlauf. Die in einem System auftretende Last kann sich im Lauf der Zeit ändern. Es kann sich auch einfach um eine Anfangsbedingung handeln, die sich im Lauf der Zeit weiterentwickeln kann. Für Modelle, bei denen aufgrund der hochfrequenten Erregung sehr viele Modi extrahiert werden müssen, ist diese Methode möglicherweise effizienter. Bei struktureller Dämpfung sollte ebenfalls die direkte Methode verwendet werden.
- Die modale transiente Antwortanalyse ist ein alternatives Verfahren für Dynamik, wobei die Modusformen der Konstruktion verwendet und die Lösungs-Freiheitsgrade reduziert werden. Dies kann erhebliche Auswirkungen auf die Laufzeit haben. Bei dieser Methode werden die physischen Freiheitsgrade durch eine geringere Anzahl modaler Freiheitsgrade ersetzt. Weniger Freiheitsgrade bedeuten eine schnellere Lösung. Bei transienten Modellen mit vielen Zeitschritten kann man hierdurch viel Zeit sparen. Da die modale transiente Antwortanalyse die Modusformen der Konstruktion verwendet, ist sie eine natürliche Erweiterung der normalen Modusanalyse.
Theorie der direkten transienten Antwort
Bei der direkten transienten Antwortanalyse erfolgt die Berechnung der Strukturreaktion durch das Lösen von gekoppelten Gleichungen mittels direkter numerischer Integration. Die verwendete Methode ist die gleiche wie für nichtlineare transiente Antwort und ermöglicht einen adaptiven Algorithmus mit Zeitstaffelung. Wir beginnen mit der dynamischen Bewegungsgleichung in Matrixform:
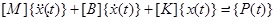
Die grundlegende strukturelle Reaktion (Verschiebung) wird für einzelne Zeitpunkte berechnet, in der Regel für eine Reihe von Zeitschritten mit konstanten Zeitinkrementen. Die Lösungsstrategie nennt sich zentrale Finite-Differenzen-Methode und basiert auf der Ermittlung der Verschiebung, Geschwindigkeit und Beschleunigung zu aufeinanderfolgenden Zeitpunkten und der Kenntnis dieser Werte zum jetzigen Zeitpunkt und in der Vergangenheit. Die folgende Abbildung zeigt ein Diagramm der transienten Integration.
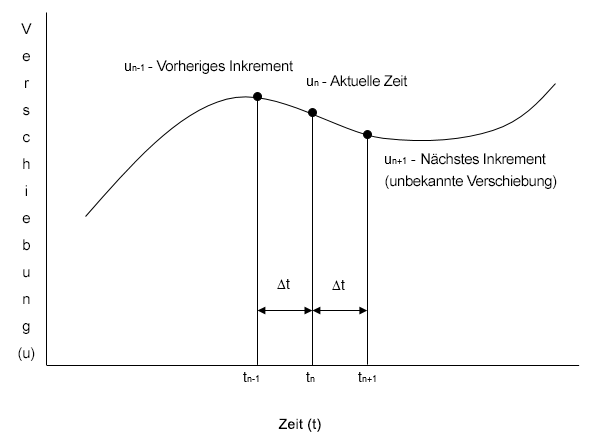
Wir kennen die Verschiebung, Geschwindigkeit und Beschleunigung zu jedem Zeitpunkt n. Mit diesen Informationen gibt es verschiedene Möglichkeiten, die Verschiebung, Geschwindigkeit und Beschleunigung bei einem nachfolgenden Schritt zu ermitteln. Nehmen wir beispielsweise an, dass die aktuelle Geschwindigkeit bis zum nächsten Zeitschritt konstant bleibt. Dann wäre die nachfolgende Verschiebung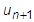 
einfach die aktuelle Position plus die Geschwindigkeit multipliziert mit dem Zeitinkrement 
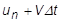. Allerdings können wir bei einer allgemeinen Aufgabenstellung nicht von einer konstanten Geschwindigkeit ausgehen. Wir müssen die Geschwindigkeitsänderung berücksichtigen und nehmen daher einen Term für die Beschleunigung in die Gleichung auf.
Dies gilt unter der Annahme, dass die aktuelle Beschleunigung bis zum nächsten Inkrement konstant bleibt. Davon kann jedoch bei einer allgemeinen Aufgabenstellung nicht notwendigerweise ausgegangen werden. Der Mittelwertsatz besagt, dass die Beschleunigung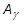 
eine Funktion einer Konstante Gamma ist, sodass die Beschleunigung der gewichtete Mittelwert der Beschleunigungen bei n und n+1 ist:
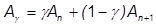
Newmark konnte zeigen, dass 0,5 ein geeigneter Wert für Gamma ist, sodass:
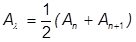
und
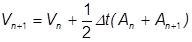
Da die Geschwindigkeit die erste und Beschleunigung die zweite Ableitung der Verschiebung ist, werden diese normalerweise durch Überpunkte als Ableitungen dargestellt.
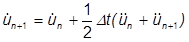
Da jedoch die Beschleunigung im Zeitverlauf ebenfalls variieren kann, dürfen wir nicht davon ausgehen, dass die Verschiebung durch die Terme für Geschwindigkeit und Beschleunigung korrigiert wird. Daher:
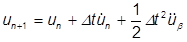
Die Beschleunigung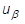 
im obigen Term wird genauso berechnet wie die Geschwindigkeit darüber, sodass:
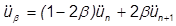
u kann dann mit der Beta-Konstante beschrieben werden:
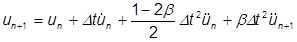
Der Beta-Wert in der obigen Gleichung wird Newmark-Beta genannt und kann wechselnde Werte zwischen 0 und 1 annehmen. In der Regel wird er mit ¼ verwendet. Daraus ergibt sich die Methode des konstanten Mittelwerts, wobei:
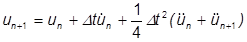
Diese Gleichungen können abgewandelt werden, um Ausdrücke für die Geschwindigkeit und die Beschleunigung für das aktuelle Zeitinkrement zu erhalten, jedoch ausgedrückt als Verschiebung bei den vorhergehenden und nachfolgenden Zeitintervallen:
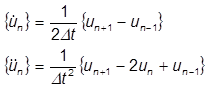
Diese Darstellungen werden dann in die Bewegungsgleichungen eingesetzt, was zu folgendem Ergebnis führt:
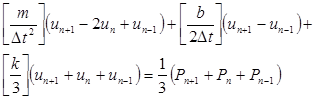
Da jedoch 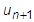die Unbekannte ist, brauchen wir für die Lösung in jedem Ausdruck einen Wert 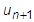. Wir stellen die Verschiebung zum aktuellen Zeitpunkt als Durchschnitt über die benachbarten Zeiten dar. Ebenso kann die Last über drei Schritte gemittelt werden. Der Unterschied besteht darin, dass wir 
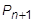kennen, da es sich um einen Eingabewert handelt.
Wir verwenden diese Durchschnittswerte:
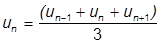
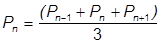
Dann formen wir die Gleichung so um, dass die Unbekannte 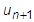auf der linken Seite und die Bekannten 
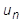und 
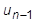auf der rechten Seite stehen:
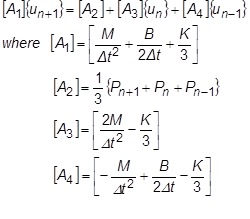
Zur Lösung dieser Gleichung berechnen wir die vier A-Werte und lösen den Term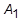 
durch Umkehren auf, um 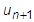zu erhalten. Beachten Sie, dass bei einer Aufgabenstellung mit konstantem Zeitschritt 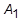nur einmal aufgelöst werden muss. Wenn sich jedoch der Zeitschritt ändert, muss die Berechnung erneut durchgeführt werden. Daher ist es empfehlenswert, einen konstanten Zeitschritt beizubehalten, sofern die Zusatzkosten nicht durch die Änderung wieder hereingeholt werden.
Theorie der modalen transienten Antwortanalyse
Zur Durchführung einer modalen transienten Antwortanalyse müssen die physischen Koordinaten in modale Koordinaten umgewandelt werden. Aufgrund ihrer Orthogonalität sind die Eigenfrequenzen und Eigenvektoren hierfür gut geeignet. Deshalb können wir die physischen Koordinaten u durch modale Koordinaten ersetzen:
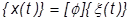
Die grundlegende Bewegungsgleichung (bei vorübergehender Vernachlässigung des Dämpfungsterms) wird zu:
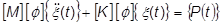
Nach einer kleinen Bearbeitung können wir dies in eine nützlichere Form bringen:
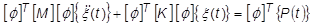
Die Terme für Steifigkeit und Masse sind nun aber generalisierte modale Matrizen, diagonale Matrizen, die leicht zu verarbeiten sind:
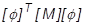= modale oder generalisierte Massenmatrix
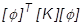= modale oder generalisierte Steifigkeitsmatrix
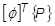= modaler Lastvektor
Die diagonalen Matrizen haben zur Folge, dass die modalen Freiheitsgrade entkoppelt werden. Der Last-Term ist ein Vektor, der bereits entkoppelt ist. Hierdurch lässt sich das System leicht in eine Reihe von entkoppelten Gleichungen auflösen:
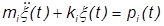
Dabei sind m und k die generalisierten Werte für Masse und Steifigkeit für jeden modalen Freiheitsgrad und p ist der modale Lastvektor.
Sobald Werte für die modalen Verschiebungen 
ermittelt sind, können die physischen Verschiebungen aus der Summe der modalen Verschiebungen ermittelt werden:
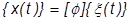
Auf diese Weise erhalten wir genau das gleiche Ergebnis wie bei direktem Vorgehen, vorausgesetzt, dass alle modalen Freiheitsgrade (FHG) in der Umformung enthalten sind. Die Stärke dieses Ansatzes besteht jedoch darin, dass ein sehr nahe am genauen Wert liegendes Ergebnis meist mit einer deutlich geringeren Anzahl an modalen Freiheitsgraden erzielt werden kann als die Anzahl der physischen Freiheitsgrade. Mit weniger Freiheitsgraden kann die Lösung viel schneller erfolgen. Dies kann besonders bei großen Modellen und Modellen mit vielen Zeitschritten effizient sein.
|
Vorheriges Thema: Frequenzantwortanalyse – Übung |
Nächstes Thema: Dämpfung bei dynamischen Analysen |