Jede reale Struktur gibt Energie ab (hauptsächlich durch Reibung). Deshlab ist Dämpfung eine wichtiger Teil der Realität. Normalerweise würde die Dämpfung bei nicht transienten Ereignissen (wie z B.Windlast oder Mengenlast) ignoriert, wäre aber für transiente Ereignisse (z. B. Erdbebenlast oder Bombenexplosion) wichtig.
Verschiedene Arten von Dämpfung bilden bei dynamischen Lösungen die Dämpfungsmatrix [B]. Die Dämpfungsmatrix besteht also mehreren Matritzen:

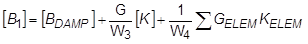
Dabei gilt:
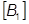 = Dämpfung aus Dämpfungselementen (CVISC, CDAMPi) und B2GG DMIG
= Dämpfung aus Dämpfungselementen (CVISC, CDAMPi) und B2GG DMIG
 = Dämpfung aus B2PP DMIG
= Dämpfung aus B2PP DMIG
 = globale Steifigkeitsmatrix
= globale Steifigkeitsmatrix
 = globale Massenmatrix
= globale Massenmatrix
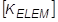 = Elementsteifheitsmatrix
= Elementsteifheitsmatrix
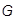 = Gesamt-Strukturdämpfungskoeffizient (PARAM, G)
= Gesamt-Strukturdämpfungskoeffizient (PARAM, G)
 = Element-Strukturdämpfungskoeffizient (GE bei MATi-Eintrag)
= Element-Strukturdämpfungskoeffizient (GE bei MATi-Eintrag)
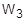 = gewünschte Frequenz in Radianten pro Zeiteinheit (PARAM, W3) für die Konvertierung der Strukturdämpfung insgesamt in die entsprechende viskose Dämpfung
= gewünschte Frequenz in Radianten pro Zeiteinheit (PARAM, W3) für die Konvertierung der Strukturdämpfung insgesamt in die entsprechende viskose Dämpfung
 = gewünschte Frequenz in Radianten pro Zeiteinheit (PARAM, W4) für die Konvertierung der Strukturdämpfung des Elements in die entsprechende viskose Dämpfung
= gewünschte Frequenz in Radianten pro Zeiteinheit (PARAM, W4) für die Konvertierung der Strukturdämpfung des Elements in die entsprechende viskose Dämpfung
 = Skalierfaktor der Steifigkeitsmatrix mit Rayleigh-Dämpfung
= Skalierfaktor der Steifigkeitsmatrix mit Rayleigh-Dämpfung
 = Skalierfaktor der Massenmatrix mit Rayleigh-Dämpfung
= Skalierfaktor der Massenmatrix mit Rayleigh-Dämpfung
Die folgende Tabelle zeigt, wie einige der verschiedenen Dämpfungsbegriffe sich auf die verschiedenen Lösungen auswirken.
| Direkte Frequenzantwort | Modale Frequenzantwort | Direkte transiente Antwort | Modale transiente Antwort | |
| Dämpfungselemente | Normal | Kraftgekoppelte Lösung | Normal | Kraftgekoppelte Lösung |
| Strukturdämpfung | Normal | Normal | Umgewandelt in äquivalent-viskos | Umgewandelt in äquivalent-viskos – Kraftschlüssige Lösung |
| Modale Dämpfung | Ignoriert | Normal | Ignoriert | Normal |
| Raleigh-Dämpfung | Kraftgekoppelte Lösung | Kraftgekoppelte Lösung | Normal | Normal |
Soifern möglich, liegt es in Ihrem eigenen Interesse, eine Dämpfung zu verwenden, den Einträgen unter Normal in der obigen Tabelle entspricht. Diese Kombinationen ergeben die schnellsten Laufzeiten.
Dämpfung bei direkter Frequenzantwort
Bei einer Aufgabenstellung mit direkter Frequenzantwort verwenden Sie eine komplexe Lösung. Dies hat zur Folge, dass der komplexen Dämpfungsterm unverändert übernommen werden kann. Es ist nicht nötig, die Strukturdämpfung in die entsprechende viskose Dämpfung umzuwandeln. Alle Formen der Dämpfung können schadlos verwendet werden.
Dämpfung bei modaler Frequenzantwort
Bei der modalen Lösung diagonalisiert die Dämpfungsmatrix in der Regel nicht. Darüber hinaus erzeugen alle strukturellen Dämpfungen eine komplexe Steifigkeitsmatrix, die ebenfalls nicht diagonalisiert. Wenn eine dieser Dämpfungsarten enthalten ist, muss die Lösung also in der direkten Methode, aber mit modalen Koordinaten erfolgen. Dies ist schneller als die Lösung im physischen Bereich, jedoch nicht so schnell wie die Lösung nicht gekoppelter Gleichungen. Um die Vorteile der nicht gekoppelten Lösung auszuschöpfen, muss auf andere Dämpfungsarten verzichtet und ausschließlich modale Dämpfung eingesetzt werden, wodurch die einzelnen modalen Freiheitsgrade individuell geändert werden.
Dämpfung bei direkter transienter Antwort
Die transiente Antwort lässt die Verwendung komplexe Koeffizienten nicht zu. Daher ist die Strukturdämpfung durch die äquivalente viskose Dämpfung enthalten.
Die viskose Dämpfungskraft ist eine Dämpfungskraft, die auf Basis eines Dämpfungskoeffizienten b und der Geschwindigkeit funktioniert. Es ist eine induzierte Kraft, die in der Bewegungsgleichung mit der Matrix [B].und dem Geschwindigkeitsvektor dargestellt wird.

Dabei gilt:
 = globale Massenmatrix
= globale Massenmatrix
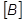 = globale Dämpfungsmatrix
= globale Dämpfungsmatrix
 = globale Steifigkeitsmatrix
= globale Steifigkeitsmatrix
 = globaler Lastvektor
= globaler Lastvektor
 = globaler Beschleunigungsvektor
= globaler Beschleunigungsvektor
 = globaler Geschwindigkeitsvektor
= globaler Geschwindigkeitsvektor
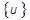 = globaler Verschiebungsvektor
= globaler Verschiebungsvektor
Die strukturelle Dämpfungskraft ist eine verschiebungsabhängige Dämpfung. Die strukturelle Dämpfungskraft ist eine Funktion eines Dämpfungskoeffizienten 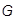 und einer komplexen Komponente der strukturellen Steifigkeitsmatrix.
und einer komplexen Komponente der strukturellen Steifigkeitsmatrix.
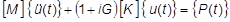
Unter der Annahme einer oszillierenden Antwort bei konstanter Amplitude für eine einzelnes Freiheitsgradsystem sind die beiden Dämpfungskräfte identisch, wenn:

Oder:

Wenn also die Strukturdämpfung 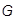 unter Verwendung der äquivalenten viskosen Dämpfungb modelliert werden soll, dann besteht diese äquivalenz nur bei einer Frequenz (siehe Abbildung unten).
unter Verwendung der äquivalenten viskosen Dämpfungb modelliert werden soll, dann besteht diese äquivalenz nur bei einer Frequenz (siehe Abbildung unten).

Diese beiden Parameter werden verwendet, um die strukturelle Dämpfung in die entsprechende viskose Dämpfung umzuwandeln. Ein Gesamtkoeffizient für die strukturelle Dämpfung kann mit PARAM, W3, r auf die gesamte System-Steifigkeitsmatrix angewendet werden, wobei r die Kreisfrequenz ist, bei der die Dämpfung gleich wird. Dieser Parameter wird zusammen mit PARAM, G verwendet. Der Vorgabewert für W3 ist Null, wodurch die Dämpfung aus dieser Quelle bei transienten Analysen ignoriert wird.
PARAM, W4 ist ein alternativer Parameter, der für die Umwandlung von Element-Strukturdämpfung in äquivalente viskose Dämpfung verwendet wird. PARAM, W4, r wird verwendet, wenn r die Kreisfrequenz ist, bei der die Dämpfung äquivalent werden soll. PARAM, W4 wird gemeinsam mit dme Felds GE beime MATi-Eintrag verwendet. Das Ergebnis für W4 ist Null, wodurch die Dämpfung aus dieser Quelle bei der transienten Analysen ignoriert wird.
Die Einheiten für PARAM, W3 and PARAM, W4 sind in Radianten pro Zeiteinheit. Die Wahl zwischen W3 und W4 ist üblicherweise die dominante Frequenz, bei der Dämpfung aktiv ist. Es kommt häufig vor, dass die erste Eigenfrequenz ausgewählt wird, aber eine isolierte Elementdämpfung kann bei verschiedenen Frequenzen auftreten und durch die entsprechenden Dateneingaben verarbeitet werden.
Dämpfung bei modaler transienter Antwort
Die modale transiente Antwortanalyse verwendet die Modusformen der Struktur, um die Größe zu verringern, Bewegungsgleichungen zu entkoppeln und die Effizienz der numerischen Integration zu steigern.
Um den Vorgang zu erläutern, werfen wir zunächst einen Blick auf die allgemeine Gleichgewichtsgleichung für ein bewegtes Finite-Elemente-System:

Die Umwandlung von physischen Koordinaten 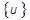 in modale Koordinaten
in modale Koordinaten  lautet wie folgt:
lautet wie folgt:

Die Modusformen  dienen zum Umformen der Gleichung nach dem Modusverhalten im Gegensatz zum Verhalten der Rasterpunkte.
dienen zum Umformen der Gleichung nach dem Modusverhalten im Gegensatz zum Verhalten der Rasterpunkte.
Wenn wir davon ausgehen, dass die modale Dämpfung verwendet wird, können wir die allgemeine Gleichgewichtsgleichung folgendermaßen umschreiben:

Dies ist nun die Bewegungsgleichung nach modalen Koordinaten. Um die Gleichungen zu entkoppeln, multiplizieren Sie sie zuerst mit  und erhalten dann:
und erhalten dann:
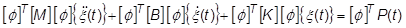
Dabei gilt:
 = modale oder generalisierte Massenmatrix
= modale oder generalisierte Massenmatrix
 = modale oder generalisierte Steifigkeitsmatrix
= modale oder generalisierte Steifigkeitsmatrix
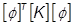 = modale Dämpfungsmatrix
= modale Dämpfungsmatrix
 = modaler Kraftvektor
= modaler Kraftvektor
Durch die Orthogonalität der Modusformen können wir die Bewegungsgleichungen mit der diagonalen verallgemeinerten Masse, Steifheit und Dämpfung (modale Dämpfung) formulieren. Da diese Matrizen keine nichtdiagonalen Terme beinhalten, welche die die Bewegungsgleichungen verknüpfne, sind die modalen Bewegungsgleichungen entkoppelt. Die Bewegungsgleichungen können dann folgendermaßen geschrieben werden:

Dabei gilt:
 = i-te modale Masse
= i-te modale Masse
 = i-te modale Dämpfung
= i-te modale Dämpfung
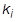 = i-te modale Steifigkeit
= i-te modale Steifigkeit
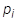 = i-te modale Kraft
= i-te modale Kraft
 = i-ter modaler Freiheitsgrad
= i-ter modaler Freiheitsgrad
Die obige Gleichung kann auch folgendermaßen geschrieben werden:

Dabei gilt:
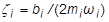 = modales Dämpfungsverhältnis
= modales Dämpfungsverhältnis
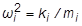 = modale Frequenz
= modale Frequenz
Die physischen Reaktionen werden dann folgendermaßen aus der Summe der einzelnen modalen Antworten ermittelt:
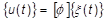
|
Vorheriges Thema: Transiente Antwortanalyse |