Eine Modal- oder Eigenfrequenzanalyse (auch bekannt als Normalmodi oder Eigenwertanalyse) bildet die Grundlage für mehrere dynamische Analysen, darunter Formulierungen für modale Ansätze und Antwortspektrumanalyse. Außerdem erfahren Sie aus den Ergebnissen einer Modalanalyse viel über die dynamischen Eigenschaften des Modells, beispielsweise, ob überhaupt ein dynamisches System vorliegt. Daher wird meist zuerst eine Normalmodusanalyse durchgeführt, um die grundlegende Dynamik des Modells zu untersuchenund nach Modellierungsproblemen zu suchen.
Die Ergebnisse dieser Analysen erzeugen eine Modusform und Frequenz. Beachten Sie, dass die ausgegebene Modusform ein Eigenvektor mit einem auf 1,0 gesetzten Maximalwert ist. Daher werden die resultierenden Verformungen so skaliert, dass die größte Verformung innerhalb der Struktur 1,0 beträgt und nicht repräsentativ für das Maß der Verformung, das bei tatsächlichen Schwingungen zu erwarten ist.
Eine Modalanalyse kann Abhängigkeiten beinhalten oder auch nicht. Bei Modellen, die ohne Abhängigkeiten ausgeführrt werden, sollten die ersten sechs Frequenzen im Prinzip 0 sein, da es sich um einen "freien" Modus handelt. Modelle mit teilweiser mit Abhängigkeit haben weniger als 6 "freie" Modi.
Eigenwert-Theorie
Stellen Sie sich ein dynamisches System vor. Im allgemeinen können die Bewegungsgleichungen als Funktion der Systemmasse, Steiffigkeit, Dämpfung und anliegenden Lasten ausgedrückt werden:
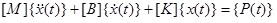
Dabei gilt:
[M] = globale Massenmatrix
[K] = globale Steifigkeitsmatrix
[B] = globale Dämpfungsmatrix
{P} = globaler Lastvektor
Eigenwerte oder Eigenfrequenzen sind dort zu finden, wo es keine Dämpfung oder anliegende Lasten gibt. Die Bewegungsgleichungen für freie Vibration können dann folgendermaßen geschrieben werden:
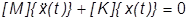
Nehmen wir an, wir haben eine sinusförmige Vibration, bei der die Verschiebung wie folgt beschrieben werden kann:
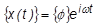
Ersetzen Sie den Term {x(t)} mit dem Inhalt der obenstehenden Gleichung ubd berücksichtigen Sie, dass bei einer sinusförmigen Abweichung die Beschleunigung gleich der zweiten Ableitung der Verschiebung ist:
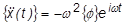
Das ergibt die folgende Bewegungsgleichung:
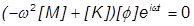
Da 
nie Null ist, kann die Gleichung in eine allgemeine Eigenwertgleichung umgeformt werden. Inventor Nastran bestimmt die Eigenfrequenz durch Lösen der Eigenwertgleichung:
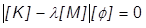
Dabei gilt:
[K] = globale lineare Steifigkeitsmatrix
[M] = globale Massenmatrix
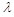= Eigenwert für jeden Modus, der die natürliche Frequenz = 
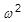ergibt
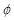= Eigenvektor für jeden Modus, der die natürlichen Modusform darstellt
Der Eigenwert bezieht sich auf die natürliche Frequenz des Systems:
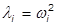
Dabei gilt:
= Kreisfrequenz (Radianten pro Sekunde)
oder in Hertz:
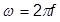
Dabei gilt:
f = zyklische Frequenz (Hertz)
Eine Lösung ist trivial (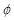 = 0), aber die anderen Lösungen für sind interessant. 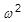wird Eigenwert genannt 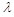und wird jeweils von einem eindeutigen 
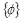, dem so genannten Eigenvektor, begleitet.
Durch Lösen der obigen Eigenwertgleichung erhält man genauso viele Eigenwerte und entsprechende Eigenvektoren wie Freiheitsgrade ohne Abhängigkeiten vorhanden sind. In der Praxis sind jedoch häufig nur die unteren Werte von Interesse. Diese Frequenz ist immer der erste Modus, der extrahiert wird.
Die Lösung der Eigenwertgleichung ist schwierig. Über die Jahre wurden mehrere unterschiedliche Ansätze entwickelt. Derzeit wird die Lanczos-Methode bevorzugt, da sie schnell, genau und robust ist. Darüber hinaus bietet Inventor Nastran Subspace-Methode. Sie kann in den seltenen Fällen verwendet werden, in denen die Lanczos-Methode fehlschlägt. SUBSPACE wird mit der Nastran-Direktive EXTRACTMETHOD=SUBSPACE im Dialogfeld Parameter unter Programmkontrollanweisungen ausgewäht (aktivieren Sie zuerst das Kontrollkästchen "Erweiterte Einstellungen"). Weitere Informationen finden Sie im Benutzerhandbuch unter dem Thema Parameter. Die vorgabemäßige Einstellung AUTO verwendent in den meisten Fällen Lanczos, wechselt aber bei einigen kleinen äAufgaben zu Subspace. Beachten Sie, dass Inventor Nastran die EIGR-Karte, die in andern Nastrans für die Verwendung anderer Extraktionsmethoden zur Verfügung steht, nicht erkennt.
Außerdem ist zwar der ermittelte Wert 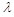der genaue Eigenwert, aber die Eigenvektoren wurdne willkürlich skaliert. Das bedeutet, dass die Vektoren keine eindeutige Größe haben. Sie stellen einfach nur eine Kontur dar. Vorgabemäßig führt Inventor Nastran eine Massenskalierung auf den Vektoren durch. Dies geschieht durch die Berechnung der verallgemeinerten Masse des Modells aus der Gleichung:
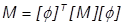
Dann werden alle Terme des Vektors durch diesen Wert geteilt. Das Ergebnis ist eine scheinbar willkürliche Skalierung der Vektoren. Es hat jedoch wichtige mathematische Eigenschaften, die an anderer Stelle genutzt werden können. Zusätzlich zur Massenskalierung, verfügt Nastran auch über eine Maximalskalierung, bei welcher der größte Wert im Vektor 1,0 beträgt. Damit können kleinere Vektoren manuell untersucht werden.
Eine Eigenschaft der Eigenvektoren ist ihre Orthogonalität. Dies bedeutet, dass ein Eigenvektor multipliziert mit eine anderen eine Identitätsmatrix ergibt. Ein Eigenvektor Vektor multipliziert mit sich selbst ergibt Null.
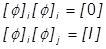
Dies ist eine weitere Eigenschaft, die bei Dynamik-Lösungen genutzt wird.
Modi für starre Körper
Basierend auf den Abhängigkeiten werden Modalanalysen normalerweise in zwei Typen unterteilt:
- Wenn das Modell keine Abhängigkeiten besitzt (z. B. eine Rakete oder ein Flugzeug im Flug), wird dies nach der entsprechenden Darstellung des Balken als Frei-Frei-Analyse bezeichnet. Das bedeutet, dass ein so analysierter Balken an beiden Enden frei wäre. Wenn bei einem Frei-Frei-System eine Modalanalyse durchgeführt wird, werden neben den Elastikmodi sechs Starrkörpermodi (bzw. Mechanismusmodi) mit einer Frequenz von 0 gefunden. Diese Modi repräsentieren die freie Translation und Rotation des Systems in die sechs Bewegungsrichtungen und werden als Modus eins bis sechs extrahiert. Modus sieben wird dann als erster flexibler Modus bezeichnet und ist kein Null-Energie-Modus. Es ist immer eine gute Modellüberprüfung, eine Modalanalyse ohne Abhängigkeiten auszuführen, um sicherzustellen, dass diese Modi gefunden werden. So wissen Sie, dass das das Modell nicht versehentlich eine interne Abhängigkeit beinhaltet. Manche Systeme haben tatsächlich keine Abhängigkeiten, und im Gegensatz zu einer statischen Analyse kann eine Modalanalyse bei einer Frei-Frei-Struktur erfolgreich ausgeführt werden.
- Die anderen Art der Modalanalyse ist ein abhängiges System. In diesem Fall sollte es keine Null-Frequenzmodi geben. Wenn sie dennoch gefunden werden, ist diesein Hinweis darauf, dass ein Teil des Modells sich frei wie ein Starrkörper bewegen kann. Dieser Bewegungstyp wird in der Regel als Mechanismus bezeichnet. Eine Modalanalyse kann derartige Probleme lösen, während eine statische Analyse schlägt fehlschlägt. Aus diesem Grund wird eine Modalanalyse häufig als Hilfsmittel zur Fehlerbehebung bei einer fehlgeschalgenenen statischen Analyse genutzt. Wenn die Quelle des Nullfrequenzmodus gefunden ist, kann dafür eine Abhängigkeit geschaffen und eine statische Analyse erfolgreich ausgeführt werden.
Mechanismusmodi treten bei Strukturen mit unzureichenden Abhängigkeiten auf, wenn ein Teil der Struktur sich als Starrkörper verschiebt. Ein Beispiel hierfür wäre eine flache Platte auf einem Scharnier oder ein Kugelgelenk. Ein Mechanismusmodus kann auch auftreten, wenn zwei Teile einer Struktur nicht richtig verbunden sind. Ein gängiges Beispiel hierfür ist ein Sgab, der mit einem Volumenkörperelemente verbunden ist.
Starrkörper- und Mechanismusmodi sind an Eigenwerten mit einer Frequenz von Null oder fast Null. Bei den meisten Strukturen sollte ein Wert nahe Null sich im Bereich von 1,0E-3 Hz oder weniger bewegen und kann negativ sein.
|
Vorheriges Thema: Dynamische Analyse |
Nächstes Thema: Modalanalyse – Übung |