Una vez que ha definido estas opciones, se aplican a Simulación dinámica hasta que se cambien. Defina las opciones inmediatamente después de abrir Simulación dinámica.
- En la cinta de opciones, haga clic en la ficha Entornos
panel Iniciar
Simulación dinámica para visualizar los paneles de simulación dinámica.
- Luego, haga clic en la ficha Simulación dinámica
panel Administrar
Configuración de simulación
.
- Pulse Convertir automáticamente restricciones en uniones estándar para activar el convertidor automático de simulación dinámica (motor de reducción de restricciones o CRE).
Por defecto, la opción está activada.
Al pulsar Aceptar, el CRE convierte automáticamente las restricciones del ensamblaje en uniones estándar y actualiza las uniones convertidas la próxima vez que se abre el mecanismo.
- Si desea que se le avise cuando se haya sobrerrestringido un mecanismo, pulse Advertir cuando el mecanismo esté sobrerrestringido.
Aunque este ajuste es el que se utiliza por defecto en los mecanismos nuevos, no está activado por defecto en los mecanismos creados con versiones anteriores a la 2008. Si activa esta opción y el mecanismo está sobrerrestringido, el software muestra un mensaje tras pulsar Aceptar y antes de crear las uniones estándar automáticamente.
- Si quiere obtener una indicación visual de los componentes incluidos en los distintos grupos móviles, seleccione la casilla de verificación Colorear grupos móviles. Las modificaciones de color por defecto se asignan a los componentes del mismo grupo móvil. Esta opción ayuda a analizar las relaciones entre los componentes. Para devolver los componentes a sus colores asignados por defecto, desactive la casilla de verificación del cuadro de diálogo o pulse el nodo Grupos móviles con el botón derecho y seleccione Colorear grupos móviles
- Pulse Todas las posiciones iniciales a 0,0
si desea definir todas las posiciones iniciales del grado de libertad en 0 sin cambiar la posición actual del mecanismo.
Esto resulta útil para ver los trazos variables que comienzan en 0 en el gráfico de salida de datos.
- Pulse Restablecer todos
para restablecer todos los sistemas de coordenadas en sus posiciones iniciales dadas durante la construcción del
sistema de coordenadas de de la unión .
Éste es el ajuste por defecto.
- Pulse
Análisis de tensión AIP para preparar toda la información CEF para el análisis en Análisis de tensión de AIP.
Esta función guarda los datos relevantes de CEF en los archivos de pieza de las piezas seleccionadas.
- Otra alternativa es pulsar
Simulación ANSYS para preparar un archivo con toda la información CEF para exportarla a ANSYS.
Esta función guarda los datos relevantes a CEF en un archivo legible para ANSYS.
- En el cuadro de entrada de texto, introduzca el nombre del archivo de información de CEF que se exportará a ANSYS.
- También puede pulsar Guardar en para especificar un archivo existente o crear un archivo.
Si selecciona un archivo existente, el software sobrescribe los datos que contiene el archivo.
Nota: Si utiliza la versión 10 u 11 de Ansys Workbench, debe hacer otra modificación en el archivo. Abra el archivo de texto, localice la sección llamada “Inertial State.” En esta sección, hay dos líneas que debe eliminar. Las líneas son “Grounded” y su código asociado, bien un “0” o un “1” en la línea siguiente.
- Pulse
Más para ver más propiedades.
- Para mostrar la información de copyright en archivos AVI, pulse Mostrar copyright en AVIs e introduzca la información en el cuadro de entrada de texto.
- Pulse Velocidad angular de entrada en rpm para introducir las velocidades angulares en rpm.
Sin embargo, la salida se localiza en las unidades que se definen cuando selecciona el archivo de ensamblaje vacío.
- Para definir la longitud del eje Z del sistema de coordenadas del ensamblaje para estructuras 3D en la ventana gráfica, introduzca el valor del porcentaje en el cuadro de edición de tamaño del eje Z.
Por defecto, el tamaño del eje Z es igual al 20% de la diagonal del cuadro delimitador.
- Pulse Aceptar o Aplicar.
Ambos guardan los parámetros, pero Aceptar también cierra el cuadro de diálogo.
Modelo de micromecanismo
Esta opción está diseñada para su uso en mecanismos con propiedades másicas pequeñas.
En el modo estándar, el cálculo falla si la masa o la inercia son inferiores a 1e-10 kg o 1e-16 kg.m2. Las ecuaciones dinámicas se resuelven con un procedimiento gaussiano, y con la precisión establecida en 1e-10 (por debajo de este valor, el giro se establece en 0).
Si el modelo de micromecanismo está activado, la masa o la inercia deben ser superiores a 1e-20 kg y 1e-32 kg.m2. La precisión gaussiana se establece en 1e-32.
Para saber cuándo activar esta opción, compruebe las propiedades másicas suministradas por el sistema de coordenadas de la unión.
- Si existe un grado de libertad de traslación, debemos comprobar la masa.
- Si existe un grado de libertad de giro en el eje X, debemos comprobar la inercia principal Ixx en el eje X, no las inercias cruzadas Ixz e Ixy, ya que no interesan en este momento.
|
Ejemplo 1 |
|
| En un mecanismo en el que la pieza más pequeña tiene una masa m = 6,5e-9 kg e inercias principales Ixx = 1e-20 kg/m2, Iyy = 1e-20 kg.m2, incluso si Izz > límite de inercia = 1e-10 kg.m2: | |
|
|
Precisión de ensamblaje
Se aplica únicamente a bucles cerrados y uniones de contacto 2D.
Contacto 2D: define la distancia máxima permitida entre puntos de contacto. El valor por defecto es 1e-6m = 1μm.
- Esta distancia siempre se comprueba al final de los pasos Runge-Kutta.
- Si la distancia entre los puntos no supera la precisión del ensamblaje, se aceptan las posiciones y las velocidades, y el cálculo prosigue con los errores de integración.
- Si la distancia supera la precisión del ensamblaje, se corrigen las posiciones hasta que deje de superar el valor de precisión. Seguidamente, en función de las nuevas posiciones, se corrigen las velocidades y el cálculo prosigue con los errores de integración.
Bucle cerrado: igual que el Contacto 2D, pero también puede tener restricciones angulares (expresadas en radianes) basadas en el tipo de unión.
- Las restricciones de distancia y angulares se comprueban al final de los pasos Runge-Kutta.
- Si las restricciones de distancia no superan la precisión del ensamblaje, y si las restricciones angulares tampoco superan la precisión del ensamblaje multiplicada por 1e3 (la precisión del ensamblaje expresada en metros), se aceptan las posiciones y las velocidades, y el cálculo prosigue con los errores de integración.
- En caso contrario, se corrigen las posiciones hasta que las restricciones de distancia no superen la precisión del ensamblaje y hasta que las restricciones angulares no superen la precisión del ensamblaje multiplicada por 1e3. Seguidamente se corrigen las velocidades y el cálculo prosigue con los errores de integración.
Modificación de la precisión del ensamblaje
El parámetro Precisión de ensamblaje puede modificarse en los siguientes casos:
- El mecanismo no se puede ensamblar al comienzo de la simulación o durante el proceso. En primer lugar, compruebe la viabilidad del mecanismo (la posición realista solicitada ejecutable por el mecanismo. Compruebe los movimientos impuestos que puedan tener como resultado posiciones contradictorias). Si no se detecta ningún problema y si la escala del mecanismo es grande (del orden de 1 m), aumente la precisión del ensamblaje (1e-5m o 1e-4m). Si la escala es pequeña (menos de 10 mm), reduzca la precisión del ensamblaje (1e-7m o 1e-8m).
- En casos donde el mecanismo sea inferior a 1 mm, reduzca la precisión del ensamblaje (en el rango 1e-8m/1e-10m) o utilice el modelo de micromecanismo.
Precisión de solucionador
Las ecuaciones dinámicas se integran mediante un esquema de integración de Runge-Kutta de quinto orden. El error y el paso de tiempo de la integración se gestionan del modo siguiente para poder ofrecer garantías:
- Se calcula el error de integración al final de cada paso de Runge-Kutta, en función de las velocidades y las aceleraciones calculadas.
- Este error de integración se compara con el parámetro “precisión de solucionador” definido por el usuario.
- Si el error de integración no supera la precisión del solucionador, el paso se acepta y la integración continúa.
- Si el error de integración supera la precisión del solucionador, se rechaza el paso. Entonces se calcula un nuevo paso de tiempo inferior al paso real y se reinicia la simulación desde el principio del paso con el nuevo valor del paso de tiempo.
El error de integración se calcula utilizando determinadas propiedades de las fórmulas de Runge-Kutta. Permite calcular fácilmente las posiciones “p” y las velocidades “v” de quinto orden (vectores con notación “p5” y “v5” respectivamente) y de cuarto orden (vectores con notación “p4” y “v4”). El error de integración se define en las posiciones y en las velocidades del modo siguiente:
|
Integ_error_position = norm(p5 - p4) Integ_error_velocity = norm(v5 - v4) Donde norm indica una norma especial. |
Cuando se acepta un paso, se establecen las siguientes relaciones (en unidades métricas):
|
Integ_error_position = norm(p5 - p4) < Atol + | p5 | . Rtol Integ_error_velocity = norm(v5 - v4) < Atol + | v5 | . Rtol |
Con:
| Atol | Rtol | |
|---|---|---|
|
Grado de libertad de traslación |
Precisión de solucionador Por defecto = 1e-6 Sin valor máximo |
Precisión de solucionador Por defecto = 1e-6 Sin valor máximo |
|
Grado de libertad de giro |
Precisión de solucionador 1e3 Por defecto = 1e-3 Valor máximo = 1e-2 |
Precisión de solucionador 1e3 Por defecto = 1e-3 Valor máximo = 1e-2 |
Para ilustrar este proceso, considere los siguientes ejemplos:
|
Ejemplo 1: ilustración de un error relativo para Rtol |
|
|
Tipo de unión: unión deslizante 1 con posición y velocidad |
|
|
p[1] = 4529.289768 m v[1] = 18.45687455 m/s |
|
|
Si la precisión del solucionador se establece en 1e-6 (valor por defecto), se garantizan resultados de seis dígitos: |
|
|
p[1] = 4529.28 m v[1] = 18.4568 m/s |
|
|
Si la precisión del solucionador se establece en 1e-8, se garantizan ocho dígitos: |
|
|
p[1] = 4529.2897 m v[1] = 18.456874 m/s |
|
|
Ejemplo 2: ilustración de un error relativo para Atol |
|
|
Tipo de unión: unión deslizante 1 con posición y velocidad |
|
|
p[1] = 0.000024557 m v[1] = 0.005896476 m/s |
|
|
Si la precisión del solucionador se establece en 1e-6 (valor por defecto), se garantizan resultados de seis posiciones decimales: |
|
|
p[1] = 0.000024 m v[1] = 0.005896 m/s |
|
|
Si la precisión del solucionador se establece en 1e-8 (valor por defecto), se garantizan resultados de ocho posiciones decimales: |
|
|
p[1] = 0.00002455 m v[1] = 0.00589647 m/s |
|
| El mismo razonamiento se aplica a las uniones de pasador, pero Atol y Rtol tienen una precisión de solucionador multiplicada por 1e3: | |
|
Ejemplo 3: ilustración de un error relativo para Rtol |
|
|
Tipo de unión: unión de pasador 2 con posición y velocidad |
|
|
p[2] = 12.53214221 rad v[2] = 21.36589547 rad/s |
|
|
Si la precisión del solucionador se establece en 1e-6 (valor por defecto), se garantizan resultados de tres dígitos: |
|
|
p[2] = 12.5 rad v[2] = 21.3 rad/s |
|
|
Si la precisión del solucionador se establece en 1e-8, se garantizan cinco dígitos: |
|
|
p[2] = 12.532 rad v[2] = 21.365 rad/s |
|
El parámetro Precisión de solucionador puede modificarse en los siguientes casos:
- La simulación se detiene con un mensaje de error y el paso de tiempo es lo suficientemente pequeño para garantizar resultados de calidad. Si hay pequeños desplazamientos, reduzca la precisión del solucionador. Si hay grandes desplazamientos, aumente la precisión del solucionador.
- Cuando se activan contactos 2D (estado = 1). Si hay pequeñas fuerzas, reduzca la precisión del solucionador. Si hay fuerzas grandes, aumente la precisión del solucionador. No es válido para fuerzas en momentos de impacto.
- Cuando se trabaja con mecanismos pequeños (inferiores a 1 mm). En estos casos, reduzca la precisión del solucionador o seleccione la opción Modelo de micromecanismo.
Velocidad de captura
Este parámetro se utiliza para simular impactos entre objetos. Ayuda al solucionador a limitar el número de rebotes previos a los resultados del contacto. El modelo de impactos utiliza un coeficiente de restitución “e”. El valor lo especifica el usuario y puede variar entre 0 y 1. En estas condiciones, los valores se tratan del modo siguiente:
- Cuando e = 0, se produce una disipación máxima de energía. Por ejemplo, tomemos el caso de un balón que cae sobre un plano desde una altura inicial, sin velocidad inicial y con efecto de la gravedad: no se observa rebote y el estado del contacto es = 1.
- Cuando e = 1, no se produce disipación de energía. Siguiendo con el ejemplo del balón, éste rebota hasta su posición inicial y el estado del contacto es = 0.5. El movimiento es periódico y prosigue hasta el infinito.
- Cuando e>0 y e<1, se produce disipación de energía en cada impacto. Sin dejar el ejemplo del balón, éste rebotará, pero la altura del rebote se reduce tras el primer impacto hasta llegar al límite. Entonces el balón permanece parado en el plano y el estado del contacto es = 1. Con estas condiciones puede utilizarse la velocidad de captura.
El parámetro Velocidad de captura ayuda al solucionador a limitar el número de pequeños rebotes que se producen antes de que el contacto se considere activo o constante. El proceso de captura se produce del modo siguiente:
- Se calcula el impacto con todos los coeficientes de restitución establecidos en sus valores iniciales.
- Las velocidades relativas al postimpacto, que representan las velocidades de recuperación, se comparan con el parámetro de velocidad de captura en todos los contactos.
- Si todas las velocidades relativas son cero o mayores que la velocidad de captura, se acepta el impacto y el solucionador avanza en el tiempo con las nuevas velocidades como parámetros iniciales.
- Si una velocidad relativa es inferior a la velocidad de captura y no es cero, se impone e = 0 para que dicho contacto pueda maximizar la pérdida de energía y se vuelve a calcular el impacto. Si se acepta el impacto, todos los coeficientes de restitución se restablecen en sus valores iniciales.
¿Cuándo se puede modificar el parámetro?
Este parámetro se puede modificar en el siguiente caso:
- Cuando se tienen contactos 2D y la simulación es lenta. Detenga la simulación y trace la velocidad de captura. Si el parámetro varía en cada paso de tiempo (entre 0 - 1 - 2) o si es igual a 1, se produce un error de captura. El solucionador intenta estabilizar el estado de los contactos, pero es un proceso largo y complicado. En este caso, aumente la velocidad de captura.
- Reducir el valor del parámetro no supone ninguna ventaja.
Velocidad de regularización
En los contactos 2D, se utiliza una ley de fricción real no lineal de Coulomb. En las uniones y los contactos 3D, por simplicidad y para evitar estados hiperestáticos, se utiliza una ley regularizada de Coulomb y se puede ilustrar del modo siguiente:
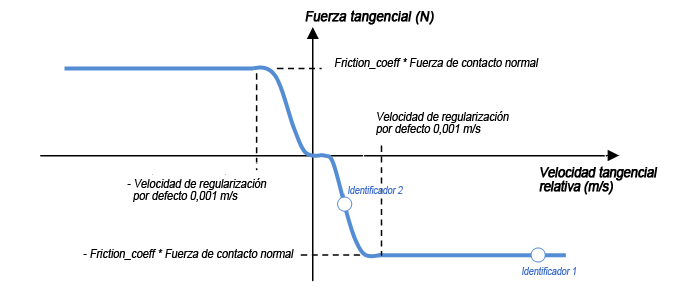
La regularización viene definida por el parámetro de regularización de velocidad.
Con este modelo, en casos de contacto de fijación (o contacto de rodillo), si la velocidad tangencial relativa es cero, la fuerza tangencial es nula.
En el caso de la fricción de uniones en un grado de libertad de giro, la fuerza tangencial se sustituye por un par de torsión tangencial (unidad: Nm) y la velocidad relativa tangencial es una velocidad de giro (unidad: rad/s). Ambas se calculan multiplicando la fuerza tangencial y dividiendo la velocidad de traslación por el radio de la unión.
|
Ejemplo 1 |
|
|
Una unión de pasador con un radio de 10 mm se dirige con una velocidad constante “w” de 10 rad/s. Aplicamos una fuerza (Fn) de 20 N a la unión, perpendicular a su eje de rotación, y definimos un coeficiente de fricción (mu) de 0,1. En este caso, el par de fricción (Uf) de la unión se puede calcular del modo siguiente: |
|
|
? = r * w = 0.01 * 10 = 0,1 m/s ? > velocidad de regularización = 0,001 m/s => Uf = -mu * r * Fn = -0,1 * 0,01 * 20 = -0,02 Nm Véase “etiqueta 1” en el gráfico regularizado de Coulomb. |
|
|
Ejemplo 2 |
|
|
Seguimos con el mismo ejemplo, pero con una velocidad (w) de 0,05 rad/s, el par de fricción (Uf) viene determinado por: |
|
|
? = r * w = 0,01 * 0,05 = 0,0005 m/sm ? > velocidad de regularización = 0,001 m/s => Uf ≈ -mu * r * Fn/2 = -0,1 * 0,01 * 20/2 = -0,01 Nm Véase “etiqueta 2” en el gráfico regularizado de Coulomb. |
|
El parámetro Velocidad de regularización puede modificarse en los siguientes casos:
- La simulación es lenta y se producen pequeñas oscilaciones en una unión con fricción o en una unión de contacto 3D. La fricción de la unión o del contacto 3D crea una rigidez considerable en el modelo, por lo que el solucionador reduce el paso de tiempo para asegurar una precisión fiable. Debe reducir la rigidez => aumentar el parámetro Velocidad de regularización en un factor de 5 (5e-3 m/s). Si el modelo sigue siendo lento, puede aumentar más el parámetro con valores relacionados con el modelo (inferiores a las velocidades del modelo).
- No aumente mucho la velocidad de regularización; en caso contrario, sólo funcionará entre dichos valores. La fuerza de fricción nunca alcanzará su valor máximo. El resultado es un límite artificial en el efecto de la fricción.
Validación numérica
Antes de analizar los resultados de la simulación, es importante comprobar que la simulación es válida desde un punto de vista numérico, es decir, que no depende de parámetros numéricos. Para llevar a cabo el paso de validación numérica, realice lo siguiente:
- Ejecute una simulación con un conjunto de parámetros numéricos (precisión de solucionador y de ensamblaje, velocidad de captura, velocidad de regularización y paso de tiempo) y, a continuación, guárdela.
- Divida cada parámetro por 10, ejecute la simulación y guárdela.
- Trace todos los resultados en el mismo gráfico. Si los resultados se parecen, la simulación no depende de parámetros numéricos. Si no se parecen, existe un problema.
- Si la simulación no depende de parámetros numéricos, puede analizar los resultados.
- Si depende de parámetros numéricos, utilice las curvas resultantes para determinar qué parámetro provoca el problema. Divida este parámetro por 10 y tome el valor resultante como valor nominal del parámetro numérico. Reinicie la validación desde el principio. Para ahorrar tiempo, puede validar la dependencia de un solo parámetro.