Las estructuras de cable son estructuras cuyos principales elementos para la transferencia de cargas son los cables. Si una de las dimensiones principales de un elemento es mayor que las dos restantes y la rigidez de la sección con respecto a la flexión y la torsión es pequeña en comparación con la rigidez de la tensión, dicho elemento se considera un cable.
La conclusión básica que se extrae de la definición anterior es que solo se pueden aplicar esfuerzos de tracción a los cables. Sin embargo, en algunos casos, se pueden aplicar pequeños momentos de flexión o torsión y esfuerzos cortantes a los cables. La ventaja más significativa del uso de estructuras de cable es que los cables admiten tensiones de tracción elevadas.
Por lo tanto, puede utilizar una sección de cable para diseñar estructuras ligeras, económicas y estéticas. Existen dos ventajas al utilizar elementos de cable en las estructuras diseñadas:
- La introducción de la tensión inicial del cable regula el esfuerzo interno y hace que los resultados sean más efectivos.
- El ensamblaje es sencillo (por ejemplo, la suspensión y montaje de toda una estructura, debido a su menor peso).
La teoría de las estructuras de cable se basa en los siguientes supuestos:
- Las cargas y otros efectos externos son de tipo cuasiestático y son constantes en el tiempo.
- Para los cables, no se tienen en cuenta los momentos flectores ni los esfuerzos cortantes.
- Los elementos de cable funcionan en el rango elástico (módulo de Young E = const).
- Se puede aplicar cualquier carga, excepto cargas de momento.
- Se permiten grandes desplazamientos u, pero gradientes pequeños du/dx.
- El área de sección de cable F es constante (F=const).
- Longitud de cable sin carga = l.
Ecuaciones que rigen el problema
Pensemos en un cable con poca caída (es decir, un cable en el que el ángulo entre la tangente de cualquier punto del cable y la línea recta que une sus extremos es pequeño) con una carga arbitraria en su plano. Pensemos en un elemento infinitesimal en este cable que se describe en la fase inicial (la primera fase, de ensamblaje) mediante la carga q0, la temperatura T0 y la tensión H0; la longitud de este elemento es igual a dso (Fig. 1a). Una vez que la carga se ha aplicado al cable (la segunda y última fase con la carga q, temperatura T y tensión H), la longitud de una sección elemental de cable es igual a ds (Fig. 1b). Ambas fases, junto con las cargas en ambos planos (xy y xz), también se muestran en la figura 2.
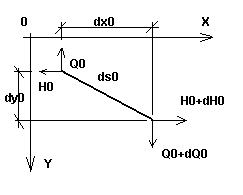 Fig. 1a |
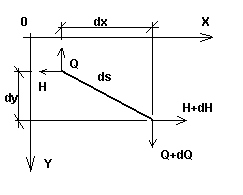 Fig. 1b |
Si damos por hecho que el valor de caída del cable es pequeño y tenemos en cuenta que el esfuerzo total del cable debe ser tangente al mismo, se puede asignar la prolongación de cable adecuada como una función de solo valores estáticos. Una vez realizada la integración a lo largo de la longitud total del cable, se obtiene la fórmula conocida para un cable con un valor de caída pequeño. El valor D de la prolongación del cable se puede derivar de (1).
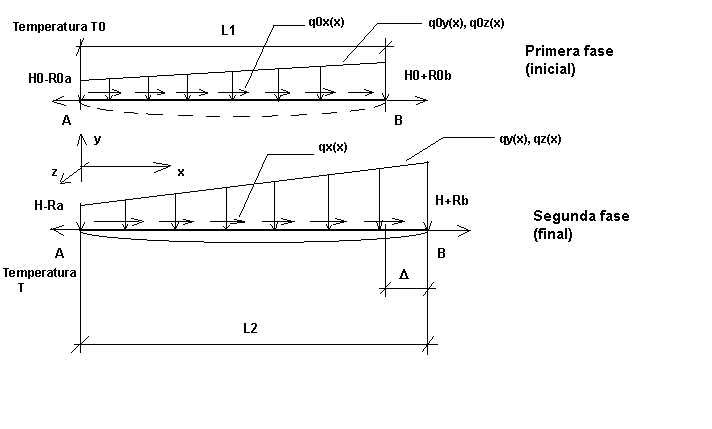
Fig. 2
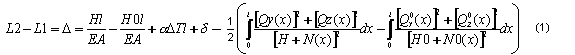
donde:
A, B: nudo inicial y final del cable.
EF: rigidez de la tensión del cable (donde E: módulo de Young, F: área de sección transversal del cable).
a: coeficiente de expansión térmica.
l: longitud inicial del cable (para cable sin carga).
D: cambio de distancia entre apoyos.
d: reducción/prolongación inicial interna del cable (regulación)
DT: cambio de temperatura
Q(x): función de esfuerzo cortante para una viga con apoyos articulados (según los índices: respectivamente en las direcciones del eje Y y Z y para la fase inicial y final). Consulte la figura 3a.
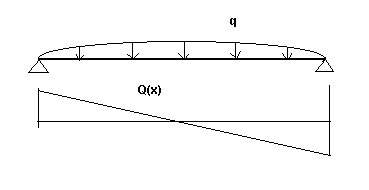
Fig. 3a
N(x): función de esfuerzo axial causado por la carga estática de una viga con apoyos empotrados (durante la fase inicial o final). Consulte la figura 3b.
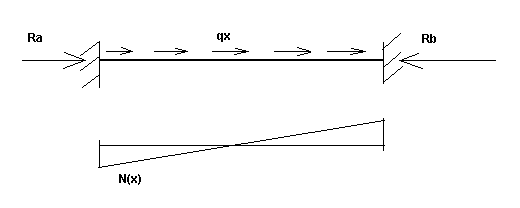
Fig. 3b
También puede observar que en la ecuación de cable (1), a diferencia de las soluciones tradicionales aplicadas a los cálculos de cables, el esfuerzo axial puede variar a lo largo del cable (en los denominadores de ambas funciones de integración de la ecuación (1), existen los siguientes componentes funcionales: [H+N(x)] 2 y [H0+N0(x)] 2 ). Esto permite obtener resultados más precisos.
Consulte también:
Observaciones prácticas sobre los cálculos de estructuras de cable