La teoría de elementos de cable en Robot se basa en la teoría general de cables con un valor reducido de cable cóncavo. Según esta teoría, la rigidez del cable es una función implícita de los siguientes parámetros: rigidez de tensión del cable (E*F), tensión del cable, desplazamientos del apoyo del cable y carga transversal en ambas direcciones (p y , p z ).
Debido a la no linealidad del elemento de cable, su definición en la estructura requiere la aplicación de métodos repetitivos de análisis de estructura.
Funciones de implementación de cables en Robot:
- Los elementos de cable se pueden utilizar junto con elementos de los siguientes tipos de estructura: PÓRTICO PLANO, PÓRTICO ESPACIAL y LÁMINA.
- Se permiten todos los tipos de análisis de estructura estándar: lineal (de hecho, es un análisis no lineal, pero no se tienen en cuenta otros efectos no lineales, excepto la no linealidad de los elementos de cable), no lineal (con respecto al efecto de rigidizador de tensión), P-Delta, incremental, pandeo, dinámico, armónico y sísmico. Nota: El análisis dinámico se considera lineal con respecto a la rigidez actual.
- Se admiten excentricidades.
- El material se define como para una barra (el módulo E de Young es el único requisito en el caso de una definición de peso propio de cable; además, debe introducirse el peso unitario, RO, y, en el caso de una carga térmica, el coeficiente de dilatación térmica LX)
- Ángulos GAMA definidos como para barras (es importante solo para la descripción de la carga).
Limitaciones:
- Para los elementos de cable, es imposible definir una relajación, ya que la rigidez de flexión y torsión no se aplica a esos elementos.
Cargas de cable
Los siguientes tipos de carga se aplican a los elementos de cable:
- Cargas sobre los nudos
- Pesos propios
- Cargas uniformes (constantes o variables)
- Recorte/alargamiento inicial (cargas adicionales aplicadas durante la fase de montaje)
- Carga térmica
- Fuerzas concentradas a lo largo de la longitud del elemento
Los siguientes tipos de carga no se aplican a los elementos de cable:
- Momento
- Momento uniforme
SINTAXIS (que debe introducir un usuario en un archivo de texto)
CARActerísticas
(<lista de elementos>) CABles AX=<área de sección> (E=<módulo de Young>)
(RO=<peso unitario>) [TENsión = <s> | FUErzas = <h> | LONgitud = <l>
| [ DILatacion = <d> (RELativa) ]]
donde:
TENsión: tensión normal (calculada respecto al cordón) que se debe conseguir para el caso de carga de montaje.
FUERza: fuerza de tracción (calculada respecto al cordón) que se debe conseguir para los casos de carga de montaje.
LONgitud: longitud inicial del cable.
DILatacion: diferencia entre la longitud inicial del cable y la distancia entre los nudos de apoyo. (Si es un valor positivo, la longitud es mayor que la distancia entre los nudos; si es negativo, la longitud es menor que la distancia entre los nudos).
DILatacion RELativa: relación de la diferencia entre la longitud inicial del cable y la distancia entre los nudos de apoyo. (Si es un valor positivo, la longitud es mayor que la distancia entre los nudos; si es negativo, la longitud es menor que la distancia entre los nudos).
- El módulo E de Young se puede establecer en la definición del material.
- Palabras clave: TENsiones, FUErza, LONgitud y DILatacion se definen explícitamente y no son necesarias. Si no se especifica ninguno de estos parámetros, la longitud inicial del cable es igual a la distancia entre los nudos.
Caso de carga de montaje
Robot incluye la fase de montaje de la estructura. Es recomendable que este sea el primer caso de carga. A continuación, se ofrece la sintaxis para este caso de carga:
CASo
MONtaje
[descripción de carga]
En este caso de carga:
- Para las barras seleccionadas, las fuerzas de tracción iniciales se especifican introduciendo uno de los valores siguientes en una sintaxis de archivo de texto (comando CARActerísticas):
TENsión = s0 (tensión de cable inicial)
FUERza = t0 (fuerza de tracción inicial en el cable)
- La longitud inicial del cable se puede describir especificando LONgitud = l
0
, si se desea que sea diferente del valor por defecto LONG =
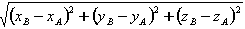, que es igual a la distancia entre los nudos. - El acortamiento/alargamiento inicial del cable se puede especificar mediante el comando DILatacion (RELativa).
- Si no se especifica la palabra clave RELativa, DILatacion se expresa en valores absolutos.
- Si se especifica la palabra clave RELativa, el alargamiento inicial se expresa como una fracción, es decir, la longitud final del cable es igual a L = LONG (1 + DIL).
- Se aplican todas las cargas definidas (como, por ejemplo, pesos propios y masas añadidas).
- Se permite la definición de temperatura TX para los cables en la fase de montaje.
- Los desplazamientos calculados para este caso de carga describen la geometría inicial para los casos restantes del análisis de estructura.
Durante el análisis de casos sucesivos de carga de la estructura en el estado de equilibrio, se tienen en cuenta las cargas del caso de montaje aplicadas a la estructura. Los desplazamientos asignados a este caso se utilizan como base para un análisis posterior. Las fuerzas de tracción predefinidas se modifican, lo que significa que, después del montaje, el cable se ancla.
Ecuación de cable para la fase de montaje
En esta fase, la ecuación (1) describe la transición desde:
- Cable sin carga (cable en el suelo):
q0x = q0y = q0z = 0 (sin carga)
H0 = 0 (sin tensión de cable)
T0 = 0
para el que la longitud es igual a L1= :
1.
largo, cuando (largo ≠ 0); si el valor LONgitud se especifica en una definición de cable.
2.
[distancia (A, B) + dilatación], cuando la dilatación se define en un sistema absoluto, si el valor DILatacion se especifica en una definición de cable.
3.
[distancia (A, B)*(1+dilatación)], cuando la dilatación se define en un sistema relativo; si el valor DILatacion RELativa se especifica en una definición de cable.
4.
[distancia (A, B)], cuando (dilatación = 0) y (largo = 0); si no hay ninguna palabra clave como LONgitud, DILatacion o DILatacion RELativa en una definición de cable o está presente una de las siguientes palabras clave: FUErza o TENsión.
a
- cable anclado en la estructura con todas las cargas del primer caso de carga (montaje):
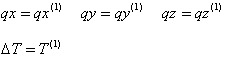
L2: Distancia entre los nudos de apoyo A y B del cable deformado:
L2 = distancia (A+U A , B+U B )
donde:
U A : desplazamiento del punto A
U B : desplazamiento del punto B
En el primer caso, se pueden dar diversas situaciones, como se indica a continuación:
- La fuerza H es conocida (controlada): si TENsión o FUErza (tensión) no son iguales a cero (TENsión≠0 o FUErza≠0). A continuación, la fuerza de tracción es igual a:
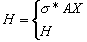
Desde la ecuación (1):
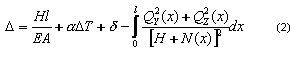
El valor l es la distancia entre los nudos inicial y final del cable.
Desde la ecuación (2), se puede asignar el alargamiento inicial del cable esencial para obtener la fuerza necesaria H:
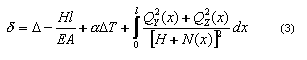
- No se conoce la fuerza de tracción H (no se especifican los valores TENsión ni FUErza en la sintaxis de cable), por lo que:
- Si se tienen en cuenta los desplazamientos durante la fase de montaje (definidos mediante la introducción de los valores LONgitud, DILatacion o DILatacion RELativa en la sintaxis de cable), es decir,
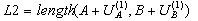
entonces, al resolver la ecuación (4) según la fuerza H
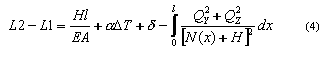
e iterar a través del sistema de ecuaciones, se obtiene el valor final de la fuerza de montaje.
Es igual a:
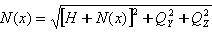. - Si no se tienen en cuenta los desplazamientos nodales, es decir,
L2 = longitud (A, B)
al resolver la ecuación (4), se obtiene el valor inicial de la fuerza necesaria para el anclaje de cable entre apoyos.
- Si se tienen en cuenta los desplazamientos durante la fase de montaje (definidos mediante la introducción de los valores LONgitud, DILatacion o DILatacion RELativa en la sintaxis de cable), es decir,
- La fuerza H es conocida (controlada): si TENsión o FUErza (tensión) no son iguales a cero (TENsión≠0 o FUErza≠0). A continuación, la fuerza de tracción es igual a:
Casos de carga después del anclaje
Una vez completado el análisis de la estructura, los resultados de los elementos de cable son similares a los obtenidos para los elementos de barra, aunque quedan algunas diferencias. Entre las diferencias, se incluyen las siguientes:
- No se pueden obtener fuerzas ni momentos de corte para elementos de cable.
- Para elementos de cable se puede obtener la deformación simplificada (asignada como para la barra de celosía) o la deformación exacta (descrita por la ecuación diferencial de la línea cóncava).
- Resultados adicionales para elementos de cable (como resultado de la fase de montaje):
- En los cables para los que se necesita tensión (en la sintaxis de Robot: TENsión o FUErza), se asigna el valor de regulación [m] necesario para la tensión requerida.
- En otros cables, se asigna la fuerza esencial para el montaje.
Estos resultados son útiles para diseñar la fase de montaje. Están disponibles en el módulo Resultados. Para ello, seleccione el comando Tensiones > Parámetros > Resultados para los elementos de cable en la fase de montaje.
- La fuerza axial (tracción) se calcula a partir de la fórmula:
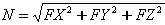
donde:
N: fuerza aplicada a lo largo de la tangente del cable.
FX, FY, FZ: componentes de fuerza N proyectados en direcciones de ejes sucesivos del sistema de coordenadas local.
Ecuación de cables durante el trabajo de cables en la estructura
Cuando se define un caso arbitrario (i) después del primer caso de montaje, el comportamiento de los cables se obtiene mediante la resolución de la ecuación (1). La iteración de una ecuación de este tipo se realiza según los siguientes supuestos:
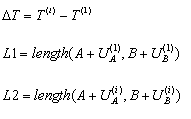
La carga del primer caso de carga se añade automáticamente a la carga en el caso (i).
La fuerza de tracción H se considera una cantidad desconocida.
Consulte también:
Observaciones prácticas sobre los cálculos de estructuras de cable