El análisis temporal obtiene la reacción de la estructura en los puntos de tiempo seleccionados para una interacción duradera definida. Esto es contrario a otros tipos de análisis disponibles que muestran la reacción de la estructura en forma de amplitudes obtenidas por un solo momento.
El análisis temporal consiste en encontrar una solución de la siguiente ecuación de la variable de tiempo "t":
M * a(t) + C * v(t) + K * d(t) = F(t)
donde se conocen los siguientes valores iniciales: d(0)=d0 y v(0)=v0,
donde:
M: matriz de masas.
K: matriz de rigidez.
C = a * M + b * K - matriz de amortiguamiento.
α: coeficiente definido por el usuario.
β: coeficiente definido por el usuario.
d: vector de desplazamiento.
v: vector de velocidad.
a: vector de aceleración.
F: vector de sobrecarga.
Todas las expresiones que contienen el parámetro (t) dependen del tiempo.
El método Newmark o el método de descomposición se utilizan para resolver la tarea anterior. El método Newmark pertenece al grupo de algoritmos que son incondicionalmente convergentes para los parámetros de método definidos de forma adecuada. Utiliza las siguientes fórmulas para calcular los desplazamientos y la velocidad en el siguiente paso de integración.
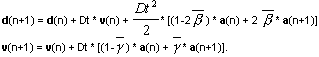
Los parámetros β y γ controlan la convergencia y la precisión de los resultados obtenidos mediante el método.
La convergencia incondicional está garantizada para 0.5 ≤ γ 2≤ * b.
Se adoptan los valores b = 0.25 y g = 0.5. Es posible modificar estos valores, pero solo si se utiliza el análisis temporal lineal con los métodos Newmark o Newmark (aceleración) activados. Estos valores (TransBeta y TransGamma) se pueden cambiar en el archivo de preferencias *.COV guardado en la carpeta CFGUSR. Para realizar cálculos para diferentes valores de los parámetros b y g, es necesario cambiar los parámetros TransBeta y TransGamma en el archivo *.COV, y cargar ese archivo de preferencias.
Se recomienda utilizar el método Newmark para historiales temporales cortos cuando se aplica una carga concentrada a la estructura. Estas cargas inducirán un movimiento que requerirá que se describa un gran número de modos propios. Por lo tanto, el método Newmark será más eficaz que el método de descomposición modal para este tipo de tarea. El método Newmark aprovecha las ecuaciones iniciales sin ninguna simplificación. La precisión de los resultados obtenidos depende de la precisión de la integración numérica de las ecuaciones de tiempo y se define mediante el valor del paso de tiempo de los parámetros seleccionadosα α, β. El método no requiere que se resuelva el problema de valores propios para obtener los valores propios y vectores propios. Sin embargo, para los historiales temporales prolongadas, el método requiere mucho tiempo. En el caso de estas tareas, los cálculos deben realizarse para un gran número de pasos de tiempo con la precisión necesaria.
El método Hilber-Hughes-Taylor (HHT) implementa el amortiguamiento numérico de frecuencias más altas sin perder precisión en la solución. A continuación, se muestra una forma discreta de la ecuación del historial de tiempo.
donde:
-1/3 ≤ ≤ 0
Suponiendo:
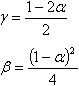
se obtiene un esquema de integración incondicionalmente estable con precisión de segundo orden.
Para el modo de aceleración, los valores de prueba en el paso n+1 de integración se determinan como se indica a continuación.
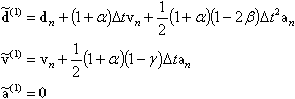
El método HHT es un algoritmo muy eficiente para la integración numérica que permite eliminar el impacto desfavorable de las frecuencias altas en la calidad de una solución.
El método de descomposición modal es un método sencillo para obtener la solución requerida. Se basa en la representación del movimiento de la estructura como una superposición del movimiento de las formas no acopladas. Por lo tanto, el método requiere que se determinen valores propios y vectores propios. Se recomienda el método Lanczos para este fin, seguido de la verificación de Sturm. El método de descomposición modal aprovecha las ecuaciones sin acoplar reducidas.
La ecuación (sin amortiguamiento) puede tener la siguiente forma:
donde
,
Ng: número de "grupos de carga", φk(t): historial de tiempo del grupo de carga k-th
(2)
Al insertar la ecuación (2) en la ecuación (1) y reconocer el amortiguamiento modal y las condiciones de ortogonalidad 
, se obtiene la siguiente ecuación.
donde 
, ξ - parámetros de amortiguamiento modal, ωi - frecuencia para la forma i-th.
Cada ecuación se resuelve numéricamente con la precisión del segundo orden. El vector de desplazamiento resultante X(t) para los puntos de tiempo definidos t* = t1, t2, ... se obtiene después de introducir qi(t*), i=1,2,...,m en las ecuaciones (2).
Cabe señalar las diferencias entre los tipos de análisis disponibles que se describen en este tema. El análisis del movimiento difiere del análisis temporal en que no reconoce los efectos dinámicos. La diferencia entre el análisis armónico y el análisis temporal consiste en que determina la reacción de la estructura exclusivamente en forma de amplitudes, y no en función del tiempo.
Consulte también: