周波数応答解析を使用して、定常状態の振動励起に対する構造の応答を計算します。周波数応答解析では、励振が周波数領域で明示的に定義されています。励振は、適用される力と強制される運動(変位、速度、または加速度)の形式にすることができます。
周波数応答解析には次の 2 つのタイプがあります。
- 直接周波数応答解析では、複雑な代数式を使用して一連の連成行列方程式を解くことで、不連続な励振周波数での構造の応答を計算します。周波数の高い励振に多数のモードの抽出が必要なモデルでは、直接解析の方が効率的な場合があります。
- モード周波数応答解析では、別の方法で周波数応答を計算します。この方法では、構造のモード形状を使用して運動の方程式を非連成化し(減衰がない場合、またはモード減衰のみを使用する場合)、計算され保持されたモードの数に応じて問題の規模を小さくします。これらの係数のどちらを使用しても、モード周波数応答解析の計算効率が直接周波数応答解析よりも高くなる傾向があります。多数の解析周波数が指定される大規模なモデルで、この解析方法が使用されます。この方法では、物理的な自由度(DOF)を、数を減らしたモードの自由度に置き換えます。自由度の数を減らすと、解析時間が短縮します。モード周波数応答解析は、構造のモード形状を使用するため、固有値解析を自然に拡張した解析です。
直接周波数応答理論
直接周波数応答解析は、運動の一般的な振動から開始しますが、振動荷重を次のように仮定します。
次の振動関数の形での解も提案できます。
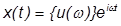
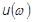は複雑な変位ベクトルです。速度と加速度は次の導関数を使って計算できます。
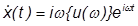
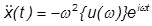
これを運動の方程式に代入して、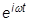
項で割ると次の式が得られます。
周波数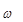 
はこの方程式では定数です。したがって解は、選択した各周波数での複雑な変位ベクトル u となります。
直接周波数応答解析では、選択した周波数ごとにこの方程式が繰り返し解かれます。その結果、解析時間は、解析で選択する周波数の数に比例します。
モード周波数応答理論
モード周波数応答解析を実行するには、物理的な座標をモード座標に変換する必要があります。固有振動数や固有ベクトルは、直交性という特性があるため、この変換に適しています。そのため、物理的な座標 u をモード座標に置き換えることができます。そこでまず、変換が次のように定義されます。
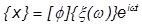
これが運動の方程式に代入されます(ここでは減衰項目を無視しています)。
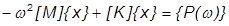
結果は次のようになります。
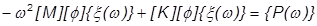
ここで、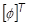
を左から掛けます。
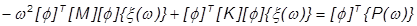
これらの項は、扱いが容易な非連成の一般成分に置き換えられます。
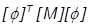= モードまたは生成された質量マトリックス
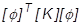= 剛性のモード行列または一般化行列
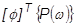= モード荷重ベクトル
この結果、容易に解が計算される一連の非連成方程式となります。
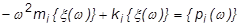
モード変位 
が分かると、次のようにモード変位の合計から物理的な変位を求めることができます。
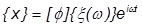
すべてのモードの自由度が変換に含まれている場合は、このアプローチで直接法とまったく同じ答えが出ます。ただし、物理的な自由度よりもかなり少ないモードの自由度を使用して、いつもほぼ正確な答えを取得できるため、このアプローチには強みがあります。DOF を少なくすると、解析の進行がかなり速くなります。これによって、大規模なモデルや、多数の周波数を持つモデルの場合に、特に効率的になる可能性があります。
|
前のトピック: モード回避の演習 |
次のトピック: 周波数応答解析の演習 |