Static forces applied to a structure influence the frequency of vibrations of the structure. The commonly used modal analysis (determining the vibrations of a structure) does not recognize the influence of static forces. To approximate the actual conditions in which a structure works, the calculations performed in Robot may be carried out according to modal analysis recognizing the applied static forces in modal analysis.
There are two stages of structure vibration calculations that recognize the operation of static forces. These analyses are of static correlation between stress and deformation under the influence of a defined static load.
Stage One: Linear
where:
xst - Unknown vector of the static state
b - Vector of a defined static load (static load vector)
K - Stiffness matrix
L (xst, b) - Non-linear operator.
The vector of static load b may be a simple load case or a combination of defined load cases.
Stage Two: Modal (Non-linear) Analysis
![]() , ( 2a )
, ( 2a )
where:
Ks - Stress stiffness matrix, originating from the stresses in the static state
M - Mass matrix
ωi2 - Eigenvalue (ωi = pulsation)
Φ - Eigenvector.
To solve a non-linear static problem (modal), one uses the same methods as in non-linear static analysis. For a linear static problem, the following correlation holds: ![]() , where G is a geometrical stiffness matrix.
, where G is a geometrical stiffness matrix.
Positive values ωi (ωi > 0) describe stable states of equilibrium, while negative values (ωi < 0) correspond to non-stable states of equilibrium. In turn, the zero value (ωi = 0) indicates lack of stability (buckling).
If the matrix K + Ks (xst) stops being positively determined, the static load approaches the critical value (buckling). During the analysis on the non-linear static problem (modal), convergence is not achieved. If the linear approach (a stage of static analysis) is selected and the matrix is not positively determined, it is recommended to stop calculation, as further calculations do not make any sense.
Example
Consider the example of the structure shown in the following drawing. N refers to a static load.
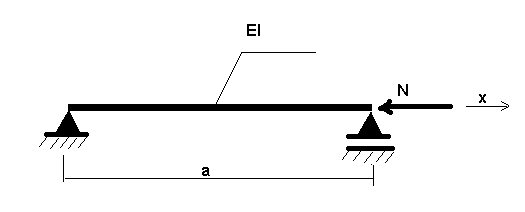
The following formula describes its behavior.
![]() , ( 3 )
, ( 3 )
where:
w - Displacements due to bending
ρ - Material density
F - Cross-section area.
The solution to this formula will by searched by means of the following formula:
![]() ( 4 )
( 4 )
Once the expression ( 4 ) is introduced into the formula ( 3 ), the following is obtained.
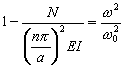 , ( 5 )
, ( 5 )
where:
![]() - buckling load
- buckling load
ω02 - Eigenvalue for N=0 result of the regular modal analysis).
After transforming the final formula, the following is obtained.
![]() , ( 6 )
, ( 6 )
where ω2 - Eigenvalue obtained for the structure undergoing the operation of the static load N.
The result of the above considerations is presented graphically in the following drawing.
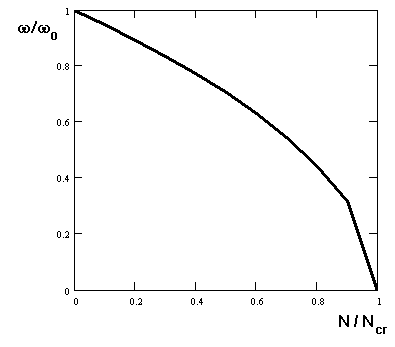
In conclusion, for actual structures the correlation ω= ω(b) is usually slightly more complex than that obtained from the formula (6).