Para refinar ainda mais o processo, uma elipse de erro padrão também pode ser desenhada. O uso de uma distribuição F de estatística aplicada, uma elipse de erro de probabilidade a 95% ou 99% é criada. Esta elipse tem arcos tangentes para os lados do retângulo de erro, com sua orientação determinada por um ângulo, T, e eixos UV ortogonais auxiliares. Novamente, os valores da matriz de covariância são usados para calcular o ângulo T e os semieixo maior e semieixo menor.
Primeiramente, resolva três variáveis para usar em equações que determinam os semieixo maior e semieixo menor: K, Quu e Qvv.
As seguintes fórmulas são usadas:
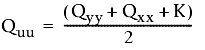
e
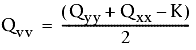
onde
- Qxx, Qyy e Qxy são valores da matriz de covariância.
Então, estes valores são utilizados para solucionar duas equações que determinam Su, o comprimento do semieixo maior e Sv, o comprimento do semieixo menor.
e
onde
- So = Desvio-padrão de peso unitário
Finalmente, o ângulo T, que o eixo U faz com o eixo Y, é resolvida através da seguinte equação:
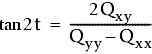
O ponto ajustado provavelmente está localizado dentro da elipse com um grau de confiança de 95% ou 99%.