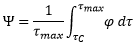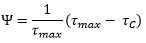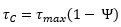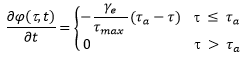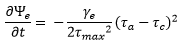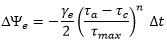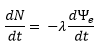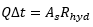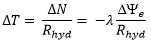L’analyse de la turbidité peut être utilisée comme outil de prévision des phénomènes de coloration de l’eau. Les résultats de l’analyse peuvent permettre d’élaborer des stratégies de purge dans le but d’améliorer la qualité de l’eau dans le réseau et de réduire les réclamations des clients.
Pour inclure une analyse de la turbidité dans une simulation de la qualité de l’eau, cochez l’option Effectuer l’analyse de la turbidité dans la boîte de dialogue Options de qualité de l’eau lors de la planification d’une exécution.
Pour en savoir plus sur les paramètres de modèle requis pour une analyse de la turbidité, voir la rubrique Paramètres de qualité de l’eau.
Des résultats supplémentaires sont disponibles lors de l’exécution d’une analyse de turbidité :
- Turbidité : turbidité au niveau du nœud
- Rapport de turbidité stockée : rapport entre la quantité de matière colorante et la quantité totale de cette matière fixée sur la paroi de la canalisation
- Pic de turbidité : valeur maximale de la turbidité dans tous les segments de la canalisation à la fin de la boucle temporelle relative à la qualité de l’eau
Détails techniques
Le modèle d’analyse de la turbidité d’InfoWorks WS s’appuie sur une adaptation de l’approche de modélisation de l’érosion et de la régénération de la matière colorante dans les systèmes de distribution d’eau publiée par Furnass et al. (2014).
Avec l’approche de Furnass et al (2014), la quantité de matière colorante fixée sur la paroi de la canalisation est représentée par une fonction d’état de la matière φ(θ, t), qui est en fait une fonction de répartition de la contrainte de cisaillement, définie comme la quantité relative de matière colorante fixée sur la paroi de la canalisation pour une contrainte de cisaillement donnée, θ.
Le processus de régénération a eu une influence plus importante sur cette approche que le processus d’érosion. Cependant, l’implémentation dans InfoWorks WS ne modélise que le processus d’érosion, car la régénération se produit sur une longue période de plusieurs mois ou années.
Avec l’approche de Furnass et al (2014), c’est le processus de régénération qui nécessite la fonction complète de répartition de la contrainte de cisaillement, mais il est utile de la conserver comme point de départ.
Avec l’érosion, nous sommes libres d’intégrer φ sur un intervalle approprié de θ. Si l’on note θC la valeur minimale de θ pour laquelle φ n’est pas nulle (résistance au cisaillement de la couche de corrosion), alors on peut réécrire :
|
|
|
où Ψ peut être identifié comme le rapport volumique de turbidité stockée. Si, au moins initialement, φ ne prend que les valeurs 0 ou 1, et est égal à 1 sur tout l’intervalle d’intégration, alors on peut réécrire :
|
|
|
L’équation de la résistance au cisaillement de la couche de corrosion en fonction du rapport volumique de turbidité stockée est donc la suivante :
|
|
|
Seuls deux paramètres sont requis en entrée : θmax, la résistance maximale au cisaillement, et une valeur initiale pour θC, la résistance initiale au cisaillement.
Dans une modification de l’article de Furnass et al (2014), l’érosion est notée :
|
|
où : θa est la contrainte de cisaillement appliquée à la paroi à l’instant t. |
Si on l’intègre sur θ de θC à θa, on obtient :
|
|
|
Pour InfoWorks WS, cela a été réécrit :
|
|
|
avec l’exposant 2 généralisé à n. Le paramètre γe, le coefficient d’érosion, a pour unité s-1 et, avec une valeur pour n, l’exposant d’érosion, est requis en entrée.
Furnass et al. (2014) donne une expression pour le taux de libération de matière d’une unité de surface de paroi de canalisation qui, après intégration sur θ, a été réécrite :
|
|
|
Le coefficient de libération λ a pour unité NTU.m et est requis en entrée.
Le changement de turbidité ΔT dû à l’érosion dans le temps Δt est donc obtenu en multipliant par la surface balayée, As, et en divisant par le volume dans lequel la matière est libérée, QΔt, ou, en utilisant :
|
|
|
on obtient :
|
|
|