Material Stress Dependence
Description: Specifies stress-dependent material properties for use in nonlinear analysis. This entry is used if a MAT1, MAT2, MAT8, MAT9, or MAT12 entry is specified with the same MID.
Format:

Example:

| Field | Definition | Type | Default | ||||
|---|---|---|---|---|---|---|---|
| MID | Identification number of a MAT1, MAT2, MAT8, MAT9, or MAT12 entry. | Integer > 0 | Required | ||||
| TID | Identification number of a TABLES1 or TABLEST entry. If H is given, then this field must be blank. See Remark 3. | Integer ≥ 0 or blank | |||||
| TYPE | Type of material nonlinearity, one of the following character variables: NLELAST for nonlinear elastic or PLASTIC for elastic-plastic. See Remarks. | Character | Required | ||||
| H | Work hardening slope (slope of stress vs. plastic strain) in units of stress. For more than a single slope in the plastic range, the stress-strain data must be supplied on a TABLES1 entry referenced by TID, and this field must be blank. See Remark 2. | Real | |||||
| YF | Yield function criterion, selected by one of the following values:
|
Integer | von Mises | ||||
| HR | Hardening rule, selected by one of the following values:
|
Integer | Isotropic | ||||
| LIMIT1 | Initial yield point. Y 1 for von Mises and Tresca yield criteria and 2 * Cohesion, 2c (in units of stress). | Real | 0.0 | ||||
| LIMIT2 | Internal friction angle (measured in degrees) for the Mohr-Coulomb and Drucker-Prager yield criteria. | Real | 0.0 |
Remarks:
- If TYPE = NLELAST, then MID may refer to a
MAT1 entry only. The TID in field three must be specified. The stress-strain data given in the
TABLES1 entry will be used to determine the stress for a given value of strain. If specified, the values H, YF, and LIMIT will be ignored in this case.
Thermoelastic analysis with temperature-dependent material properties is available for linear and nonlinear elastic isotropic materials (TYPE = NLELAST) and linear elastic orthotropic and anisotropic materials. Four options of constitutive relations exist. The relations appear in the table below along with the required Bulk Data entries.
Constitutive Relation Require Bulk Data Entries 
MATi and MATTi where i =1, 2, 8, or 9 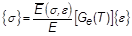
MAT1, MATT1, MATS1, and TABLES1 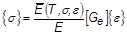
MAT1, MATS1, TABLEST, and TABLES1 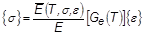
MAT1, MATT1, MATS1, TABLEST, and TABLES1 In Table 1,
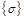 and
and
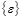 are the stress and strain vectors,
are the stress and strain vectors,
 the elasticity matrix,
the elasticity matrix,
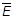 the effective elasticity modulus, and
the effective elasticity modulus, and
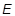 the reference elasticity modulus.
the reference elasticity modulus.
- If TYPE = PLASTIC, either the table identification TID or the work hardening slope H may be specified, but not both. If the TID is omitted, the work hardening slope H must be specified unless the material is perfectly plastic. The plasticity modulus (
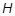 ) is related to the tangential modulus (
) is related to the tangential modulus (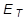 ) by:
) by:

where
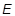 is the elastic modulus and
is the elastic modulus and
 is the slope of the uniaxial stress-strain curve in the plastic region. See Figure 1.
is the slope of the uniaxial stress-strain curve in the plastic region. See Figure 1.
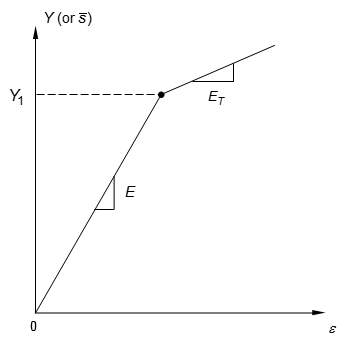
Figure 1. Stress-Strain Curve Definition When H is Specified in Field 5
- If TID is given,
TABLES1 entries (Xi, Yi) of stress-strain data (
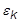 ,
,
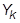 ) must conform to the following rules (see Figure 2):
) must conform to the following rules (see Figure 2):
- If TYPE = PLASTIC, the curve must be defined in the first quadrant. The first point must be at origin (X1 = 0, Y1 = 0) and the second point (X2, Y2) must be at the initial yield point (
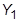 or
or
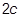 ) specified on the MATS1 entry. The slope of the line joining the origin to the yield stress must be equal to the valued of
) specified on the MATS1 entry. The slope of the line joining the origin to the yield stress must be equal to the valued of
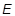 . Also, TID may not reference a
TABLEST entry.
. Also, TID may not reference a
TABLEST entry.
- If TYPE = NLELAST, the full stress-stress curve (-∞ < x < ∞) may be defined in the first and the third quadrant to accommodate different uniaxial compression data. If the curve is defined only in the first quadrant, then the curve must start at the origin (X1 = 0.0, Y1 = 0.0) and the compression properties will be assumed identical to tension properties.
- If TYPE = PLASTIC, the curve must be defined in the first quadrant. The first point must be at origin (X1 = 0, Y1 = 0) and the second point (X2, Y2) must be at the initial yield point (
- Material nonlinear behavior requires a nonlinear solution.
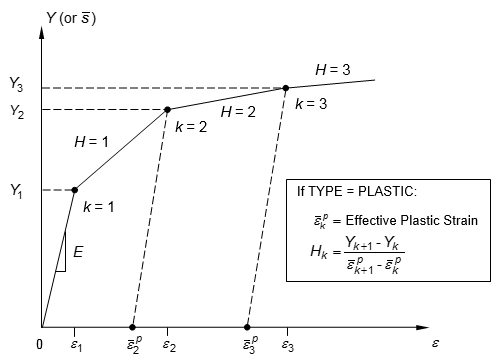
Figure 2. Stress-Strain Curve Definition When TID is Specified in Field 3