网格

有限元方法通过将真实物体分解为大量（1,000 到 100,000 个）元素（如小四面体或立方体，称为“网格”）来进行分析。通过设置数学方程式预测每个元素的行为。计算机将结合所有单个元素行为来预测整个零件或部件的行为。

曲面网格的质量和实体元素的形状可显著影响仿真结果的准确性。此外，网格密度（即，单位体积的单元数）也将影响结果的准确性。请注意网格的质量和局部网格细化，以通过网格收敛技术最大限度地提高结果的准确性。

Autodesk Fusion 提供了自动网格生成功能，以及有关网格大小、网格质量、元素顺序和其他选项的全局和局部设置。

• 网格设置将应用于所有零部件。
• 局部网格控制应用于选定的实体。
• 每个仿真分析都具有自己的网格设置。

好的网格会在精度和计算时间之间取得平衡。高质量的网格可快速收敛，生成精确的结果，并且不会产生错误。大多数网格划分过程都包括指定适当的网格设置。

节点和元素

在对 Fusion 分析进行求解之前，几何图元将被分解为一些小块，这些小块称为元素。每个元素的角是一个节点。计算就在节点处执行。此外，可以在元素边的中点处包含节点。这些元素和节点构成网格。

求解的准确性取决于良好的网格，Fusion 可以自动化完成大部分网格创建过程，从而帮助您为仿真创建良好的网格。

节点是定义了自由度 (DOF) 的空间中的坐标位置。对于结构分析，自由度表示由于结构载荷的作用点发生的可能移动。材料的应变由节点的相对运动来确定，而应力是根据应变和材料特性计算的。对于热分析，唯一的自由度是每个节点处的温度。然后，根据温度分布和材料的热导率来确定热通量。自由度还会影响从一个元素传递到下一个元素的力和力矩。系统将提供节点处有限元分析的结果（变形、应力、温度、热通量率）。

在现实世界中，点可以在六个不同的方向上移动：在 X、Y 和 Z 轴方向上平动，以及绕 X、Y 和 Z 轴转动。在有限元分析中，节点在经过计算的运动中可能会由于种种原因受到限制。例如，不需要对二维元素计算平面外平动。如果二维元素的节点移出平面外，那么它就不是二维元素。此外，对于实体元素，不会考虑节点转动。实体元素中的所有变形仅是节点平动的结果。但是，平面和直线元素通常支持转动自由度。

节点的自由度与通过节点传递到元素的力、约束或热流量的类型有关。轴向力或剪切力与平动自由度相对应，因为元素的刚度可确定当节点承受特定载荷作用时移动的距离。力矩与转动自由度相对应。因此，若要传递围绕特定轴的力矩，节点必须具有围绕该轴的转动自由度。如果节点没有转动自由度，则向该节点应用力矩对分析没有影响。同样，如果节点不能传递力矩，那么使用转动边界条件约束该节点也不会有任何作用。

元素是有限元分析的基本组成部分。有不同的元素类型，并且其使用取决于模型和分析类型。当前，Fusion 中的所有实体元素均为四面体（每个包含四个三角面和六条边）。线性四面体元素具有四个节点。抛物线四面体元素沿每条边添加一个中部节点，从而使每个元素共有十个节点。抛物线四面体元素有两种变体：包含弯曲边和不包含弯曲边。

表 1：四面体元素变体。

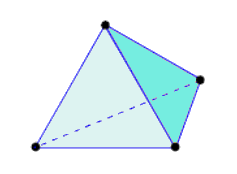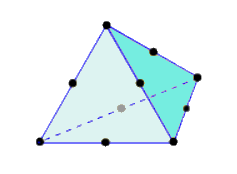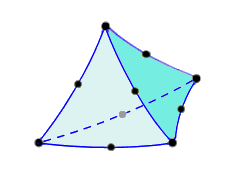线性四面体	抛物线四面体	包含弯曲边的抛物线四面体
（4 个节点）	（10 个节点）	（10 个节点）

元素是一种用于定义一个节点的自由度与下一个节点之间关联方式的数学关系。此数学关系还定义了变形创建应力的方式。