Modal frequencies study

All things vibrate, and we are all familiar with many sources of vibration, such as:

• Musical instruments
• Riding in a car with tires that are out of balance
• Rattles in an airplane when the pilot revs up the engines
• The vibration under your feet when a train passes

Prolonged vibration is detrimental to structures, vehicles, and other types of machinery. It is also frequently unavoidable. Unchecked, vibration can lead to eventual metal fatigue and part or structure failure. Vibration is about frequencies. By its very nature, vibration involves repetitive motion. Each occurrence of a complete motion sequence is called a cycle. Frequency is defined as so many cycles in a given time period. One cycle per second is equivalent to 1 Hertz.

The natural frequencies of a structure are affected by tensile or compressive stresses resulting from applied loads. For this reason, Autodesk Fusion includes an option to Compute Preloaded Modes. The effects of applied modes are ignored when this option is not activated.

What are Modal Frequencies?

Structures exhibit multiple natural frequencies of vibration when excited by an imposed force, acceleration, or displacement. The way that the structure moves for a particular natural frequency is referred to as the mode shape. Mode shapes might involve bending, twisting, elongation and contraction, or a combination of these effects. There are several types on modal frequencies, as follows:

• Rigid body modes: Oscillatory movement (specifically translation) in the global directions or rotation about the global axes. These modes can only occur when the model is unconstrained in one or more directions. The model does not deform, it just moves relative to its original location. Sometimes, a constraint prevents the structure from vibrating in every possible mode shape. Therefore, it can be useful to run a modal analysis on an unconstrained model, though the rigid-body modes are usually not meaningful.

• Fundamental modes: The first (lowest frequency) mode (excluding rigid-body modes). For example, the shape of a diving board when someone is standing on the outboard end is similar to the first fundamental vibration mode:

  

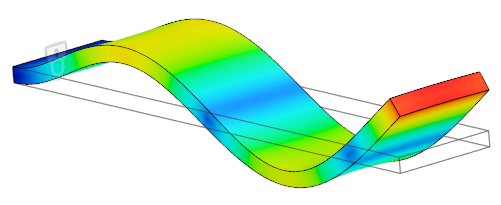
• Harmonic modes: Typically, a multiple of one of the fundamental modes. Harmonic mode shapes are more complex than fundamental modes and have more points of inflection. Going back to our diving board example, here is an image of the second harmonic of the fundamental vibration mode. There are two points of inflection along the length (dark blue), not counting the anchored end of the board:

  

There can be a simple up and down motion for one mode. Then, a simple side to side or front to back motion may occur at a higher frequency. In between these simple fundamental modes, we may discover one or more harmonic vibrating modes. Therefore, the shape does not necessarily become more complex for each successive (higher-frequency) mode. However, the overall trend is for the shapes to become more complex as the vibrating frequency increases.

The following factors influence the natural frequencies and mode shapes:

• The shape of the structure
• The mass of the structure and how that mass is distributed
• The way the structure is constrained
• The stiffness of the material and structure
• The tensile or compressive loads applied to the structure

Consider a piano, guitar, or violin string. The greater the mass of the string, the lower its vibrating frequency. Conversely, the greater the string tension, the higher its vibrating frequency. The strongest vibration is the first fundamental mode (or base frequency), in which the whole string moves back and forth in a simple arc shape. The string shape becomes an S-curve for the first harmonic mode. That is, there is one point of inflection midlength, and the half-string portions move in opposite directions. Overtones occur when a higher frequency vibration is superimposed over a lower frequency mode.

Why perform a Modal Frequencies analysis?

Severe consequences can occur when a power source, such as a motor, produces a frequency at which an attached structure naturally vibrates. When something is excited at a natural frequency, the vibration is amplified. This phenomenon is called resonance. When vibration causes resonance in an object, destruction can occur, unless the parts are designed to withstand the stress.

Engineers must design so that resonance does not occur during regular operation of machines. It is a major purpose of modal frequencies analysis. Ideally, the first mode has a frequency higher than any potential driving frequency. Alternatively, the driving frequencies at operating speeds may exceed the natural frequency. In this case, the design must withstand the momentary resonance that occurs while the machine is accelerating to the operating speed.

For certain special cases, the engineer may want a design to resonate. An ultrasonic cleaner is an example of such a device. To minimize the power required to vibrate the machine, and to maximize the vibration magnitude, excite the structure at its natural frequency.

Whether your goal is to avoid or target natural frequencies, a Modal Frequencies simulation is a crucial part of the design process.