El procedimiento de Laurenson se puede aplicar a cuencas vertientes rurales y urbanas en situaciones de simulación continua y de aguas pluviales de diseño. Permite la respuesta no lineal de cuencas en una amplia variedad de magnitudes de eventos.
El procedimiento Laurenson también se conoce como método RAFTS, y es originario de un estudio de Aitken, A.P. (1975). Sin embargo, esta ecuación se repite en: ARR, volumen 1, en la página 187. Véase también la referencia Sobinoff et.al. (1983). La ecuación solo es adecuada para un valor n de 0,025.
Willing y sus socios realizaron más modificaciones tras las ejecuciones de calibración en cuencas del proyecto entre 1976 y 1985.
Los requisitos de datos hidrológicos son los siguientes: cuenca vertiente, talud, grado de urbanización, tasas de pérdida, lluvia observada o lluvia de diseño.
Estos datos se utilizan para calcular el coeficiente de retardo de almacenamiento para cada una de las subcuencas vertientes y, por tanto, para desarrollar el hidrograma de escorrentía no lineal. Se adopta un exponente por defecto, aunque el usuario puede modificar este valor con un exponente no lineal diferente o con una tabla de calificación de caudal frente a un exponente para definir diferentes grados de respuesta no lineal de cuenca vertiente.
En las secciones siguientes se proporciona más información sobre las distintas ecuaciones utilizadas.
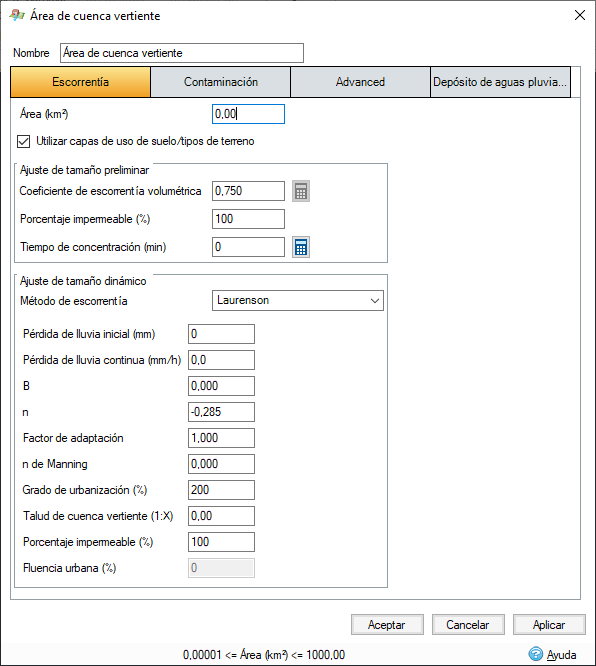
Pérdida de lluvia inicial: especifica la profundidad de lluvia que se infiltra antes de que se produzca cualquier escorrentía.
Pérdida de lluvia continua: especifica la pérdida que se produce una vez terminada la pérdida inicial.
B: se puede introducir o calcular a partir de la ecuación de la sección "Coeficientes B y n" que aparece a continuación.
n: el exponente de no linealidad de almacenamiento se establece por defecto en -0,285
Factor de adaptación: se puede utilizar como factor de multiplicación utilizado durante la calibración para modificar el valor de B calculado. El valor por defecto será 1.
N de Manning: PERN es un factor de adaptación que se utiliza para introducir el efecto de la rugosidad de cuencas vertientes permeables, como se indica a continuación:
|
n |
PERN |
|---|---|
|
0,010 |
0,4 |
|
0,015 |
0,5 |
|
0,025 |
1,0 |
|
0,100 |
3,0 |
Grado de urbanización: fracción de cuenca vertiente urbanizada.
Talud de cuenca vertiente: talud de área igual modificado (%).
Porcentaje impermeable: parte impermeable del área Caudal de entrada.
Fluencia urbana: ajusta la escala del área impermeable según la cantidad especificada. Esto se puede utilizar para tener en cuenta el aumento de las zonas urbanas u otros factores. Este valor solo se activa (y se utiliza) cuando la fluencia de análisis de Criterios de análisis se establece en "Usar áreas de cuenca vertiente".
Relación de descarga-almacenamiento
Cada subárea se trata como un almacenamiento conceptual concentrado. Cada almacenamiento tiene un tiempo de retardo de almacenamiento descrito de esta manera:
K(q) = Bqn
donde:
K(q) = tiempo de retardo de almacenamiento de subárea (horas) como una función de q
q = descarga (m3/s)
B = coeficiente de retardo de almacenamiento
n = exponente de no linealidad de almacenamiento
La sustitución de la ecuación de almacenamiento no lineal en cascada en la ecuación de tiempo de retardo de almacenamiento proporciona:
s = Bqn + 1
donde:
s = volumen de almacenamiento (horas x m3/s)
B = coeficiente de retardo de almacenamiento
n = exponente de no linealidad de almacenamiento. Por defecto se establece en -0,285
La lluvia se aplica a cada subárea, se calcula un exceso y el exceso se convierte en un caudal de entrada instantáneo. Este caudal instantáneo se enruta a través del almacenamiento de subárea para desarrollar un hidrograma de salida de subcuenca vertiente individual.
El valor por defecto del exponente de no linealidad es -0,285. La aplicación proporciona los mecanismos para modificar este valor, normalmente en relación con los eventos poco frecuentes que implican un enrutamiento de crecidas de subcuenca vertiente significativo, mediante:
- Introducir directamente un valor modificado de «n». Un valor de cero indicaría la respuesta lineal de cuenca vertiente y se igualaría con la teoría hidrográfica de unidades.
- Introducir una curva de clasificación «n» = f (Q) para cada subcuenca vertiente.
De esta forma, la aplicación puede simular una respuesta lineal o no lineal.
Coeficientes B y n
B es una entrada directa para cada subcuenca vertiente o se calcula a partir de la ecuación siguiente, que fue derivada por Aitken (1975). Se supone que el valor de B para cada subárea es igual al valor medio de B para la subcuenca vertiente.
BAV = 0,285 A0.52 (1 + U)-1.97 Sc-0.50
donde:
B = valor medio del coeficiente B para la subcuenca vertiente
A = área de subcuenca vertiente (km²)
U = fracción de cuenca vertiente urbanizada. (Donde U = 1.0, la cuenca vertiente está totalmente urbanizada y cuando U = 0.0, la cuenca vertiente es completamente rural)
Sc = talud de desagüe principal de la subcuenca vertiente (%). (La ruta más larga de la subcuenca vertiente, empezando en la salida de la subcuenca vertiente que va por el canal principal, y después, si es necesario, se ramifica en el afluente más lejano, hasta la parte superior de la subcuenca vertiente.)
Esta ecuación se derivó inicialmente de seis cuencas vertientes urbanas en Australia, con los siguientes rangos:
A osciló entre 0,8 km² y 56 km²
U varió de 0.0 a 1.00
Sc varió del 0,22% al 2,90%.
Sin embargo, en los años siguientes se ha probado con gran éxito una amplia gama de áreas, taludes y urbanización fuera de estos intervalos. Véase Sobinoff et al. (1983).
Para cuencas vertientes con indicadores, los valores B deducidos, evaluados como el valor medio de los eventos de precipitación/escorrentía registrados, deben utilizarse en lugar de las estimaciones de regresión generalizadas.
Como U en algunos casos puede ser bastante impreciso, la introducción de datos a este respecto se ha modificado para incluir un parámetro % impermeable (%I) para cada subcuenca vertiente en lugar del término U.
El modelo interpreta U en términos de %I en función de las siguientes relaciones:
| %I | U |
|---|---|
| 0 | 0 |
| 30 | 0,7 |
| 50 | 1,0 |
| 100 | 2,0* |
* Este valor se extrapola de los datos originales en función de los resultados limitados de áreas totalmente impermeables.
Factores de modificación de B
Si hay datos de lluvia/escorrentía calificados disponibles para un intervalo de eventos, se deben utilizar en lugar de la ecuación de regresión anterior con factores de modificación.
PERN
La ecuación de regresión original (expresada en la sección «Coeficientes B y n») no distingue entre cuencas vertientes con el mismo grado de urbanización, pero con una aspereza diferente. Por lo tanto, se ha añadido un parámetro empírico adicional para tener en cuenta la rugosidad de subcuenca vertiente permeable.
El parámetro PERN se introduce como una representación «n» de Manning de la rugosidad media de la subcuenca vertiente. B se modifica de acuerdo con la siguiente tabla. Si PERN se deja en blanco, B no se modifica.
|
n |
PERN |
|---|---|
| 0,010 | 0,4 |
| 0,015 | 0,5 |
| 0,025 | 1,0 |
| 0,100 | 3,0 |
Es habitual que un análisis de subcuenca vertiente dividida calcule un valor máximo de subcuenca vertiente inferior que un valor máximo utilizando solo una definición de subcuenca vertiente (componente impermeable y permeable).
En función de un estudio que calibra cuencas vertientes urbanas en Canberra, los parámetros de enrutamiento de escorrentía de superficie para la rugosidad de PERN Manning para las áreas impermeables y permeables son 0,015 y 0,040 respectivamente. (Willing y socios, 1993)
BX
Durante la calibración de una cuenca vertiente con indicadores, se incluye un parámetro adicional BX en los datos de encabezamiento para modificar el valor calculado o la entrada B mediante un factor de multiplicación adicional. El parámetro BX modificará de forma uniforme todos los valores de la subcuenca vertiente B calculados previamente, o bien se definirá en la ecuación expresada en la sección «Coeficientes B y n».
Método de enrutamiento
El enrutamiento de una subcuenca vertiente concreta se realiza mediante el método Muskingum-Cunge. El almacenamiento se considera una función no lineal de la descarga.
s = K(q) x q Ecuación (1)
donde:
s = volumen de almacenamiento (horas × m³/s)
q = velocidad instantánea de escorrentía (m³/s)
K(q) = tiempo de retardo de almacenamiento como una función de q (horas)
La función de almacenamiento se utiliza en la ecuación de continuidad en forma de diferencia finita:
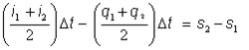Ecuación (2)
donde:
i1, i2 = Afluencia al inicio y al final del período de enrutamiento (m³/s)
delta t = intervalo de enrutamiento (horas)
q1, q2 = descarga del almacenamiento al principio y al final del período de enrutamiento (m³/s)
s1, s2 = volumen de almacenamiento al principio y al final del período de enrutamiento (horas × m³/s)
Al sustituir 2 y s 1 en Ecuación (2) desde Ecuación (1) se obtiene:
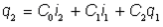
donde:
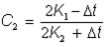
Se requiere una solución iterativa debido a la interrelación entre C0, C1, C2, K2 y q2. K1 y K2 son los tiempos de retardo de almacenamiento de subáreas calculados como una función de q al principio y al final de la iteración respectivamente.
Detalles de ruta
El procedimiento de enrutamiento de grupos de nivel de polo se utiliza en el módulo de la cuenca de retardo. El hidrograma de caudal de entrada se enruta a través de la cuenca mediante el enrutamiento de almacenamiento que se describe a continuación:
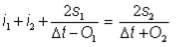
donde:
i1, i2 = caudales de entrada en los tiempos 1 y 2 (m³/s)
s1, s2 = almacenamiento total en los tiempos 1 y 2 (m³)
O1, O2 = desemboca en tiempos 1 y 2 (m³/s)
delta t = intervalo(s) de enrutamiento
Los subíndices 1 y 2 hacen referencia al comienzo y al final del intervalo de enrutamiento respectivamente.
Referencias
Aitken, A.P. (1975), Hydrologic investigation and design of urban stormwater drainage systems (Investigación hidrológica y diseño de sistemas urbanos de drenaje de aguas pluviales). Aust. Water Resources Council Tech. Documento n.º 10, Dept of the Environment and Conservation, A.G.P.S., Canberra.
Institution of Engineers, Australia. (1987) Australian Rainfall and Runoff - A Guide to Flood Estimation (editada por D.H. Pilgrim y R.P. Canterford), volúmenes 1 y 2, edición revisada, noviembre de 1987, Canberra
James 1998, editor Modeling the Management of Stormwater Impacts (Modelización de la gestión del impacto de las aguas pluviales), volumen 6, capítulo 23, autores: Ashok Pandit y Joanie Regan, What is the Impervious Area Curve Number. Editorial CHI Guelph, Ontario (Canadá).
Laurenson E.M. (1964) A Catchment Storage Model for Runoff Routing (Un modelo de almacenamiento de cuencas vertientes para enrutamiento de escorrentías), Journal of Hydrology, volumen 2, p. 141-163
Sobinoff, P. Pola, J.P. and O’Loughlin, G.C. (1983) Runoff routing parameters for the Newcastle-Sydney-Wollongong region (Parámetros de enrutamiento de escorrentía para la región de Newcastle-Sydney-Wollongong). Hydrol. And Water Resources Symposium 1983, inst. Engrs Aust., Natl Conf. publ. N.º 83/13, páginas 28-32. T
USDA National Resources Conservation Service, 1986, Urban Hydrology for Small Watersheds (Hidrología urbana para pequeñas cuencas hidrográficas), Technical Release 55.
Viessman W. et al 1977, Introduction to Hydrology (Introducción a la hidrología), Harper &Row Publishers, Nueva York
WEF 1992, Manaual of Practice FD-20 Design and Construction of Urban Stromwater Management Systems (Diseño y construcción de sistemas urbanos de drenajes de aguas pluviales), ASCE y WEF ISBN 0-87262-855-8