Exercice 4 : Résoudre l’analyse et examiner les résultats

Dans une étude de Contrainte statique non linéaire, la solution est calculée sur plusieurs incréments. Dans ce didacticiel, la charge de pression sur la poutre est appliquée progressivement sur 60 pas, ce qui vous permet de voir l’effet de la charge sur le temps.

Dans cet exercice, vous :

• résolvez l’étude ;

• déterminez si la poutre est susceptible de se réduire ;

• identifiez quand le Facteur de sécurité descend en dessous de 1 ;

• examinez le résultat Contrainte de von Mises pour voir comment les contraintes changent au cours du chargement de la poutre de support ;

• examinez le résultat Déplacement pour identifier le moment où le déplacement commence à augmenter de manière exponentielle.

  

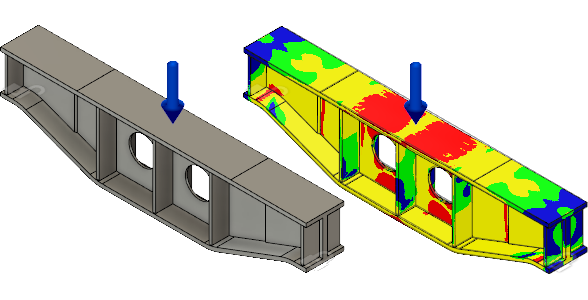
  Modèle de poutre de support avec des contraintes et des charges appliquées (à gauche) et le résultat de facteur de sécurité de contrainte statique non linéaire (à droite).

Conditions préalables

• L’exercice 3 est terminé.

Étapes

1. Résolvez l’étude.

   1. Cliquez sur (espace de travail Simulation > onglet Configurer > groupe de fonctions Résoudre > Résoudre) pour ouvrir la boîte de dialogue Résoudre.
      
      Remarque : l’icône de vérification préalable affiche une coche verte , qui indique qu’il n’y a pas d’avertissements et que le modèle est prêt à être résolu.
   2. Sélectionnez l’étude à résoudre.
   3. Cliquez sur Résoudre 1 étude pour exécuter l’analyse et fermer la boîte de dialogue.

      Remarque : le maillage et la résolution de l’analyse peuvent prendre plusieurs minutes.

   4. Lorsque l’analyse est terminée, cliquez sur Fermer pour fermer la boîte de dialogue État de la tâche.

      L’onglet Résultats s’ouvre automatiquement, ce qui vous permet de visualiser les résultats.

2. Affichez les résultats du Facteur de sécurité et déterminez si la poutre est susceptible de se réduire sous la charge appliquée.

   1. Le résultat Facteur de sécurité à l’étape 60 s’affiche la première fois que la solution de l’étude est terminée. Toutefois, si vous réexécutez la solution, le résultat le plus récemment affiché est conservé à la fin. Si nécessaire, choisissez Facteur de sécurité dans la liste déroulante des résultats à proximité de la légende.
      
      
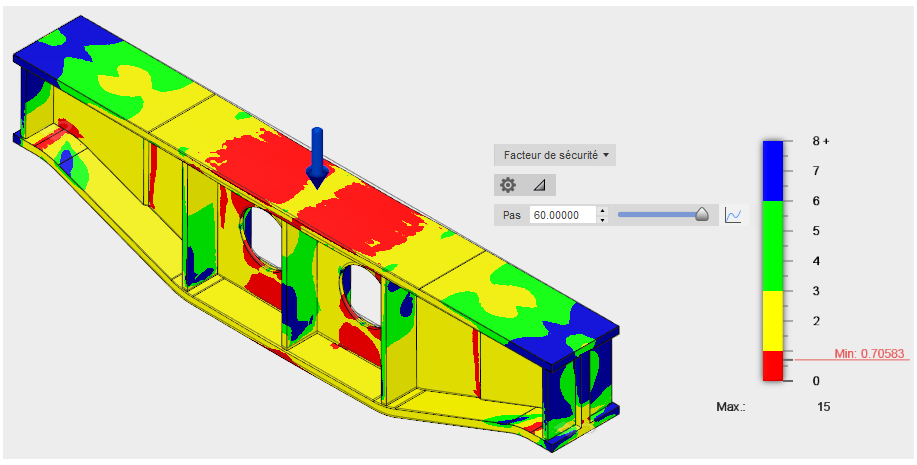
   2. Faites glisser le curseur d’avant en arrière pour voir comment le facteur de sécurité varie à mesure que la charge augmente. La charge s’élève de façon linéaire tout au long de la simulation à une vitesse de 5 kN par pas (5 kN * 60 pas = 300 kN).

      Remarque : le facteur de sécurité minimal est d’environ 0,7, ce qui indique que la limite d’élasticité de la matière a été largement dépassée. En outre, une grande partie de la pièce de contour est rouge. Par conséquent, une déformation permanente s’est sûrement produite et la poutre menace de s’effondrer sous la charge appliquée.

3. Utilisez le Tracé des résultats transitoires pour identifier quand le facteur de sécurité tombe en dessous de 1,0.

   1. Dans la zone de légende du tracé, cliquez sur Graphique 2D à droite du curseur Étape.

      Conseil : cliquez sur la barre de titre Tracé de résultats provisoires et faites-la glisser pour repositionner la fenêtre du tracé. Vous pouvez également cliquer sur le coin inférieur droit de la fenêtre et le faire glisser pour le redimensionner.

   2. Cliquez sur la ligne de la marque de temps et faites-la glisser sur le graphique pour localiser le point auquel le facteur de sécurité chute à 1.0.
      
      
      
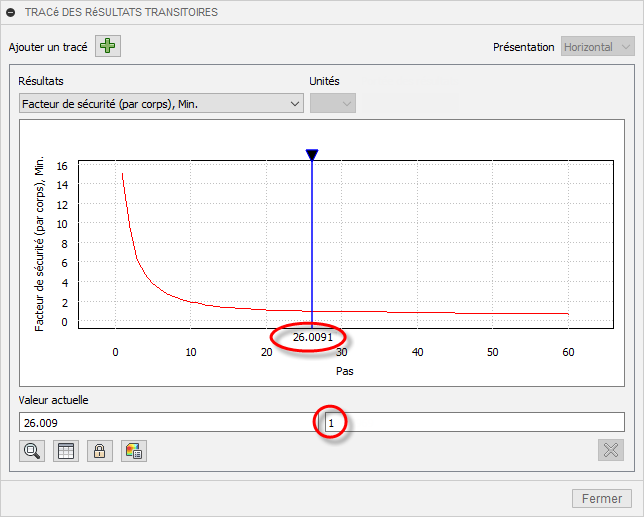
      Notez que le facteur de sécurité passe à 1.0 à la 26e étape du calcul environ. À partir de cette observation, nous pouvons conclure que la charge devient critique à environ 43 % de la charge appliquée, soit 130 kN :

      (Étape 26 / 60 = 0,433 et 0,433 * 300 kN = 130 kN)

   3. Cliquez sur Fermer pour ignorer le graphique.

4. Affichez le résultat de la contrainte de Von Mises pour voir comment les contraintes changent au cours du chargement de la poutre de support.

   1. Sélectionnez la Contrainte dans la liste déroulante. Le type de contrainte par défaut affiché est von Mises.
   2. Faites glisser le curseur d’étapes pour voir comment les contraintes changent au cours du chargement de la poutre de support.
      
      
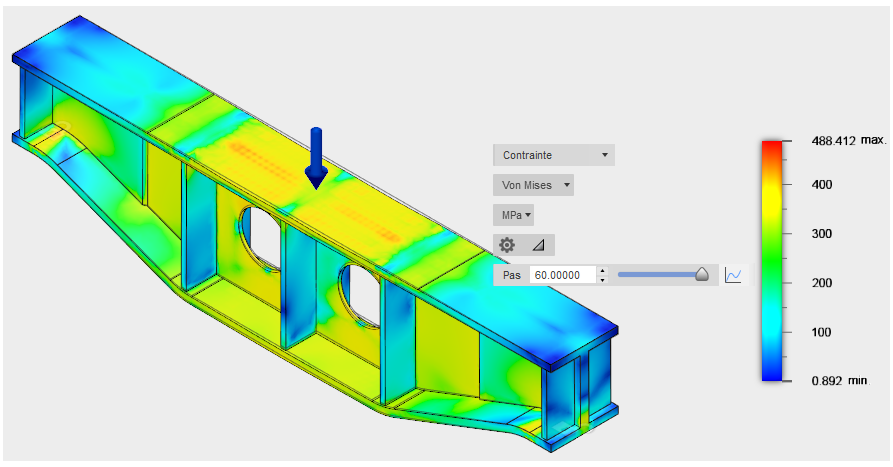
   3. Cliquez sur Tracé 2D pour afficher la contrainte maximale de von Mises tout au long de l’historique de charge.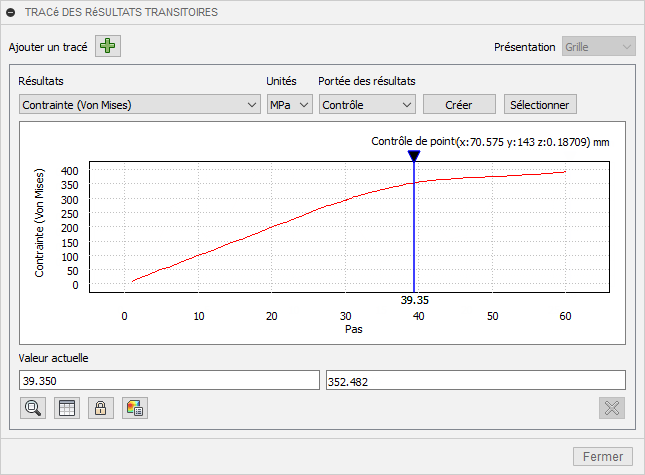
      
      
      
      Ici, le curseur est positionné pour indiquer le point au niveau duquel l’élasticité initiale commence, à environ 233,7 MPa pour cette matière.

      Notez la réponse non linéaire de la poutre. Plus la charge augmente, plus la poutre commence à être élastique. Une fois l'élasticité initiée, l'augmentation du taux de contrainte diminue. Au cours de ce processus, le matériau est en train de se durcir et de devenir de plus en plus fort. Si nous exécutons simplement une étude de contrainte statique linéaire sur la poutre, nous ne verrons que les contraintes sur la poutre à la fin de l'analyse. Les contraintes prévues seraient bien plus importantes, car la matière est supposée rester à sa rigidité élastique (module de Young).

      Conseil : si vous observez les propriétés de base de la matière, vous constatez que la limite d’élasticité est beaucoup plus grande que la contrainte d’élasticité initiale affichée sous les propriétés avancées (non linéaires). La raison en est que la contrainte d’élasticité de base est le point où la rigidité du matériau est décalée de 0,2 % par rapport au comportement linéaire. Ce décalage de 0,2 % est la base type des tensions nominales de la limite d'élasticité du matériau. La contrainte d'élasticité initiale non linéaire est le point où la rigidité commence à dévier du module de Young. Vous pouvez voir que la pente de la courbe de contrainte change plus rapidement une fois que la limite d’élasticité de base (environ 345 MPa) a été dépassée.

   4. Cliquez sur Fermer pour fermer le tracé 2D.

5. Affichez le résultat Déplacement pour identifier le moment où le déplacement commence à augmenter de manière exponentielle.

   1. Sélectionnez le résultat Déplacement dans la liste déroulante située à proximité de la légende.

      Le déplacement total est indiqué par défaut. Contrairement aux études linéaires, la forme déplacée réelle est affichée par défaut pour les études non linéaires. En d'autres termes, la distorsion n'est pas exagérée (vous pouvez toutefois choisir de le faire). Par conséquent, le déplacement semble moins élevé que ce que vous avez l'habitude de voir dans une analyse des contraintes statiques linéaires. Ne vous laissez pas tromper. Examinez les nombres de déplacement réels.

      
      
      
      
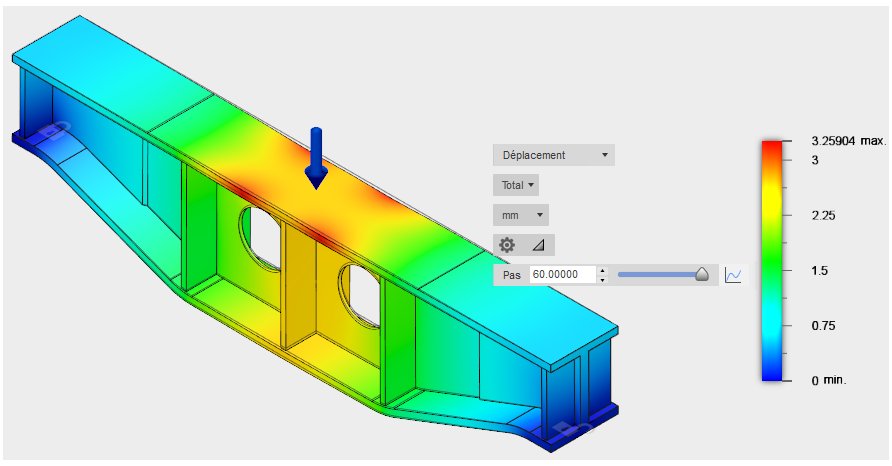
      Comme vous pouvez vous y attendre, le déplacement maximal se produit près de la travée médiane de la poutre et sur l’aile supérieure, où la charge est appliquée.
   2. Cliquez sur Tracé 2D pour afficher le Déplacement total maximum dans l’historique de charge.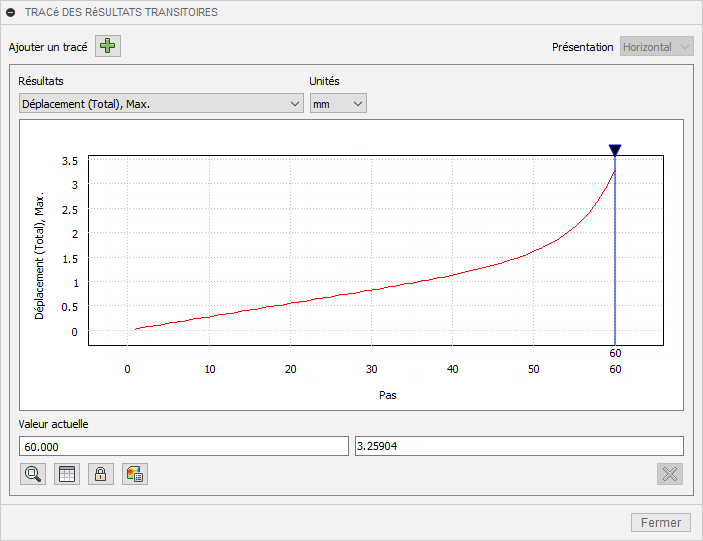
      
      
      
      Notez que le déplacement commence à augmenter de façon exponentielle à environ la 45e étape du calcul. À la fin de la simulation, la pente est assez raide. Les contraintes dépassant la limite d'élasticité se répartissent et pénètrent plus profondément, ce qui affecte une plus grande quantité de volume de poutre à mesure que l'étude progresse. Par conséquent, le matériau ne peut plus supporter la charge appliquée. Il est évident que la poutre est sur le point de s'effondrer.

Résumé de l'exercice 4

Dans cet exercice, vous avez :

• Résolu l’étude
• Déterminé si la poutre est susceptible de se réduire
• Identifié lorsque le Facteur de sécurité descend en dessous de 1
• Examiné le résultat de la Contrainte de von Mises pour voir comment les contraintes changent au cours du chargement de la poutre de support
• Examiné le résultat Déplacement pour identifier le moment où le déplacement commence à augmenter de manière exponentielle