La procédure de Laurenson peut être appliquée aux bassins versants ruraux et urbains dans les situations d’averse de projet et de simulation continue. Elle permet la réponse non linéaire des bassins versants sur une large gamme d’ampleurs d’événements.
La procédure de Laurenson, également connue sous le nom de modèle RAFTS, a été utilisée pour la première fois dans un document d’A.P Aitken (1975). L’équation sera ensuite reprise dans le document ARR Volume 1, à la page 187. Voir aussi la référence Sobinoff et al. (1983). L’équation est exclusivement réservée à une valeur n de 0,025.
D’autres modifications ont été apportées par Willing et Partners à la suite d’étalonnages réalisés sur les bassins versants de projet entre 1976 et 1985.
Les données hydrologiques obligatoires sont le bassin versant, la pente, le degré d’urbanisation, le taux de perte et la pluviométrie observée ou de projet.
Ces données servent à calculer le coefficient de retard de stockage pour chacun des sous-bassins versants et, par conséquent, à développer l’hydrogramme de ruissellement non linéaire. Un exposant par défaut est adopté, bien que vous puissiez remplacer cette valeur par un autre exposant non linéaire ou par un tableau de correspondance hauteurs-débit vs un exposant pour définir les différents degrés de réponse non linéaire des bassins versants.
Pour en savoir plus sur les différentes équations utilisées, reportez-vous aux sections ci-dessous.
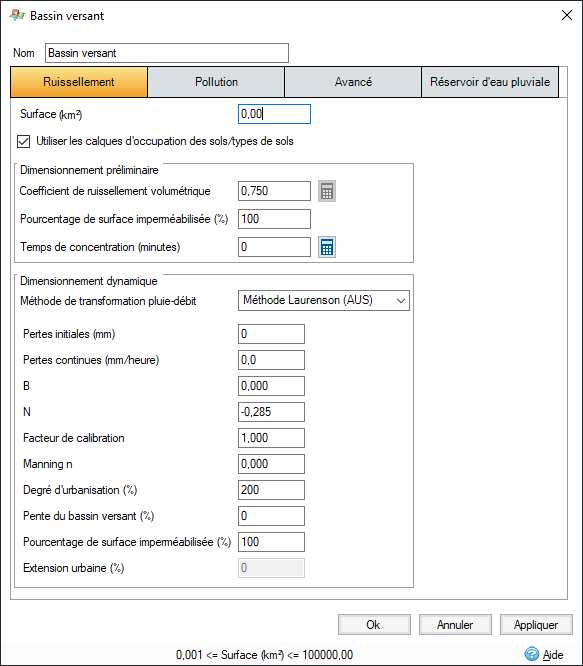
Perte initiale de pluviométrie : indique la hauteur de précipitation qui s’infiltre avant tout écoulement.
Perte continue de pluviométrie : indique la perte qui se produit après la perte initiale.
B - Vous pouvez saisir ou calculer cette valeur à partir de l’équation présentée dans la section « Coefficients B et n » ci-dessous.
n : l’exposant de non-linéarité de stockage par défaut est défini sur -0,285
Facteur d’adaptation : ce facteur peut être utilisé comme facteur de multiplication pendant l’étalonnage pour modifier le résultat B. Sa valeur par défaut est 1.
Coefficient de Manning n : PERN désigne un facteur d’adaptation utilisé pour introduire l’effet de rugosité d’un bassin perméable comme suit :
|
n |
PERN |
|---|---|
|
0,010 |
0,4 |
|
0,015 |
0,5 |
|
0,025 |
1,0 |
|
0,100 |
3,0 |
Degré d’urbanisation : fraction de bassin versant en zone urbanisée.
Pente du bassin versant : pente de la surface égale modifiée (%).
Pourcentage d’imperméabilité : portion de surface imperméable de la zone d’apport.
Extension urbaine : cette option met à l’échelle la surface imperméable à l’aide de la valeur spécifiée. Elle peut être utilisée pour prendre en compte l’augmentation des zones urbaines, ou d’autres facteurs. Elle est uniquement activée (et utilisée) lorsque le fluage des critères d’analyse est défini sur « Utiliser les valeurs de bassin versant ».
Relation stockage-vidange
Chaque sous-surface est traitée comme un stockage conceptuel concentré. Chaque stockage a un délai de stockage décrit ainsi :
K(q) = Bqn
où :
K(q) = délai de stockage de sous-surface (heures) en fonction de q
q = vidange (m3/s)
B = coefficient de temps de retard de stockage
n = exposant de non-linéarité de stockage
Le remplacement de l’équation de stockage non linéaire en cascade par l’équation de délai de stockage permet d’obtenir le résultat suivant :
s = Bqn + 1
où :
s = volume de stockage (h x m3/s)
B = coefficient de temps de retard de stockage
n= exposant de non-linéarité de stockage. Par défaut, cette valeur est définie sur -0,285
La pluviométrie est appliquée à chaque sous-surface, la pluie excédentaire est calculée et l’excédent est converti en afflux instantané. Ce débit instantané est ensuite propagé à travers le stockage de sous-surface pour concevoir un hydrogramme d’exutoire de sous-bassins versants individuel.
La valeur par défaut de l’exposant de non-linéarité est -0,285. L’application fournit les mécanismes permettant de modifier cette valeur, généralement en cas d’événements rares impliquant un routage de débordement de sous-bassin versant important, en :
- Saisissant directement la valeur modifiée « n ». Une valeur de zéro indique une réponse linéaire du bassin versant et équivaut à la théorie de l’hydrogramme unitaire.
- Entrez une courbe de classification « n » = f (Q) pour chaque sous-bassin versant.
De cette manière, l’application peut simuler une réponse linéaire ou non linéaire.
Coefficients B et n
B est soit directement saisi pour chaque sous-bassin versant, soit estimé à partir de l’équation ci-dessous, qui a été calculée par Aitken (1975). La valeur de B pour chaque sous-surface est supposée être égale à la valeur moyenne de B pour le sous-bassin versant.
BAV = 0,285 A0.52 (1 + U)-1.97 Sc-0.50
où :
B = valeur moyenne du coefficient B pour le sous-bassin versant
A = zone de sous-bassin versant (km²)
U = fraction urbanisée du bassin versant. (où U = 1.0, le bassin versant est complètement urbanisé et où U = 0.0, le bassin versant est complètement rural)
Sc = talus de drainage principal du sous-bassin versant (%). (La trajectoire la plus longue du sous-bassin versant, qui commence à la sortie du sous-bassin versant remontant le canal principal, puis, si nécessaire, qui se ramifie au niveau de l’affluent le plus éloigné, jusqu’au sommet du sous-bassin versant.)
Cette équation a été initialement dérivée de six bassins versants urbains en Australie, avec les plages suivantes :
A variait de 0,8 km² à 56 km²
U variait de 0,0 à 1,00
Sc variait de 0,22 % à 2,90 %.
Cependant, au cours des années suivantes, un large éventail de zones, de pentes et de surfaces d’urbanisation en dehors de ces aires ont été testées avec un grand succès. Voir Sobinoff et al. (1983).
Pour les bassins versants mesurés, les valeurs B déduites, calculées comme la valeur moyenne des événements de pluie/ruissellement enregistrés, doivent être utilisées de préférence aux estimations de régression généralisées.
Comme U peut parfois être plutôt vague, les données entrées à cet égard ont été modifiées pour inclure un paramètre de % imperméable (%I) pour chaque sous-bassin au lieu de la condition U.
Le modèle interprète U en termes de %I selon les rapports suivants :
| %I | U |
|---|---|
| 0 | 0 |
| 30 | 0,7 |
| 50 | 1,0 |
| 100 | 2,0 |
* Cette valeur est extrapolée à partir des données d’origine en fonction de résultats limités provenant de zones complètement imperméables.
Coefficients de modification B :
Lorsque des données mesurées de pluviométrie/ruissellement sont disponibles pour une série d’événements, elles doivent être utilisées de préférence selon l’équation de régression ci-dessus avec les facteurs de modification.
PERN
L’équation de régression d’origine (exprimée dans la section « Coefficients B et n ») ne fait pas de différence entre les bassins versants présentant le même degré d’urbanisation mais une rugosité différente. Un paramètre empirique supplémentaire a donc été ajouté pour prendre en compte la rugosité du sous-bassin perméable.
Le paramètre PERN est entré en tant que représentation de la valeur « n » du coefficient de Manning correspondant à la rugosité moyenne du sous-bassin versant. B est ensuite modifié conformément au tableau suivant. Si PERN est laissé vide, B est inchangé.
|
n |
PERN |
|---|---|
| 0,010 | 0,4 |
| 0,015 | 0,5 |
| 0,025 | 1,0 |
| 0,100 | 3,0 |
Il est courant qu’une analyse de sous-bassin versant divisé évalue un pic de sous-bassin versant inférieur à un pic à l’aide d’une définition de sous-bassin versant groupé (composant imperméable plus perméable).
D’après une étude d’étalonnage de bassins versants urbains à Canberra, les paramètres de routage du ruissellement de surface pour la rugosité selon le paramètre Manning PERN pour les surfaces imperméables et perméables sont respectivement de 0,015 et 0,040. (Willing and Partners, 1993)
BX
Lors de l’étalonnage d’un bassin versant calibré, un facteur BX de paramètre supplémentaire dans les données d’en-tête est inclus pour modifier le paramètre calculé ou la valeur B d’entrée par un facteur de multiplication supplémentaire. Le paramètre BX modifie ensuite uniformément toutes les valeurs B de sous-bassin versant précédemment calculées ou définies dans l’équation exprimée dans la section « Coefficients B et n ».
Méthode de routage
Le routage d’un sous-bassin versant particulier est effectué à l’aide de la méthode de Muskingum-Cunge. Le stockage est considéré comme une fonction non linéaire de la vidange.
Équation s = K(q) x q (1)
où :
s = volume de stockage (h × m³/s)
q = taux instantané de ruissellement (m³/s)
K(q) = délai de stockage en fonction de q (heures)
La fonction de stockage est utilisée dans l’équation de continuité sous la forme de différences finies :
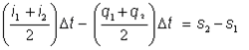Équation (2)
où :
i1, i2 = Afflux au début et à la fin de la période de routage (m³/s)
delta t = intervalle de routage (h)
q1, q2 = volume sortant du stockage au début et à la fin de la période de routage (m³/s)
s1, s2 = volume de stockage au début et à la fin de la période de routage (h × m³/s)
En substituant s2 et s1 dans l’équation (2) par rapport à l’équation (1), on obtient :
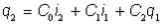
où :
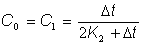
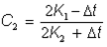
Une solution itérative est requise en raison de l’interrelation entre C0, C1, C2, K2 et q2. K1 et K2 correspondent aux temps de retard de stockage de sous-surface calculés en fonction de q au début et à la fin de l’itération, respectivement.
Détails du routage
La procédure de routage de bassin de Puls est utilisée dans le module de bassin de retenue. L’hydrogramme d’afflux est acheminé dans le bassin à l’aide de l’acheminement de stockage décrit ci-dessous :
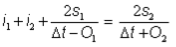
où :
i1, i2 = afflux aux moments 1 & 2 (m³/s)
s1, s2 = stockage total aux moments 1 & 2 (m³)
O1, O2 = volume sortant aux moments 1 & 2 (m³/s)
delta t = intervalle(s) de routage
Les indices 1 et 2 font respectivement référence au début et à la fin de l’intervalle de routage.
Références
Aitken, A.P. (1975) Hydrologic investigation and design of urban stormwater drainage systems. Technical paper (Australian Water Resources Council) n° 10, Dept of the Environment and Conservation, A.G.P.S., Canberra.
Institution of Engineers, Australia. (1987) Australian Rainfall and Runoff - A Guide to Flood Estimation (edited by D.H. Pilgrim and R.P. Canterford), Volumes 1 and 2, Revised Edition, November, 1987, Canberra
James 1998, Editor Modeling the Management of Stormwater Impacts Volume 6 Chapter 23 Author Ashok Pandit and Joanie Regan What is the Impervious Area Curve Number. Publisher CHI Guelph Ontario Canada.
Laurenson E.M. (1964) A Catchment Storage Model for Runoff Routing, Journal of Hydrology, Volume 2, pp 141-163
Sobinoff, P. Pola, J.P. et O’Loughlin, G.C. (1983) Runoff routing parameters for the Newcastle-Sydney-Wollongong region. Hydrol. And Water Resources Symposium 1983, inst. Engrs Aust., Natl Conf. publ. No. 83/13, pp. 28-32. T
USDA National Resources Conservation Service, 1986, Urban Hydrology for Small Watersheds, Technical Release 55.
Viessman W. et al 1977, Introduction to Hydrology", Harper&Row Publishers New York
WEF 1992, Manual of Practice FD-20 Design and Construction of Urban Stromwater Management Systems ASCE and WEF ISBN 0-87262-855-8