Terminal Velocity of a Falling Sphere

Analysis Characteristics

• Transient
• Free (unconstrained) Motion
• Gravity
• Buoyancy
• Turbulent
• Incompressible

Reference

Massey, Bernard Stanford, Mechanics of Fluids, 3rd Edition, Van Nostrand Reinhold Co, 1975, p. 347.

Problem Description

In this test model, a titanium sphere is dropped through a column of glycerin. The Motion capability is used to predict the terminal velocity of the sphere.

A falling object will reach a terminal velocity when the weight of the object is balanced by the buoyancy and drag forces due to the surrounding fluid:

W = Fb + D

W = the weight of the object

Fb = force due to buoyancy

D = drag force

For a sphere, the three quantities in the equation above are as follows:

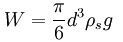
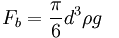
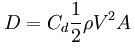
The resultant terminal velocity works out to be:

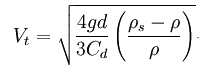
where:

• Vt = terminal velocity
• g = gravitational acceleration
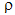• = fluid density
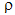• s = solid density
• A = 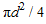= sphere projection area
• Cd = drag coefficient

Geometry and Boundary Conditions

All dimensions are in meters:

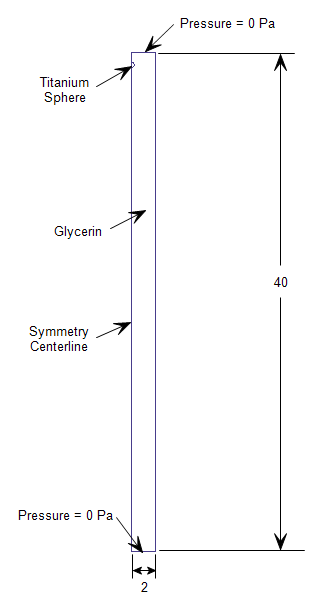
The model was solved as axisymmetric.

Results