Laminar Thermal-Driven Cavity

Analysis Characteristics

• Steady-state
• 2D internal flow
• Laminar
• Incompressible
• Natural convection

Reference

Davis, G. De Vahl and Jones, I.P., “Natural convection in a square cavity: a comparison exercise”, Inter. Jour. for Num. Meth. in Fluids, 3, (1983).

Problem Description

Temperature and velocity distributions are calculated for laminar, buoyancy-driven flow in a square cavity. The top and bottom walls are insulated, and the left and right walls are at fixed temperatures differing by 1 K.

The Rayleigh number is computed from:

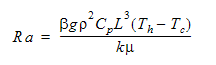
• is the coefficient of volumetric expansion, defined as:

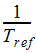
• g is the acceleration of gravity

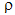• is the density

• is the specific heat

• L is the length of the cavity

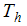• and 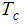are the temperatures of the left and right walls, respectively

• k is the conductivity of the fluid

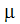• is the viscosity.

• Here, the Rayleigh number is 10,000.

This problem is analyzed to verify the fluid flow and heat transfer modeling capabilities of Autodesk® CFD. Accuracy is assessed by comparing velocity components at specific locations in the cavity. Velocities and coordinates are normalized in accordance with Davies, et al. (1983) as follows:

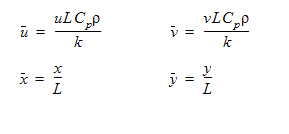
Geometry and Boundary Conditions

Results

Using the expressions defined above for 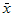, , 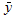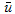and 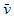, the following results are computed:

	Benchmark	2018: Build 20170308	% Error	2019: Build 20180130	% Error
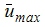	16.178	16.191	0.079	16.185	0.04399
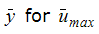	0.823	.825	.243	.825	.243
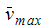	19.617	19.666	.251	19.651	.175
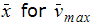	0.119	.120	.840	.120	.840