Un ingénieur allemand, nommé Albert, a mené les premières recherches connues sur la fatigue au début du XIXe siècle. Il avait compris qu'un matériau soumis à une charge répétée finissait par céder. Toutefois, c'est la défaillance généralisée et sans cause apparente des essieux de trains après un kilométrage élevé qui semble avoir attiré l'attention sur le phénomène connu aujourd'hui sous le nom de "fatigue".
La plupart des composants ou des structures d'un mécanisme sont soumis à une forme de charge cyclique. La défaillance de ces composants se traduit généralement par l'apparition de petites fissures, qui risquent de se transformer en fissures plus profondes et de provoquer un accident. Les premières fissures apparaissent à des niveaux de contrainte, bien en dessous de la contrainte d'élasticité monotone du matériau. Au fil du temps, les avaries (répétées) s'accumulent jusqu'à provoquer une éventuelle défaillance. Il est fréquemment avancé que 90 % des défaillances structurelles sont dues à des avaries liées à la fatigue.
Il existe principalement deux méthodes pour estimer le nombre de répétitions d'une charge cyclique qu'un matériau ou un composant est capable de supporter.
La première méthode utilisait les données de matériau rassemblées au XIXe siècle par Wholer. Cette technique associait la contrainte appliquée à un composant et une courbe empirique (connue comme courbe S-N ou courbe de Wholer) pour obtenir une estimation du nombre de cycles avant défaillance. Elle est toujours utilisée aujourd'hui et souvent appelée approche de longévité par contrainte. Cette technique, qui utilise la contrainte de composant, part du principe que la contrainte reste dans la zone élastique du matériau. Par conséquent, elle est plus adaptée aux défaillances de fatigue survenant après au moins 100 000 cycles.
La seconde méthode, plus moderne, prévoit les défaillances à partir de la déformation du matériau. Les courbes associant la déformation aux cycles peuvent être créées à partir de formules de test ou empiriques semblables à celles utilisées pour l'approche de longévité par contrainte. Le principal avantage de cette méthode est que la courbe de longévité par déformation représente l'état de déformation locale du composant et permet de prendre en compte une déformation plastique locale. Cela augmente considérablement la précision de la longévité estimée à des niveaux de charge où intervient l'élasticité locale.
L'assistant de fatigue utilise ces deux techniques afin de déterminer l'endurance.
Définition de charge
L'avarie de fatigue est causée par le chargement d'une structure avec des charges répétées sur une période donnée. Pour analyser la résistance à la fatigue, il faut définir la charge appliquée. Dans l'assistant de fatigue, vous pouvez définir deux types de charges, le plus simple étant une charge harmonique à amplitude constante.
Cette charge est décrite par la définition d'une amplitude de contrainte (sa) et d'une contrainte moyenne (sm). Le cycle répété est une période harmonique unique (points 1-2-3-4 dans la figure 1).
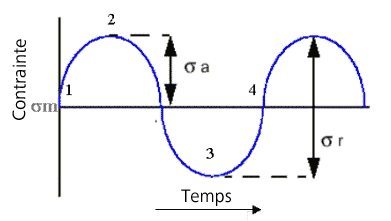
Figure 1 : Charge harmonique à amplitude constante
Le second type de charge, plus généralisé, est la charge à amplitude variable.
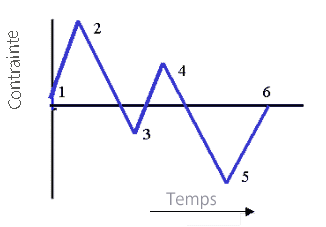
Figure 2 : Charge à amplitude variable
La charge à amplitude variable est constituée de nombreux cycles individuels à amplitude constante. Chacun de ces cycles peut avoir une amplitude et une moyenne différentes, et être superposé ou consécutif. La figure 2 présente un exemple simple de charge à amplitude variable. Vous pouvez observer la présence de deux cycles simples : 1-2-5-6 forme un même cycle de grande amplitude, dans lequel le cycle 3-4-3 est superposé. Une charge à amplitude variable peut être divisée en plusieurs petites charges à amplitude constante. Celles-ci sont alors utilisées dans l'analyse de fatigue pour prévoir une avarie.
Si le calcul de fatigue se base sur une charge à amplitude variable, il faut appliquer une méthode pour extraire les "sous-cycles". L'assistant de fatigue l'applique via un algorithme de comptage rainflow standard.
Comptage rainflow et avarie de fatigue
Les techniques de prédiction de fatigue basées sur la longévité par contrainte et par déformation reposent sur la courbe d'avarie d'un seul cycle. Cette courbe d'avarie associe le nombre de répétitions à l'amplitude des contraintes ou de la déformation au cours d'un seul cycle. Il est possible de l'utiliser directement dans le cas d'une charge structurelle simple à amplitude constante. Toutefois, si une charge à amplitude à variable est définie, il y a plusieurs étapes à suivre pour calculer la longévité en fonction de la charge appliquée.
L'historique de charge est en dents de scie. Ce processus analyse l'historique temporel de tous les points qui ne sont pas des "points d'inversion" et les ignore, ce qui réduit le volume de données inutiles. Ensuite, l'historique temporel réduit est traité par un algorithme de comptage rainflow standard qui extrait des cycles individuels. Ces cycles sont ensuite utilisés avec les courbes d'avarie de cycle unique afin de calculer une longévité pour chaque cycle.
Une fois la longévité calculée pour chaque cycle dans l'historique temporel, une méthode est requise pour déterminer l'avarie cumulée ou la longévité totale. L'assistant de fatigue utilise la règle de Miner, très bien documentée. Cette règle indique que le total des avaries cumulées tout au long de l'historique de charge est la somme linéaire des avaries des cycles individuels.
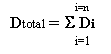
ou
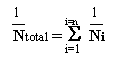
où N est la longévité dans les répétitions et D est l'avarie.
Technique de longévité par contrainte
La technique de longévité par contrainte utilise une courbe d'avarie à cycle unique, appelée courbe SN. Cette courbe associe l'amplitude de contrainte au nombre de cycles avant défaillance. Puisqu'il s'agit de la technique la plus couramment employée depuis de nombreuses années, ces courbes et les données correspondantes existent déjà. La valeur de contrainte utilisée avec la courbe dépend des données représentées sur la courbe et, dans une certaine mesure, du bon vouloir de l'ingénieur. La version uniaxiale de l'assistant de fatigue utilise la "pire contrainte principale absolue" dans ses calculs, car cela suppose que la direction des contraintes est constante.
L'assistant de fatigue génère la courbe SN en interne à partir des données de matériau saisies par l'ingénieur. Les données requises sont la résistance à la traction monotone du matériau et une limite d'endurance.
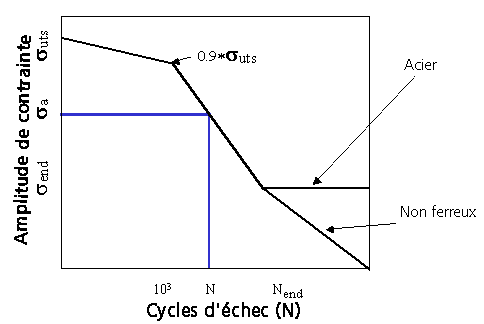
Figure 3 : Courbe SN
La courbe SN se présente comme illustré sur la figure 3. Elle est toujours tracée sur un graphique logarithmique, comme indiqué. La courbe démarre à la résistance ultime à la traction spécifiée (SUTS) monotone au niveau de log(N)=1. Il est courant d'estimer l'amplitude à une valeur de 1 000 cycles par une ligne droite avec une valeur de 90 % de SUTS. La pente principale de la courbe SN s'étend du point de cycle 1 000 à une valeur de longévité correspondant à la limite d'endurance et à l'amplitude de contrainte équivalent à envoyer. Le comportement au-delà de la limite d'endurance diffère selon qu'il s'agit d'un matériau ferreux ou d'un alliage non ferreux. Par défaut, les aciers présentent une limite d'endurance réelle et un aplatissement de la courbe SN. A l'inverse, les alliages d'aluminium et les alliages non ferreux présentent un aplatissement moins marqué de la courbe SN à des cycles élevés. L'assistant de fatigue permet à l'utilisateur de faire la distinction entre ces deux cas.
Effets de contrainte moyenne
En général, vous présentez les courbes SN pour une analyse inverse complète. Cela signifie que les contraintes appliquées alternent états de traction égale et états de compression. Dans le cas d'une charge structurelle réaliste, il est courant que les charges cycliques oscillent autour d'un état moyen différent de zéro. Cet état n'a pas d'effet notable sur la longévité avant défaillance. Une méthode est requise pour prendre en compte la présence d'une contrainte moyenne dans le cycle lors de l'utilisation de données SN standard.
L'assistant de fatigue vous permet de calculer l'endurance à l'aide de corrections "non moyenne", de Gerber et de Goodman.
Concentration de contraintes
Les analyses par éléments finis ont tendance à expliciter le modèle et à calculer les contraintes dans les zones de concentration locale. Par conséquent, la mise à l'échelle de la contrainte nominale n'est probablement pas nécessaire. Toutefois, si une mise à l'échelle linéaire est requise pour les contraintes EF calculées, l'assistant de fatigue fournit un facteur d'échelle général Kt.
se = Kt.snominal
où se = contrainte d'élasticité mise à l'échelle
Modificateurs de limite d'endurance
Les données de courbe SN sont généralement présentées à partir des tests réalisés sur des échantillons polis de taille standard. L'application de ces données de tests de "laboratoire" à des composants réels requiert parfois une correction. Les corrections prennent habituellement la forme de "modificateurs", qui sont appliqués à la limite d'endurance des échantillons.
Il est possible d'appliquer des modificateurs pour prendre en compte la taille, la finition de surface, l'inclinaison de la contrainte, les traitements de surface, le type de charge, etc. Ces modificateurs sont largement décrits dans la plupart des textes techniques et à disposition immédiate de l'ingénieur si nécessaire.
send-modified = send . nsize . nsurface …
où n est le modificateur approprié.
L'assistant de fatigue fournit des modificateurs standard pour les effets de finition de surface et les effets statistiques, ainsi qu'un modificateur général pour entrer une valeur combinée calculée. Il modifie la courbe SN en mettant à l'échelle la limite d'endurance des échantillons (comme illustré ci-dessus) et en effectuant une rotation de la courbe SN au 1 000e point de cycle.
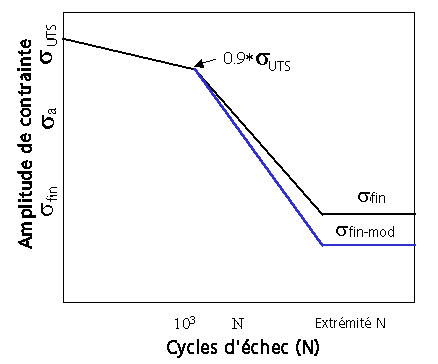
Figure 4
Technique de longévité par déformation
La technique de longévité par déformation a été développée dans les années 1960 en tant qu'amélioration de la technique de longévité par contrainte afin de prévoir l'endurance des matériaux, qui subissent une déformation plastique. Le principe est le même : l'amplitude de déformation (et non plus de contrainte) est mesurée ou calculée pour une charge cyclique, puis comparée à un graphique empirique mettant en corrélation l'amplitude de déformation et la longévité. Cette technique présente un avantage sur la méthode de longévité par contrainte : à aucun moment dans les données de tests il n'existe l'hypothèse d'une déformation élastique totale.
Courbes de longévité par déformation
Les courbes de longévité par déformation décrivent la fatigue des échantillons testés en laboratoire. Ces échantillons sont généralement testés sous une charge contrôlée de déformation inversée complète et mis en rapport avec la longévité jusqu'à l'apparition des fissures. La courbe empirique d'amplitude de déformation par rapport aux cycles avant défaillance est tracée.
A de faibles niveaux de déformation (où celle-ci est parfaitement élastique), le comportement de fatigue correspond à l'amplitude de contrainte et
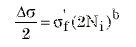
où sf' est le coefficient de la résistance à la fatigue et b est l'exposant de résistance à la fatigue, tous deux extraits de l'ajustement log-log de l'amplitude de contrainte par rapport à la longévité.
A des niveaux élevés de déformation (où celle-ci est principalement plastique), le comportement de fatigue correspond mieux à une amplitude de déformation telle que

où ef' est le coefficient de la ductilité de fatigue et b est l'exposant de ductilité de fatigue, tous deux extraits de l'ajustement log-log de l'amplitude de déformation plastique par rapport à la longévité.
La courbe de longévité par déformation générale ou courbe de Coffin-Manson est ensuite décrite comme une combinaison de ces deux courbes linéaires individuelles, comme suit :
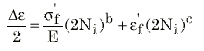
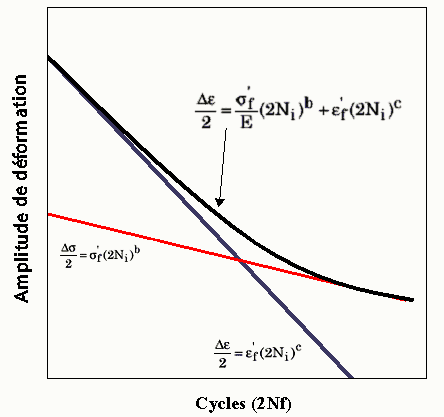
Figure 5 : Courbe de longévité par déformation à amplitude constante Relation de Coffin-Manson.
Approximation de différents coefficients de longévité par déformation indisponibles
Il existe plusieurs méthodes pour obtenir des données de matériaux approximatives basées sur la déformation à partir de données monotones plus facilement accessibles, telles que la résistance à la traction, le module, etc. La méthode utilisée par l'assistant de fatigue est celle de Seeger/Beste. Elle est référencée dans de nombreux textes traitant du calcul de la fatigue basé sur la déformation. Cette technique crée une approximation de la courbe de longévité par déformation (coefficients basés sur la déformation) à l'aide de la formule suivante :
Aciers :
- K' = 1.65 * UTS
- n' = 0.15
- Sf = 1.5 * UTS
- b= -0.087
- c= -0.58
- Ef = 0.59 (si UTS/E<0.003)
- Ef = 0.59*(1.375-125*UTS/E)
Autres :
- K' = 1.61 * UTS
- n' = 0.11
- Sf = 1.67 * UTS
- b= -0.095
- c= -0.69
- Ef = 0.535
Correction de contrainte moyenne
La courbe de longévité à amplitude constante décrite précédemment est générée lors de tests des matériaux sous une charge inversée complète, c'est-à-dire avec un décalage moyen nul. Dans les cycles de charge d'ingénierie réalistes, il existe inévitablement une contrainte moyenne non nulle.
Pour corriger l'existence de moyennes non nulles dans le cycle de déformation, l'assistant de fatigue applique deux corrections à la courbe de longévité par déformation simple : la correction de Morrow et la correction de Smith-Watson-Topper.
Courbe de longévité par déformation avec correction de Morrow

Courbe de longévité par déformation avec correction de Smith-Watson-Topper
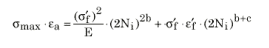
Données de matériau élasto-plastique
Dans la mesure où les données de longévité par déformation sont extraites des matériaux, eux-mêmes soumis à une charge cyclique au-delà de la limite d'élasticité, il est nécessaire de définir une courbe de matériau avec contrainte/déformation cyclique.
L'assistant de fatigue utilise deux formules empiriques bien documentées pour définir une courbe de contrainte/déformation avec des cycles stables.
La courbe de contrainte/déformation cyclique est construite à l'aide de la relation de Ramberg-Osgood pour déterminer les constantes de matériau K' et n'. Il s'agit respectivement du coefficient de durcissement cyclique et de l'exposant de durcissement cyclique.
Relation de Ramberg-Osgood
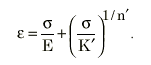
Pour générer une courbe de contrainte/déformation cyclique complète, la théorie de Masing est utilisée comme suit :

Par combinaison de ces deux relations, il est possible de générer une boucle d'hystérésis pour la courbe de contrainte/déformation à cycles stables à partir des deux constantes de matériaux.
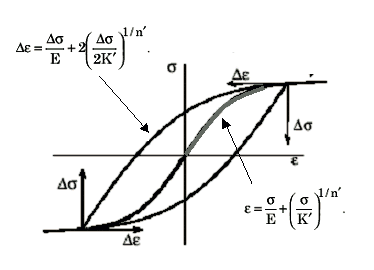
Figure 6 : Courbe de contrainte/déformation à cycles stables
Correction de Neuber
De nombreux codes de fatigue basés sur des éléments finis utilisent les résultats des analyses EF d'élasticité. Cela permet d'effectuer des calculs EF relativement simples sans consacrer votre temps et votre budget à des solutions non linéaires. Si vous envisagez de calculer ultérieurement la longévité basée sur les déformations à l'aide de ces contraintes d'élasticité, définissez une méthode pour convertir la contrainte d'élasticité EF en contrainte (et déformation) élasto-plastique équivalente.
Parmi les nombreuses méthodes proposées pour cette conversion, l'assistant de fatigue utilise la plus courante : la correction de Neuber.
Approche de longévité par contrainte
- Lire les données de contrainte d'élasticité à partir des résultats EF
- Extraire la pire contrainte principale absolue
- Mettre à l'échelle les contraintes d'élasticité via Kt
- Extraire les cycles de l'historique temporel de la charge via un comptage rainflow
- Modifier la courbe SN en fonction des modificateurs de limite d'endurance
- Calculer l'avarie pour les cycles dotés d'une correction de contrainte moyenne
- Ajouter l'avarie conformément à la règle linéaire de Miners
- Obtenir l'endurance et le facteur de sécurité de tous les noeuds
Approche de longévité par déformation
- Lire les données de contrainte d'élasticité à partir des résultats EF
- Extraire la pire contrainte principale absolue
- Mettre à l'échelle les contraintes d'élasticité via Kt
- Effectuer la correction Neuber sur la contrainte locale
- Créer un historique temporel complet des contraintes et déformations localisées à l'aide des courbes de contrainte/déformation à cycles stables
- Extraire toutes les boucles d'hystéréris fermées dans l'historique temporel
- Créer une courbe de longévité par déformation à cycle unique à partir des données de matériau
- Modifier les courbes de longévité par déformation en fonction des modificateurs de limite d'endurance
- Calculer l'avarie pour les cycles dotés d'une correction de contrainte moyenne
- Ajouter l'avarie conformément à la règle linéaire de Miners
- Obtenir l'endurance et le facteur de sécurité de tous les noeuds