なし
このオプションを選択すると、モデルから結果コンターが削除され、シェーディングおよびメッシュ ラインに対して既定の色が使用されます。
変位
このオプションを選択すると、モデルに変位がカラー表示されます。使用できるコマンドは次のとおりです。
- [大きさ]: 変位の大きさを表示の基準として設定できます。大きさの値は常に正です。大きさとは、節点が移動した距離全体のことを指します。mag = sqrt[(dX)^2 + (dY)^2 + (dZ)^2]
- [X]: 変位ベクトルと X 軸方向の単位ベクトルとのドット積を表示の基準として設定できます。この場合表示されるのは、変位の X 軸方向の成分です。
- [Y]: 変位ベクトルと Y 軸方向の単位ベクトルとのドット積を表示の基準として設定できます。この場合表示されるのは、変位の Y 軸方向の成分です。
- [Z]: 変位ベクトルと Z 軸方向の単位ベクトルとのドット積を表示の基準として設定できます。この場合表示されるのは、変位の Z 軸方向の成分です。
- [ベクトル プロット]: 変位の大きさを表示の基準として設定できます。結果は各節点に描画されるベクトル(矢印)として表示されます。矢印の長さおよび色により変位の大きさが表され、矢印の方向により変位ベクトルの方向が表されます。[表示オプション] > [プロット設定] > [ベクトル プロット]タブでは、矢印のサイズを調整できます。
回転
このオプションを選択すると、モデルに各節点の回転がカラー表示されます。この結果が有効なのは、回転に対して抵抗できる要素上の節点に対してのみです。たとえば、ブリック要素上の節点は自由度が並進方向の 3 つしかないため、回転方向の変位は計算されません。ビーム要素上の節点は、3 方向の回転に対して抵抗できます。プレート要素上の節点は、面内の 2 方向の回転に対して抵抗できます。使用できるコマンドは次のとおりです。
- [大きさ]: 回転変位の大きさを表示の基準として設定できます。大きさの値は常に正です。大きさとは、節点が回転した距離全体のことを指します。mag = sqrt[(rX)^2 + (rY)^2 + (rZ)^2]
- [X]: 回転ベクトルと X 軸方向の単位ベクトルとのドット積を表示の基準として設定できます。この場合表示されるのは、回転の X 軸周りの成分です。
- [Y]: 回転ベクトルと Y 軸方向の単位ベクトルとのドット積を表示の基準として設定できます。この場合表示されるのは、回転の Y 軸周りの成分です。
- [Z]: 回転ベクトルと Z 軸方向の単位ベクトルとのドット積を表示の基準として設定できます。この場合表示されるのは、回転の Z 軸周りの成分です。
複数の回転が関与している場合、大たわみ解析(MES または非線形解析)では、これらの結果は慎重に解釈する必要があります。回転の結果は、運動の履歴をすべて反映しており、したがって途中の経路に依存します。例として次の図を見てください。(変位の結果は途中経路に依存しません。)
 L 字型のビームが XZ 平面内に置かれているとします。 |
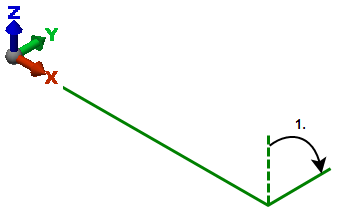 まず、このビームを X 軸の周りに 90 度回転します。 |
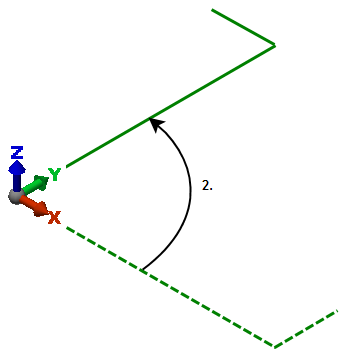 次に、ビームを Z 軸の周りに 90 度回転します。 |
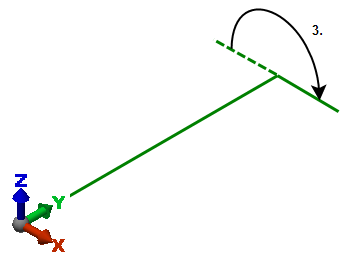 さらに、ビームを Y 軸の周りに 180 度回転します。 |
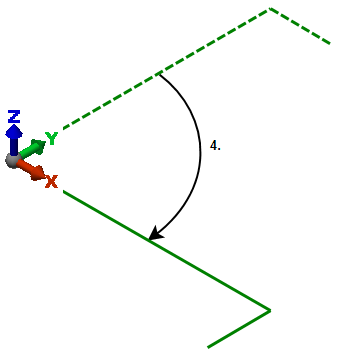 最後に、ビームを Z 軸の周りに 90 度回転します。
最初の位置と最後の位置とを比較すると、最終的な結果は、X 軸の周りに +90 度回転し Y 軸および Z 軸の周りには回転しなかった場合と実質的には同じです。大たわみ解析では、X 軸の周りに -90 度、Y 軸の周りに 180 度それぞれ回転し、Z 軸の周りには回転しなかったという結果になります。 変位の結果は途中経路に依存しないため、最終的には X 軸方向に 0、Y 軸方向および Z 軸方向にそれぞれ -L だけ変位したという結果になります。ただし、L は短い方の脚の長さです。 |
上記の例では、[回転剛体移動]オプション(ビーム要素の[要素定義]ダイアログで設定)を使用した場合とは異なり、ビームの方向が可視化されています。軸 2 および軸 3 の方向が正確なのは、[回転剛体移動]を使用している場合のみです。
変位と回転の正規化
- 固有値解析
応力
解析手法にはさまざまなものがあり、モデルが適切かどうかを判断する場合には有効な手段として利用できます。結果環境では、ローカル座標で表した応力やそれらの応力から導出されるさまざまな量が表示され、それらを介してこうした解析手法を使用することができます。導出される量としては、フォンミーゼス基準や トレスカ 基準、最大および最小の主応力、要素固有の出力などがあります。解析結果の精度は、作成するメッシュや適用する FEA パラメータによって異なるため、結果環境には共有節点で推定した精度が表示されます。モデルが適切かどうかは、この精度値を基に判断することができます。
計算
ソフトウェアでは、節点に対する応力に基づいて、応力の推定値が計算されます。補外を行う場合は、節点の応力を基にした計算値の方が、要素内部の応力に基づく計算値よりも精度が高くなります。節点での応力値は要素全体に対する応力の計算値よりも扱いやすいため、節点での応力を表示した方が、荷重下のモデルをより実際的かつ簡便な形で表現することができます。
要素に対して計算された応力により、ガウス点における応力についての情報が得られます。ガウス点とは、有限要素解と理論上の解がほぼ一致する数値積分点です。従来の手法では、2D 要素の中心または面、および 3D 要素の図心を基準にしてこれらの応力が平均化されるため、隣接する要素間に比較的大きな差があれば、それを明示することができます。有限要素解は連続関数の近似であり、それらの位置に基づいて得られる結果は精度が低いため、応力下でのモデルの挙動を正確に捉えることができない場合があります。
個々の節点で応力を計算すれば、この問題は解消されます。ローカル最小二乗法を使用すると、ガウス点から対象の節点に対して応力が補外されます。解析対象のパーツの表面またはエッジの上にある節点は通常、モデルの重要な領域であるため、それらの節点における応力を精密に推定することは非常に重要です。異なる要素間で節点が共有されている場合は、精度に関する情報も取得できます。
モデルの表面を表示すると、その表面を定義するメッシュの各要素における個々の点での強さまたは応力が計算され、その点に適切な表示値が割り当てられます。さらに、その表面を表示するための縮尺が検証された後、各点に対しその計算値を基にして適切な色および陰影が選択されます。使用している表示方法に従って、表面がシェーディングされたモデルが再描画されます。結果環境では、平滑化など、モデルの表示方法を制御するための表示オプションを選択できます。これらのオプションを使用することにより、それぞれの目的に最も適した方法でモデルを表示することができます。
[フォンミーゼス]
このコマンドを使用すると、等価応力である フォンミーゼス応力が表示またはデータ出力の対象となるように結果画面を設定できます。フォンミーゼス応力は、面積を持つ要素タイプ(2D 、プレートなど)および体積を持つ要素タイプ(ブリック)に対して表示できます。
計算式は次のとおりです。
ただし、S x 、S y 、および S z は全体座標系における軸方向応力、S xy 、S yz 、および S xz はせん断応力です。次のように、主応力 S 1 、S 2 、および S 3 を使用して表すこともできます。
これらの計算式から分かるように、フォンミーゼス応力の値は常に正です。
[トレスカ*2]
トレスカ*2 応力は、面積を持つ要素タイプ(2D 、プレートなど)および体積を持つ要素タイプ(ブリック)に対して表示できます。この方法を使用すると、次の応力テンソルから最大せん断応力を抽出できます。トレスカ の計算式は次のとおりです。
ただし、S1、S2、および S3 は主応力です。レポートされる値は、最大せん断応力の 2 倍です。そのため、レポートされた トレスカ*2 値が降伏応力に達すれば、降伏が生じます。定義により、トレスカ応力の値は常に正です。図については、「モールの応力円」を参照してください。トレスカ*2 は、応力強さとも呼ばれます。
[最小主応力]
このコマンドを使用すると、表示またはデータ出力の対象として最小主応力(S3)を計算するように結果画面を設定できます。この主応力は、面積を持つ要素タイプ(2D、プレートなど)および体積を持つ要素タイプ(ブリック)に対して表示できます。符号が正(+)の場合は引張を表し、符合が負(-)の場合は圧縮を表します。図については、「モールの応力円」を参照してください。
[最小主応力(ベクトル)]
このコマンドを使用すると、各要素における最小主応力の方向をベクトル プロットとして表示できます。要素の各節点におけるテンソルが平均化され、その平均化されたテンソルの最小主応力(ベクトル)が要素の図心にプロットされます。いずれかの要素を選択し、さらに[結果の照会]
[照会] [現在の結果]を選択すると、このベクトルの成分がすべて表示されます。
[中間主応力]
このコマンドを使用すると、表示またはデータ出力の対象として中間主応力(S2)を計算するように結果画面を設定できます。中間主応力は、最小主応力と最大主応力の双方に対して垂直な方向の応力です。この主応力は、面積を持つ要素タイプ(2D、プレートなど)および体積を持つ要素タイプ(ブリック)に対して表示できます。符号が正(+)の場合は引張を表し、符合が負(-)の場合は圧縮を表します。
[中間主応力(ベクトル)]
このコマンドを使用すると、各要素における中間主応力の方向をベクトル プロットとして表示できます。要素の各節点におけるテンソルが平均化され、その平均化されたテンソルの中間主応力(ベクトル)が要素の図心にプロットされます。いずれかの要素を選択し、さらに[結果の照会] [照会] [現在の結果]を選択すると、このベクトルの成分がすべて表示されます。
[最大主応力]
このコマンドを使用すると、表示またはデータ出力の対象として最大主応力(S1)を計算するように結果画面を設定できます。この主応力は、面積を持つ要素タイプ(2D、プレートなど)および体積を持つ要素タイプ(ブリック)に対して表示できます。符号が正(+)の場合は引張を表し、符合が負(-)の場合は圧縮を表します。図については、「モールの応力円」を参照してください。
[最大主応力(ベクトル)]
このコマンドを使用すると、各要素における最大主応力の方向をベクトル プロットとして表示できます。要素の各節点におけるテンソルが平均化され、その平均化されたテンソルの最大主応力(ベクトル)が要素の図心にプロットされます。いずれかの要素を選択し、さらに[結果の照会] [照会] [現在の結果]を選択すると、このベクトルの成分がすべて表示されます。
[テンソル]
このコマンドを使用すると、選択した方向に対する応力の成分を表示できます。数学的には、応力テンソルとのドット積またはローカル座標系での応力テンソルの成分が使用されます。応力テンソルは、面積を持つ要素タイプ(2D、プレートなど)および体積を持つ要素タイプ(ブリック)に対して表示できます。
[結果コンター] [設定] [要素のローカル結果を使用]がオンになっていない場合は、次のグローバル応力の中からいずれかを選択することができます。このオプションがオンの場合は、選択する項目に応じて、個々の説明の中で言及されているローカル座標系での応力テンソルが表示されます。
ローカル座標軸を持つ要素であっても、ローカル座標軸の方向が隣接する要素によって異なる場合は、応力の平滑化(平均化)が意味を持たないこともあります。平滑化応力テンソルの値が意味を持つのは、ローカル座標軸の方向が、ある要素から次の要素へ向かう方向と一致している場合のみです。
- 1) XX 全体座標系の X 軸方向の垂直応力を表す応力テンソルの成分。符号が正(+)の場合は引張を表し、符合が負(-)の場合は圧縮を表します。[結果コンター] [設定] [要素のローカル結果を使用]がオンの場合は、ローカル座標系での応力テンソルの 1-1 成分が表示されます。
- 2) YY 全体座標系の Y 軸方向の垂直応力を表す応力テンソルの成分。符号が正(+)の場合は引張を表し、符合が負(-)の場合は圧縮を表します。[結果コンター] [設定] [要素のローカル結果を使用]がオンの場合は、ローカル座標系での応力テンソルの 2-2 成分が表示されます。
- 3) ZZ 全体座標系の Z 軸方向の垂直応力を表す応力テンソルの成分。符号が正(+)の場合は引張を表し、符合が負(-)の場合は圧縮を表します。[結果コンター] [設定] [要素のローカル結果を使用]がオンの場合は、ローカル座標系での応力テンソルの 3-3 成分が表示されます。
- 4) XY 全体座標系の XY 方向のせん断応力を表す応力テンソルの成分。(X は面に対して垂直な方向、Y はせん断応力の方向を表します。)[結果コンター] [設定] [要素のローカル結果を使用]がオンの場合は、ローカル座標系での応力テンソルの 1-2 成分が表示されます。
- 5) YZ 全体座標系の YZ 方向のせん断応力を表す応力テンソルの成分。(Y は面に対して垂直な方向、Z はせん断応力の方向を表します。)[結果コンター] [設定] [要素のローカル結果を使用]がオンの場合は、ローカル座標系での応力テンソルの 2-3 成分が表示されます。
- 6) ZX 全体座標系の ZX 方向のせん断応力を表す応力テンソルの成分。(Z は面に対して垂直な方向、X はせん断応力の方向を表します。)[結果コンター] [設定] [要素のローカル結果を使用]がオンの場合は、ローカル座標系での応力テンソルの 3-1 成分が表示されます。
[ビームとトラス]
このコマンドを使用すると、線形トラス要素、非線形トラス要素、線形ビーム要素、非線形ビーム要素、およ非線形パイプ要素に対する応力を表示できます。表示できる結果は次のとおりです。
- 塑性を持つビーム要素を対象とする非線形解析の場合、このコマンドを使用して表示される結果は、降伏強さによって部分的にのみ修正されます。それぞれの応力(軸応力、ローカル 2 の曲げ応力、およびローカル 3 の曲げ応力)は、必要に応じてキャップされるか、降伏応力に限定されます。その後、最悪応力によって 3 つの結果がまとめて追加されます。
- 応力についてより正確な結果を得るには、解析を実行する前に、ビームの[要素定義]にある[応力とひずみのバイナリ出力]オプションをオンにしてください。結果環境で、[結果の照会][照会][詳細なビーム応力]および[結果の照会][照会][ビームひずみの詳細]を使用すると結果を確認できます。
- [Axial Stress (Local 1 Direction)]: 軸方向応力が表示されます。これは、軸方向の力を断面積で割った値として計算されます。値が正の場合は引張応力であり、値が負の場合は圧縮応力です。
- [Bending Stress in Local 2 Direction]: ビーム要素においてローカル軸 2 周りの曲げモーメントによる曲げ応力が表示されます。これは、軸 2 の周りの曲げモーメントをローカル軸 2 の周りの断面係数で割った値として計算されます。ローカル軸 2 は k 要素を通り、ビームに直交します。(トラス要素は曲げることができないため、このメニュー項目の適用対象とはなりません。)
- [Bending Stress in Local 3 Direction]: ビーム要素においてローカル軸 3 の周りの曲げモーメントによる曲げ応力が表示されます。これは、軸 3 の周りの曲げモーメントをローカル軸 3 の周りの断面係数で割った値として計算されます。ローカル軸 3 は、ローカル軸 1 に沿うベクトルとローカル軸 2 に沿うベクトルとのクロス積により定義されます。(トラス要素は曲げることができないため、このメニュー項目の適用対象とはなりません。)
- [最悪]: 1 つの角では、軸方向応力、軸 2 の周りの曲げ応力、および軸 3 の周りの曲げ応力の組み合わせにより絶対値は最大となります。これがビームの最悪の応力です。線形応力の場合、符号が正(+)であれば、ビームに対して軸方向の引張が作用していることを表し、符号が負(-)であれば、ビームに対して軸方向の圧縮が作用していることを表しています。数式で表すと次のようになります。
最悪の応力 = (P/A の符号)(ABS(P/A)+ABS(M2/S2)+ABS(M3/S3))
応力解析(線形および非線形)では、(S2 および S3 の入力値または計算値はただ 1 つであるため)断面は対称であると仮定されます。したがって非対称のビームの場合、数式の上では、図 1 の左下角や左上角のように実在しない場所に最悪の応力が生じる場合があります。
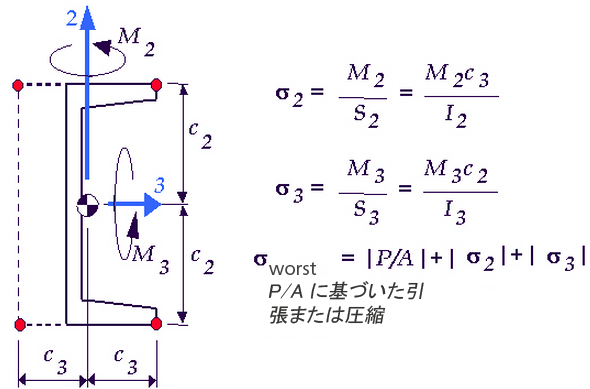
図 1: 非対称のビームにおける応力の結果
C2 と C3 は等しいと仮定されているため(S2 および S3 の入力値はただ 1 つであるため)、実在しない場所に最悪の応力が生じることは可能です。
ビーム要素に対してローカル軸 1、ローカル軸 2、およびローカル軸 3 を表示する場合は、[結果オプション][表示][要素方向]を使用します。
コンポジット
[破壊インデックス]
このコマンドを使用すると、［要素定義］ダイアログで設定した面内複合材料の破壊判定基準([Tsai-Wu]、[最大応力]、または[最大ひずみ])に対応する結果が表示されます。
(隣接する要素間で値を平滑化または平均化する代わりに)各要素における実際の破壊判定基準値を表示できるように、平滑化([結果コンター][設定][結果を平滑化])は無効にすることをお勧めします。
[結果コンター] [応力] [複合材料] [オプション]を使用すれば、どの薄板に結果を表示するかを制御することができます。また、このコマンドを使用すると、[最悪]の結果が表示されるよう選択することもできます。
最大応力および最大ひずみが破壊判定基準の場合は、最初に薄板の上面および底面に基づいて、次のような安全係数を考えます。
最大応力 - 安全係数
、
、
、
、および 
ただし、σ は方向 1 または方向 2 の垂直応力の計算値、X および Y は方向 1 および方向 2 の許容できる応力(応力の計算値に対応する圧縮または引張)、τ 12 ·はせん断応力の計算値、S は許容できるせん断応力です。
最大ひずみ - 安全係数
、
、
、
、および 
ただし、ε は方向 1 または方向 2 の垂直ひずみの計算値、T は方向 1 および方向 2 の許容できるひずみ(ひずみの計算値に対応する圧縮または引張)、γ 12 ·はせん断ひずみの計算値、S は許容できるせん断ひずみです。
このときに表示される結果は次のとおりです。
| 最大応力および最大ひずみの破壊インデックス | |
|---|---|
| 線形応力 | 非線形応力 |
| 1/安全係数の計算値 | 安全係数の計算値 |
| 最大値のプロット | 最小値のプロット |
| 破壊を表す 1 より大きな値 | 破壊を表す 1 より大きな値 |
Tsai-Wu が破壊判定基準の場合は、最初に次のような 値 F を考えます。
ここで
σ および τ·は垂直応力およびせん断応力の計算値、それ以外の値はすべて材料の入力値です。
このときに表示される結果は次のとおりです。
| Tsai-Wu の破壊インデックス | |
|---|---|
| 線形応力 | 非線形応力 |
| 値 F のプロット | 値 1/F のプロット |
| 破壊を表す 1 より大きな値 | 破壊を表す 1 より大きな値 |
[面外破壊]
最大応力を破壊判定基準として、厚肉複合材要素を使用している場合、このオプションを使用すると、コア薄板の厚み(面外方向)を基にして破壊判定基準を表示することができます。プロットされる結果は、次の各量の最大値です。
、
、および 
ただし、σ core はコア(3 の方向)の垂直応力の計算値、Z c は許容されるコアの圧縮応力、τ はせん断応力の計算値、S は許容される横せん断応力です。
破壊が発生するのは、値が 1 より大きな場合です。
ひずみ
これまでの説明や計算式の中に現れる「応力」を「ひずみ」に読み替えれば、応力の結果に関する計算式の多くは、モデルにおけるひずみの結果を表示するのにも利用できます。以降の記述のうちこれに該当する部分には、対応するページへのリンクが記載されています。以下では、ひずみに関するコマンドのうち、等価応力のコマンドと大きな違いがあるものについて詳しく説明します。
- [フォンミーゼス]: フォンミーゼス式に基づいて等価ひずみを表示します。詳細については、フォンミーゼス応力に関する説明を参照してください。
- [トレスカ*2]: トレスカひずみ値の2倍を計算して等価ひずみを表示します。詳細については、トレスカ応力に関する説明を参照してください。
- [最小主ひずみ]: 最小主ひずみを表示します。詳細については、最小主応力に関する説明を参照してください。
- [最大主ひずみ]: 最大主ひずみを表示します。詳細については、最大主ひずみに関する説明を参照してください。
- [テンソル]: ひずみについて、選択した方向の成分を表示します。線形材料モデルを対象とした静解析の場合、ひずみは(応力と同じように)要素座標系、全体座標系、または円筒座標系で表示できます。 注: MES 解析の場合、ひずみテンソルの結果ではなく、公称ひずみの結果を表示できます。次の行列は公称ひずみ(MES)を表します。一方、ひずみテンソル(線形)は次の式で得られます。
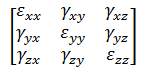
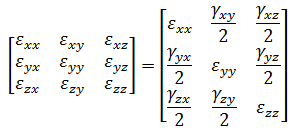
- [ビームとトラス]: ビーム要素およびトラス要素のひずみに関するメニューには、次のようなオプションがあります。
- [軸]: ビーム/トラスの軸に沿った過重による軸方向ひずみを表示します。引張ひずみを正とします。
- [軸 2 に関する曲げ]: 軸 2 の周りのモーメントによる縁ひずみを表示します。ビームに対してのみ有効です。引張ひずみを正とします。
- [軸 3 に関する曲げ]: 軸 3 の周りのモーメントによる縁ひずみを表示します。ビームに対してのみ有効です。引張ひずみを正とします。
- [最悪の組み合わせ]: ビーム要素に対しては、軸方向ひずみ、軸 2 の周りの曲げひずみ、および軸·3 の周りの曲げひずみの最悪の組み合わせを表示します。数式で表すと次のようになります。
最悪のひずみ = (P/A の符号)(ABS(P/A)+ABS(軸 2 の周りのひずみ)+ABS(軸 3 の周りのひずみ))
トラス要素の場合、最悪のひずみは軸方向ひずみ(P/A)に等しくなります。
[ひずみエネルギー密度]
このコマンドを選択すると、ひずみエネルギー密度に従ってモデルをシェーディングすることができます。要素のひずみエネルギーは、荷重により要素が吸収したエネルギーとして定義されます。このエネルギーを体積あたりに換算したものが 
です。
応力とひずみの正規化
- 固有値解析
これらの結果の唯一の目的は、モデル内における相対的な応力分布およびひずみ分布を示す点にあります。つまり、応力およびひずみが最大または最小の領域を特定することはできますが、モード解析だけで結果を数値化することはできません。結果は特定の励振に尺度調整されないため、応力およびひずみの絶対値は意味を持ちません。
Autodesk Simulation Moldflow の結果
適用可能な場合、Autodesk Simulation Mechanical のモデルを Autodesk Simulation Moldflow Advisor または Insight にエクスポートして、射出成形処理をシミュレーションできます。Moldflow でのシミュレーションが完了すると、Autodesk Simulation Mechanical の結果環境で追加の結果を視覚化できます。これらの結果は、リボンの[結果コンター]タブの[Moldflow 結果]パネルで選択します。線形解析タイプの中で Moldflow の結果を表示できるのは、線形材料による静解析だけです。Moldflow の結果は、非線形材料による固有値解析を除く、すべての非線形構造解析でも表示できます。表示できる結果は次のとおりです。
- [残留応力テンソル]ドロップダウン メニューを使用して、6 つの応力テンソルの成分(XX、YY、ZZ、XY、YZ、および ZX)の中から 1 つを選択します。これらの成分は、Moldflow でのシミュレーションにおいて成形処理が完了した時点のキャビティ内のパーツの応力に基づきます。これらは、金型拘束が適用された状態における応力です。また、これらの残留応力により、金型からの解放後にパーツに変形が生じます。
- [CTE テンソル]ドロップダウン メニューを使用して、[線膨張係数]の 6 つの方向(XX、YY、ZZ、XY、YZ、および ZX)におけるテンソルの成分を選択します。これらは、Moldflow での解析の層に基づいた CTE の結果です。すべての材料について、6 つの CTE のテンソルの成分すべてが表示されるとは限りません。6 つの CTE の成分があるのは、異方性熱特定が定義された材料に限られます。
[要素変位]
[要素力およびモーメント]に表示される結果は主に、トラス要素、ギャップ要素、ビーム要素、境界要素などの線要素に関する結果です。
- [伸張]: このコマンドを使用すると、長さの変化分に基づいて、ギャップ要素、境界要素、トラス要素、またはバネ要素をカラー表示できます。ギャップ要素、トラス要素、およびバネ要素の場合、正の値は引張を表します。境界要素の場合、正の値は要素の圧縮を表します。
- [ねじれ]: このコマンドを使用すると、要素の回転に基づいて、境界要素をカラー表示できます。ねじれの方向は、要素に固定された節点から自由端に向かって右ネジが進むときに回転する方向とします。
[要素力およびモーメント]
[要素力およびモーメント]に表示される結果は主に、トラス要素、ギャップ要素、ビーム要素、境界要素などのライン要素に関する結果です。
- [軸方向の力]: すべてのタイプの線要素(トラス要素、ビーム要素、バネ要素、ギャップ要素、および境界要素)に対して、軸方向(ローカル軸 1 の方向)の力を表示します。トラス要素、バネ要素、およびギャップ要素の場合、正の値は引張、負の値は圧縮を表します。境界要素の場合、正の値は要素の圧縮、負の値は要素の引張を表します。ビーム要素の場合については、後述する「ビーム要素におけるローカル的な力およびモーメントの方向」を参照してください。
- [軸 2 のせん断力]: ビーム要素に対してローカル軸 2 の方向のせん断力を表示します。
- [軸 3 のせん断力]: ビーム要素に対してローカル軸 3 の方向のせん断力を表示します。
- [トルク]: ビーム要素のねじれ(ローカル軸 1 の周りのモーメント)および回転境界要素のねじれを表示します。境界要素の場合、モデルに固定された節点における要素のねじれの方向は、要素に固定された節点から自由端に向かって右ネジが進むときに回転する方向とします。ビーム要素の場合については、後述する「ビーム要素におけるローカル的な力およびモーメントの方向」を参照してください。
- [軸 2 を中心としたモーメント]: ビーム要素に対してローカル軸 2 の周りのモーメントを表示します。
- [軸 3 を中心としたモーメント]: ビーム要素に対してローカル軸 3 の周りのモーメントを表示します。
- [プレート曲げモーメント]: オンにすると、曲げモーメント テンソル
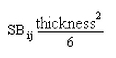
が、すべてのプレート応力の計算に使用されます。曲げモーメント テンソルは、分配モーメント(線モーメント、単位長さ当たりのモーメント)です。解釈が最も容易なのは、[結果コンター][応力][テンソル]で取得できる結果です。フォンミーゼス応力、トレスカ応力、最大主応力、および最小主応力の数値計算は実行されますが、その結果は曲げ応力の値と次の値との積に等しくなります。
.
ビーム要素におけるローカル的な力およびモーメントの方向
| [コンポーネント] | 構造ビーム |
|---|---|
| ローカル的な力 1 | 符号が正(+)の場合は引張、符合が負(-)の場合は圧縮を表す。 |
| ローカル的な力 2 |
|
| ローカル的な力 3 |
|
| ローカル的なモーメント 1 |
|
| ローカル的なモーメント 2 |
|
| ローカル的なモーメント 3 |
|
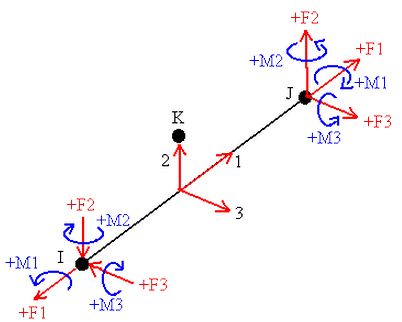
図 2: ビーム要素におけるローカル的な力およびモーメントの方向
[パワースペクトル密度]
ランダム応答解析の実行時にパワー スペクトル密度を出力するオプションが選択されている場合、結果の中には[パワースペクトル密度]という項目が表示されます。(オプションをオンにする方法については、「解析の設定と実行」>「線形」>「解析パラメータ」>「ランダム応答解析」を参照してください。)次の手順により、パワー スペクトル密度のグラフを作成することができます。
- 変位や応力など、モデルに関するいずれかの結果を表示します。
- パワー スペクトル密度が適切な節点を 1 つまたは複数選択し、右クリックして、[グラフの値]を選択します。
- グラフが作成されたら、[結果の照会][グラフ][パワースペクトル密度]を選択して、次のいずれかの結果を表示します。
- [X 方向変位]: X 方向の変位のパワー スペクトル密度を表示します。
- [Y 方向変位]: Y 方向の変位のパワー スペクトル密度を表示します。
- [Z 方向変位]: Z 方向の変位のパワー スペクトル密度を表示します。
- [X 方向回転]: X 方向の回転のパワー スペクトル密度を表示します。
- [Y 方向回転]: Y 方向の回転のパワー スペクトル密度を表示します。
- [Z 方向回転]: Z 方向の回転のパワー スペクトル密度を表示します。
ただし、これらの結果は支点を基準としたものです。これらは、入力された励振に関するパワー スペクトル密度を表します。
複数の節点がプロットされた場合、パワー スペクトル密度は各節点に対して個別に有効にする必要があります。パワー スペクトル密度を表示する場合は、事前にブラウザで目的の節点を右クリックし、[活性化]を選択してください。(一般的な手順については、「結果」>「結果環境」>「解析結果のグラフを作成する」を参照してください。)
[反力]
このコマンドを使用すると、内力および反力を表示することができます。表示される結果のタイプは次のとおりです。
- [内力]: 線形の場合、このメニューには各節点の内部反力が表示されます。これは支持反力ではないため、この場合は[残差力]コマンドを使用します。この反力は、大きさを表示することも、全体座標系の各軸方向の成分を表示することもできます。
- [印加力]: 各節点に印加された力が表示されます。この適用力は、大きさを表示することも、全体座標系の各軸方向の成分を表示することもできます。
- [反力(負)]: 各節点の残差力(印加力と反力の和)が表示されます。これを支持反力とみなすこともできます。ただしこの残差力は、モデルが周囲に及ぼす力です。つまり残差力と支持反力とは、互いに大きさは同じですが向きは反対です。この残差力は、大きさを表示することも、全体座標系の各軸方向の成分を表示することもできます。
MES/非線形の場合、このメニューには各節点の反力が表示されます。表示される結果は、境界条件、強制変位、衝突壁、および表面間接触においてゼロ以外の値を取ります。
- [内部モーメント]: 線形の場合、このメニューには各節点の内部反力モーメントが表示されます。これは支持反力ではないため、この場合は[残りの力のモーメント]コマンドを使用します。この反力モーメントは、大きさを表示することも、全体座標系の各軸方向の成分を表示することもできます。
- [適用されたモーメント]: 各節点に適用されたモーメントが表示されます。この適用されたモーメントは、大きさを表示することも、全体座標系の各軸方向の成分を表示することもできます。
- [反モーメント(負)]: 各節点の残差モーメント(適用されたモーメントと反力モーメントの和)が表示されます。これを支持反力モーメントとみなすこともできます。ただしこの残差モーメントは、モデルが周囲に及ぼすモーメントです。つまり残差モーメントと支持反力モーメントとは、互いに大きさは同じですが向きは反対です。この残差力は、大きさを表示することも、全体座標系の各軸方向の成分を表示することもできます。
MES/非線形の場合、このメニューには各節点の反力モーメントが表示されます。表示される結果は、境界条件および強制変位においてゼロ以外の値を取ります。
それぞれの結果に対して、次のオプションを使用できます。
- [大きさ]: 結果の大きさに基づいてモデルをシェーディングします。
- [X]: 結果の X 成分に基づいてモデルをシェーディングします。
- [Y]: 結果の Y 成分に基づいてモデルをシェーディングします。
- [Z]: 結果の Z 成分に基づいてモデルをシェーディングします。
- [ベクトル プロット]: 各節点に結果を矢印で表示します。矢印の長さおよび色により結果の大きさが表され、矢印の方向により結果のベクトルの方向が表されます。 注: 反力/反力モーメントおよび残差力/残差モーメントは、スマート接着により接続された節点ではゼロ以外の値を取ります。(これらの結果は通常、パーツ間の境界で 0 になります。)
[フォンミーゼスの精度]
[精度]を使用すると、要素間における結果の不連続的な変化を明確にすることができます。理想的なモデルの場合、応力は隣接する要素間で滑らかに変化します。モデルをいくつかの要素で離散化するプロセスでは、要素間で結果に何らかの変化が生じ、かつその変化は不連続的です。
応力モデルを例にとると、共有節点を持つ要素では各節点での応力を個別に予測することができるため、それぞれに独立した応力の計算値により、フォンミーゼス応力を基にしてモデルの精度を推定することができます。各節点における精度値は次の式に基づいて計算されます。
定義により、精度値の範囲は 0(最高精度)～ 0.5(最低精度)です。2 つ以上の要素間で共有されていない節点では、推定される応力はただ 1 つであり、したがって精度値は 0 です。
例 1:
モデル内の フォンミーゼス応力の最大値が 200 の場合、各節点(最大 3 つの要素が接続された節点)での精度は次のようになります。
| 節点番号 | フォンミーゼス応力 | 精度値 | コメント | ||
| 値 1 | 値 2 | 値 3 | |||
| 17 | 20 | -- | -- | .0 | 要素がただ 1 つである節点 |
| 23 | 20 | 40 | 25 | .05 | .5(40-20)/200 |
| 36 | 150 | 120 | 200 | .20 | .5(200-120)/200 |
例 2:
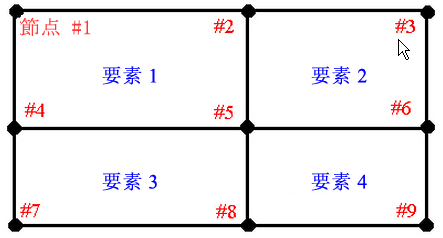
次の図のように節点 #5 の周囲に 4 つの要素があるとし、節点 #5 における各要素の応力が下記の表のように与えられているとします。
| 要素番号 | 節点番号 | フォンミーゼス応力 |
| 1 | 5 | 20,000 |
| 2 | 5 | 15,000 |
| 3 | 5 | 19,000 |
| 4 | 5 | 10,000 |
モデル内の応力が(たとえば節点 9 で)最大値 25,000 をとるとすると、節点 5 における精度は次のようになります。
節点 5 の精度 = 0.5(20,000 - 10,000)/25,000 = 0.20
ただし、実際の応力がこの範囲内に値をとる保証はありません。実際の応力がどの範囲に値をとるかについては、モデルのメッシュがどの程度適切に作成されているかや、実際のパーツがどの程度適切にモデル化されているかによって決まります。誤差がある場合でも、それが指定された精度の範囲内であれば許容されます。たとえば、精度値が 0.1、最大応力が 200 の場合、20 未満の誤差は許容範囲であるとみなされます。
[適用荷重]
このオプションを選択すると、入力された荷重がモデルに表示されます。構造解析に使用できる荷重は温度および電圧です。
- 線形応力解析については、次のことが当てはまります。
- [結果コンター][その他の結果][適用荷重][温度]は、常に使用可能です。
- モデル ファイル、定常熱伝導解析、または非定常熱伝導解析で[解析パラメーター]に指定されたすべてのタイプの温度荷重に対してコンターが表示されます。
- 温度が解析に与える影響は、応力なしの参照温度および熱乗数によって決まります。ただし、これらの寄与度は温度コンターには表示されません。
- [結果コンター]
- メカニカル イベント シミュレーション/非線形応力解析については、次のことが当てはまります。
- [結果コンター][その他の結果][適用荷重][温度]は、[解析パラメータ]で節点温度のソースがモデルに割り当てられている場合にのみ使用可能です。
- コンターは、モデル ファイルの温度荷重に対してのみ表示されます。定常熱伝導解析および非定常熱伝導解析の温度コンターは、プロットには使用できません。
- 温度が解析に与える影響は、応力なしの参照温度および荷重曲線乗数によっても決まります。荷重曲線乗数の寄与度は温度コンターに表示されます。
- [結果コンター]
[要素プロパティ]
ここに含まれるコマンドを使用すると、要素の形状に基づいてモデルをシェーディングすることができます。これらのコマンドはそのほとんどが、2D 要素、プレート要素、ブリック要素など、面積または体積を持つタイプの要素に対してのみ有効です。
次の各オプションを使用すると、選択した項目を基準としてモデルをシェーディングすることができます。
- [体積]: モデルに対して[解析][解析][重量と図心]を実行する必要がある場合は、[結果コンター][その他の結果][要素プロパティ][体積]コマンドを選択することにより、各要素の体積を表示することができます。[照会] > [結果]ダイアログで重み付き結果サマリーが計算される場合、[重量と図心]は自動的に実行されます。
- [ねじれ角]: 4 辺形(4 節点)要素の反りまたはソリッド要素の 4 節点面の反りが表示されます。ねじれ角は、3 つの方法で計算できます。
- [最小曲げ角法]または[最大曲げ角法]: どちらか一方のコマンドを選択すると、4 辺形の 2 つの曲げ角度が計算され、最小曲げ角度または最大曲げ角度が使用されます。4 辺形の曲げ角度は、4 辺形を 2 つの 3 角形に分割する(2 つの対角線のどちらか一方を追加する)ことで得られます。曲げ角度は、分割してできた 2 つの 3 角形の法線がなす角度です。
- [中立面法]: この場合、中立面の角度の正弦は、中立面の上に位置する任意の端節点の高さを最短辺の長さの 1/2 で割った値に一致します。中立面とは、4 つあるエッジの中点すべてを通る平面のことです。各節点はこの平面から同一の距離に位置します。ねじれ角を、中立面の角度に 2 の平方根の 2 倍を乗じた値として計算すれば、小角度で曲げた正方形の曲げ角度とほぼ同じ値が得られます。中立面の角度に乗じる数の因数として 2 が現れるのは、曲げ角度の合計の代わりに中立面の角度を使用したことによるものです。一方 2 の平方根は、対角線の 1/2 の代わりに辺の 1/2 を使用したことによります。
- [節点角]: オンにすると、任意の面の最大の節点角(内部)に基づいて要素が表示されます。
- [アスペクト比]: オンにすると、アスペクト比に基づいて要素が表示されます。
3 角形要素の場合、最も長い辺の長さを、その辺を底辺としたときの3 角形の高さで割った値がアスペクト比です。この比に 3/4 の平方根を乗じたものをアスペクト比とすれば、正 3 角形のアスペクト比が 1.0 になります。
4 辺形要素(プレート要素および 2D 要素)の場合、最も長い辺の長さを、その辺から他の節点までの最大距離で割った値がアスペクト比です。正方形のアスペクト比は 1.0 です。また、縦の長さが 1、横の長さが 2 である矩形のアスペクト比は 2.0 です。
ブリック要素(8 節点)の場合は、向かい合った面が 3 組あるため、各面の中点とその対面の中点とをラインで結ぶことにより、全部で 3 本のラインを描くことができます。これらのラインはブリックの中心で交わるため、その中から任意の 2 本を組み合わせて 1 つの平面が定義されます。2 本のラインにより定義されたそれぞれの平面について、その平面から第 3 のラインの端点までの距離を、その平面を定義する 2 本のラインのうち長い方の長さで割った値が計算できます。これら 3 つの値のうち最も大きいものが、ブリックのアスペクト比になります。矩形ソリッドの場合は、4 辺形である各面のアスペクト比の中で最も大きな値が、そのアスペクト比となります。
ウエッジ要素(6 節点ブリック)の場合、ウエッジの 2 つの 3 角形面をつなぐエッジの中点を結ぶことにより、内部に 3 角形を描くことができます。この3 角形の最も長い辺の長さを b、高さを h、3 角形面の中心点どうしを結ぶラインの長さを hw とするとき、sqrt(3)*h/(2*b)、hw/b、および b/hw の中の最大値がアスペクト比になります。正 3 角形をその辺の長さと同じ距離だけ押し出して作成したウエッジ要素のアスペクト比は 1.0 です。
ピラミッド要素(5 節点ブリック)の場合、h は 4 辺形の中立面の上の点の高さとします。4 辺形の最も長い辺の長さを b とするとき、4 辺形のアスペクト比、h/b、および b/h の中の最大値がアスペクト比になります。
4 面体要素(4 節点ブリック)の場合、底面の 3 角形の面積を ai、高さを hi とし、4 つある底面のそれぞれについて、それらの値を求めます。このとき、4 つの底面に関する Cf * hi/sqrt(ai) および sqrt(ai)/(Cf * hi)の中の最大値がアスペクト比になります。Cf が (3/4)^3/4 の場合、正 4 面体のアスペクト比は 1.0 です。
- [長さ/短さ比]: オンにすると、長短比に基づいて要素が表示されます。長さ/短さ比とは、最も長いエッジの長さを最も短いエッジの長さで割った値のことです。
- [面積/体積比]: オンにすると、面積を体積で割った値に基づいてソリッド要素が表示されます。厳密に言うと、面積/体積比は、面積の 1/6 の平方根を体積の立法根で割った値として定義されます。立方体の面積/体積比は 1.0 です。また、平坦な要素(プレート)の面積/体積比も 1.0 です。
- [プレートの厚さ]: このコマンドは、プレート要素またはシェル要素に対してのみ使用できます。コンターは、これらの要素の厚さによって異なります。
- [4 面体のつぶれ度]: このコマンドは、4 節点 4 面体要素を含むブリック モデルに対して使用できます。このコマンドを選択すると、4 面体要素が、その最も長いエッジの長さと最も短いエッジの長さとの比(L/h)に基づいて表示されます。それ以外のタイプの要素はシェーディングされません。 ヒント: 内部の要素を確認するには完全なメッシュを表示する必要があるにもかかわらず、4 面体要素の数は通常その他のタイプの要素よりも少ないため、シェーディングされていないその他すべての要素を除外して結果を表示することは困難な場合があります。[フィルタモジュール]を使用すると、シェーディングされた要素のみ選択し、選択されていない要素は非表示にすることができます。
- [要素の長さ]: オンにすると、ライン要素(ビーム要素、トラス要素など)がその長さに基づいて表示されます。それ以外のタイプの要素はシェーディングされません。