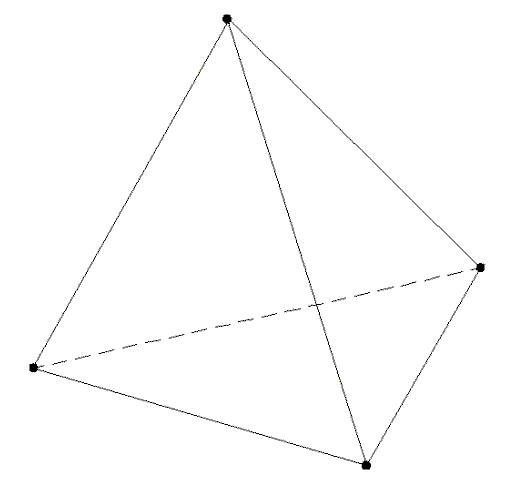
4 面体要素には、4 節点または 10 節点のアイソパラメトリックと湾曲構造のサブパラメトリック 4 面体があります。図 1 は標準的な要素を示したものです。図 2 は 4 面体要素の例を示しています。
図 1: 標準的な 4 面体要素
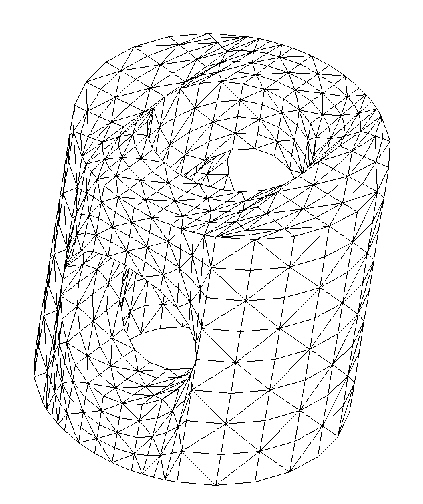
図 2: 4 面体要素の代表的な応用例
4 面体要素のサーフェス番号の決定
4 面体要素のサーフェス番号に荷重を適用する場合、一部のモデルは同一サーフェス番号にロードされるサーフェス上のラインが足りないことがあります。この状態では次のような現象が起こります。CAD ソリッド モデルから作成されたモデルの場合、その CAD モデルのサーフェスと一致する面はすべて、線のサーフェス番号にかかわらず荷重を受けます。自作モデルのパーツと CAD パーツとの関連付けが外れるように変更された自作モデルと CAD パーツ上では、サーフェスを定義する 3 本のラインのうち 2 本が共通であるサーフェス番号により、要素面のサーフェス番号が決定されます。
4 面体要素のパラメータ
最初に、[要素定義]ダイアログの[材料モデル]リスト ボックスで、このパーツに適用する材料モデルを指定します。利用可能な材料モデルは次のように分類されます。各材料モデルの詳細については、「材料特性」の該当ページを参照してください。
-
弾性
- [等方性]: この材料モデル オプションは、応力-ひずみ曲線の弾性域内のみでたわみが生じるパーツに使用します。この材料モデルを使用する場合、パーツでは、すべての方向で同一の材料特性が設定されている必要があります。単一のヤング率およびポアソン比が必須の材料特性となります。
- [直交異方性]: この材料モデル オプションは、応力/ひずみ曲線の弾性領域のみでたわみが生じるパーツに対して使用します。パーツでは、一定の方向に異なる材料特性を設定することができます。特に、直交座標系における直交する 3 方向のうち 1 つまたは 2 つの方向の材料特性が異なることがあります。
- [曲線]: この材料モデル オプションは、地質材料の解析でも使用できます。このモデルでは、現在の体積ひずみの区分線形関数によって、瞬間的な体積弾性率およびせん断弾性率が定義されます。
- [熱弾性]: この材料モデルは、応力-ひずみ曲線の弾性域内のみでたわみが生じる一方で、温度差による応力も生じる可能性がある材料をモデル化する際に使用します。
- [温度依存の直交異方性]: この材料モデルは、方向だけでなく温度によっても材料特性が異なるパーツに使用します。特に、直交座標系における直交する 3 方向のうち 1 つまたは 2 つの方向の材料特性が異なることがあります。材料特性は複数の温度で指定します。値は、2 つの温度値間で線形補間されます。材料特性を定義する温度範囲には、予想温度を含める必要があります。
- [ダンカン-Chang 土壌モデル]: Duncan-Chang (1970) モデルは、地盤をシミュレーションする際に使用します。このモデルは土の3 軸試験を基にしており、応力-ひずみ関係を双曲線で表します。この材料モデルを使用する場合は、[高度]タブの[解析定式化]を[非線形材料に限る]に設定します。
- [Moldflow]: パーツが射出成形される場合、成形工程に起因する異方性材料特性は、Autodesk Moldflow のシミュレーションにより得られます。材料モデルとして[Moldflow]を選択します。詳細については、Autodesk® Simulation Moldflow® との相互運用性を参照してください。
-
超弾性
ヒント: 超弾性材料やフォーム材料の積分オーダ([高度]タブで設定)を上げると、パーツに大変形が生じたときの収束に効果があります。
- [Mooney-Rivlin]: この材料モデルは、ゴムなどの超弾性材料をモデル化する際に使用します。
- [Arruda-Boyce]: この材料モデルは、ゴム材料のモデル化に使用する超弾性材料モデルです。この実装は、体積保存変形モードに対する Ogden 材料の作用に従います。
- [Ogden]: この材料モデルは、ゴムなどの超弾性材料をモデル化する際に使用します。
- [Yeoh]: この材料モデルは、ゴムのようなほぼ非圧縮性(体積保存)の超弾性材料をモデル化する際に使用します。解析の定式化として使用できるのは、Total Lagrange 法のみです。
- [Neo-Hookean]: この材料モデルは、ゴムのようなほぼ非圧縮性(体積保存)の超弾性材料をモデル化する際に使用します。解析の定式化として使用できるのは、Total Lagrange 法のみです。
- [Van der Waals]: この材料モデルは、ゴムのようなほぼ非圧縮性(体積保存)の超弾性材料をモデル化する際に使用します。解析の定式化として使用できるのは、Total Lagrange 法のみです。
-
[フォーム材]
- [Blatz-Ko]: この材料モデルでは、体積弾性率のように、体積パーツと非体積パーツとの強力な結合が発生します。その他の超弾性材料モデルと同様、個別に決定できません。
- [Hyperfoam]: この材料モデルは、Ogden 材料モデルに類似した超弾性材料に使用します。この材料モデルは、材料の圧縮率を考慮します。平面ひずみ要素には適用できません。
-
粘弾性
- [粘弾性 Arruda-Boyce]: Arruda-Boyce (超弾性)材料モデルを粘弾性に応用したものです。
- [粘弾性 Blatz-Ko]: Blatz-Ko (ハイパーフォーム)材料モデルを粘弾性に応用したものです。
- [熱クリープ粘弾性]: この材料モデルは、[熱弾性]: この材料モデルは、応力-ひずみ曲線の弾性域内のみでたわみが生じる一方で、クリープも生じる可能性がある材料をモデル化する際に使用します。クリープは、経時的に一定の荷重を受けてモデルがたわむときに発生します。この材料モデルで使用するクリープ則の設定については、「 4 面体要素の熱特性を定義する」の項を参照してください。
- [粘弾性 Ogden]:Ogden (超弾性)材料モデルの粘弾性版。
- [粘弾性 Hyperfoam]: ハイパーフォーム材料モデルを粘弾性に応用したものです。
- [線形粘弾性等方体]: 材料が弾性ソリッドおよび粘性流体の特性を示す粘弾性材料モデルです。粘弾性特性は Prony 級数に基づきます。この特性はすべての方向で等しく(等方性)、温度に依存しません。
- [線形粘弾性直交異方性]: 材料が弾性ソリッドおよび粘性流体の特性を示す粘弾性材料モデルです。粘弾性特性は Prony 級数に基づきます。この特性は 3 つの垂直方向で異なり(直交異方性)、温度に依存しません。
- [線形熱粘弾性等方体]: 材料が弾性ソリッドおよび粘性流体の特性を示す粘弾性材料モデルです。粘弾性特性は Prony 級数に基づきます。この特性はすべての方向で等しく(等方性)、温度に依存します。
- [線形熱粘弾性直交異方性]: 材料が弾性ソリッドおよび粘性流体の特性を示す粘弾性材料モデルです。粘弾性特性は Prony 級数に基づきます。この特性は 3 つの垂直方向で異なり(直交異方性)、温度に依存します。
- [粘弾性 Mooney-Rivlin]: Mooney-Rivlin (超弾性)材料モデルを粘弾性に応用したものです。
- [粘弾性 Neo-Hookean]: Neo-Hookean (超弾性)材料モデルを有限ひずみの粘弾性に応用したものです。
- [粘弾性 Yeoh]: Yeoh (超弾性)材料モデルを有限ひずみの粘弾性に応用したものです。
- [粘弾性 Van der Waals]: Van der Waals (超弾性)材料モデルを有限ひずみの粘弾性に応用したものです。
-
[塑性]
- [Hardening 等方硬化をともなうフォン ミーゼス]: この材料モデル オプションは、解析中に塑性変形が発生する可能性があるパーツで使用します。双線形曲線を使用して応力-ひずみ関係を表します。
- [移動硬化によるフォン ミーゼス]: この材料モデル オプションは、解析中に塑性変形を示すパーツに使用します。双線形曲線を使用して応力-ひずみ関係を表します。モデルで循環荷重が発生する場合は、[Hardening 等方硬化をともなうフォン ミーゼス]材料モデル オプションに対してこの材料モデル オプションの使用を優先します。
- [Hardening 等方硬化をともなうフォン ミーゼス曲線]: この材料モデル オプションは、解析中に塑性変形が発生する可能性があるパーツで使用します。応力-ひずみ関係を表すために、複数のデータ ポイントを持つ応力-ひずみ曲線を指定できます。
- [移動硬化によるフォン ミーゼス曲線]: この材料モデル オプションは、解析中に塑性変形を示すパーツに使用します。応力-ひずみ関係を表すために、複数のデータ ポイントを持つ応力-ひずみ曲線を指定できます。モデルで循環荷重(Bauschinger 効果)が発生する場合は、[Hardening 等方硬化をともなうフォン ミーゼス]材料モデル オプションに対してこの材料モデル オプションの使用を優先します。
- [熱塑性]: この材料モデルは、解析中に塑性変形を示し、かつ温度差による応力を示す可能性がある材料をモデル化する際に使用します。
-
粘塑性
- [熱クリープ粘塑性]: この材料モデルは、塑性変形を示し、かつクリープも示す可能性がある材料をモデル化する際に使用します。クリープは、経時的に一定の荷重を受けてモデルがたわむときに発生します。この材料モデルで使用するクリープ則の設定については、「 4 面体要素の熱特性を定義する」の項を参照してください。
- [Drucker-Prager]: この材料モデルはフォン ミーゼス材料モデルに似ていますが、降伏関数が追加されています。このモデルでは、体積ひずみにより降伏関数が変化するものとみなします。この現象はコンクリートや岩などの材料で発生します。
-
コンクリート
- [鉄筋コンクリート]: この材料モデルでは、さまざまな引張挙動や圧縮挙動に対応できます。比較的単調な荷重下でのコンクリートの亀裂や圧壊をシミュレーションできます。亀裂や圧壊は、巨視的亀裂を個別に追跡するのではなく、複数の積分点での弾性変性によってシミュレーションされます。コンクリート材料には、最大 3 方向の鉄筋を使用できます。ただし、鉄筋の位置(高さまたは奥行き)の詳細は考慮されません。鉄筋は完全付着として処理されます。鉄筋コンクリート材料モデルを使用する場合は、[高度]タブの[解析定式化]を[非線形材料に限る]に設定します。
-
電気
- [圧電]: この材料モデルは、電圧差により生じる応力を示すパーツに対して使用します。弾性特性と圧電特性の両方を指定する必要があります。
- [一般圧電]: この材料モデルは、[圧電]材料モデルから一般化した形式です。弾性剛性マトリックスおよび圧電性マトリックスの係数を指定する必要があります。
このパーツの 4 面体要素にアクティブな中間節点を追加する場合、[中間節点]ドロップダウン ボックスの[含む]オプションを選択します。このオプションを選択した場合、4 面体要素に各エッジの中点で定義した節点が追加されます。(CAD ソリッド モデルのメッシュでは、中間節点は、メッシュ作成前に選択したオプションに応じて、CAD サーフェスのオリジナルの曲率に従います。変更される自作のモデルおよび CAD モデルでは、中間節点はコーナー節点間の中間に置かれます。)これにより、4 節点 4 面体要素が 10 節点 4 面体要素に変わります。中間節点を伴う要素は、より正確に計算された勾配となります。この効果は、屈曲した平面での複数要素の曲げ挙動をモデル化しようとする場合に特に有効です。中間節点を持つ要素は処理時間が増大します。メッシュが十分に小さい場合は、中間節点を追加しても正確度がそれほど向上しないこともあります。
[解析タイプ]ドロップダウンを使用して、目的とする変位のタイプを設定します。[微小変形]は、運動がなく、小さなひずみしか受けないパーツに適しています。この場合、大きな変形の結果生じた非線形の幾何学的影響は無視されます (これにより、[高度]タブの[解析の定式化]が[非線形材料に限る]に設定されます) 。[大変形]は、運動や大きなひずみを受けるパーツに適しています ([高度]タブの[解析定式化]を、解析に必要な設定にすることも必要です。)
- 中間節点における変位は常に出力されます。中間節点における応力とひずみは、ユーザにより解析の実行前にこれらの結果を出力するオプションがアクティブにされている場合にのみ出力されます。このオプションは、[出力]タブの[設定]
 [モデル設定]
[モデル設定]  [パラメータ]
[パラメータ]  [高度]ダイアログにあります。(詳細については、「解析の設定と実行」>「非線形」>「解析パラメータ」>「高度な設定」>「出力ファイルを制御する」を参照してください。)
[高度]ダイアログにあります。(詳細については、「解析の設定と実行」>「非線形」>「解析パラメータ」>「高度な設定」>「出力ファイルを制御する」を参照してください。) 
 [オプション]
[オプション] [解析]タブにある[非線形解析のための既定として大変形を使用]オプションを使用して、[解析タイプ]の既定値を小変形にするか大変形にするかを設定します。
[解析]タブにある[非線形解析のための既定として大変形を使用]オプションを使用して、[解析タイプ]の既定値を小変形にするか大変形にするかを設定します。
4 面体要素の熱特性を定義する
[熱]領域:
4 面体要素のパーツで熱効果を含む材料モデルを使用する場合、[要素定義]ダイアログの[熱]タブの[応力なしの参照温度]フィールドで値を指定する必要があります。この値は、熱成長の定数に関連付けられる要素ベースの荷重を、節点温度の双線形補間を用いて計算するための参照温度として使用されます。
[クリープ]領域
4 面体要素のパーツでクリープを含む材料モデルを使用する場合、[クリープ則]ドロップダウン ボックスでオプションを選択します。この設定は、解析中のクリープ効果の計算に使用されます。使用可能なクリープ則は次のとおりです。
- [クリープなし]: このオプションを選択すると、解析にクリープ効果は追加されません。
- [べき乗則]: このオプションは、単軸クリープ則とも呼ばれます。この式は、
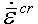 = C
1
x
= C
1
x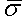 C2
x t
C3
で表されます。
C2
x t
C3
で表されます。 - [Garofalo]: このオプションは、双曲線正弦クリープ則とも呼ばれます。この式は、
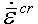 = A
0
x [sinh(A
1
x
= A
0
x [sinh(A
1
x 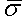 )]
A2
で表されます。
)]
A2
で表されます。 - [二重べき乗則]: このオプションはべき乗則と似ていますが、高応力レベルでの実験結果に近い結果を出すための項が追加されています。この式は、
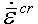 = C
1
x
= C
1
x 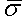 C
2
x t
C3
+ C
4
x
C
2
x t
C3
+ C
4
x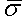 C5
x t
C6
で表されます。
C5
x t
C6
で表されます。
ただし、![]() は有効クリープひずみ速度、
は有効クリープひずみ速度、![]() は有効応力です。材料特性の入力に関する重要な情報については、「解析の設定と実行」>「非線形」>「材料特性」>「熱クリープ粘弾性」を参照してください。
は有効応力です。材料特性の入力に関する重要な情報については、「解析の設定と実行」>「非線形」>「材料特性」>「熱クリープ粘弾性」を参照してください。
均一の大きさに分割された時間ステップでクリープ計算が行われるようにする場合は、[時間積分法]ドロップダウン ボックスで[固定サブステップ]オプションを選択します。不定の大きさに分割された時間ステップでクリープ計算が行われるようにする場合は、[可変サブステップ]オプションを選択します。この 2 つの方法は時間硬化則に基づいており、陽的時間積分法が使用されます。これらの方法は、一部の荷重条件では不安定になる場合があります。熱粘弾性クリープ材料モデルで[クリープひずみの定義]ドロップダウン ボックスを使用する場合、[時間積分法]ドロップダウン ボックスに[α-法]オプションが追加され、このオプションを使用できるようになります。この方法では、クリープ挙動を改善するために陰的時間積分法が使用されます。この方法は無条件に安定します。
[応力なしの参照温度]フィールドでは、熱応力が存在しない温度を指定します。
非循環荷重を適用して解析を実行する場合は、[クリープひずみの定義]ドロップダウン ボックスの[有効な]オプションを選択します。周期的な荷重を伴う解析を実行する場合、[修正された]オプションを選択します。
解析中、クリープ計算は各時間ステップのサブステップでの反復として実行されます。1 つの時間ステップで使用できるサブステップの数を、[サブステップの最大数]フィールドで指定できます。また、1 つのサブステップで実行できる反復の数を、[サブステップにおける反復の最大数]フィールドで指定できます。サブステップで反復が 1 回実行されるごとに、クリープ応力とクリープひずみがその前回の反復に対して比較されます。この値が、[クリープひずみ計算の許容誤差]と[クリープ応力計算の許容誤差]の各フィールドに指定した許容誤差の範囲にない場合は、もう一度反復を実行する必要があります。
時間積分法として[α法]を使用するときは、[時間積分パラメータ]を指定する必要があります。時間積分法に完全陽解法を使用する場合は(ただし、固定/可変サブステップの陽解法とは異なる)、[時間積分パラメータ]フィールドに 0.0 と入力します。完全陰解法を使用する場合は、[時間積分パラメータ]フィールドに 1.0 と入力します。時間積分パラメータが 0.5 より大きいときは、この方法は無条件に安定します。
4 面体要素の方向を制御する
4 面体要素のこのパーツで直交性材料モデルを使用する場合、[要素定義]ダイアログの[直交異方性]タブ、材料軸 1~3 の方向を定義する必要があります。基本的には次の 2 種類の方法で定義できます。
方法 1:
最初の方法では、全体軸のいずれかを材料軸 1 として選択します。[次を使用した材料軸方向]ドロップダウン ボックスで[全体 X-方向]オプションを選択した場合、直交する各材料軸と X 軸、Y 軸、Z 軸の対応関係は次のようになります。
- 材料軸 1: X 軸
- 材料軸 2: Y 軸
- 材料軸 3: Z 軸
[グローバルなY-方向]オプション([材料軸方向指定]でドロップダウン ボックスを使用して設定)を選択する場合、材料軸の方向は、次のように X 軸、Y 軸、Z 軸に従います。
- 材料軸 1: Y 軸
- 材料軸 2: Z 軸
- 材料軸 3: X 軸
[グローバルなZ-方向]オプション([材料軸方向指定]でドロップダウン ボックスを使用して設定)を選択する場合、材料軸の方向は、次のように X 軸、Y 軸、Z 軸に従います。
- 材料軸 1: Z 軸
- 材料軸 2: X 軸
- 材料軸 3: Y 軸
1 つ目の方法では、[材料軸回転角]フィールドに角度を入力することによって、選択した全体軸の回りに軸を回転することができます。この角度は、右手の法則に従います。
方法 2:
2 番目の方法では、[次を使用した材料軸方向]ドロップダウン メニューで[空間点]オプションを選択します。次に、3 つの空間点の座標を[空間点の座標]テーブルで定義する必要があります。空間点の適切なインデックスを[空間点 1 のインデックス]、[空間点 2 のインデックス]、[空間点 3 のインデックス]ドロップダウン メニューで選択します。
- 材料軸 1 は、[空間点 1 のインデックス]ドロップダウン メニューの空間点から[空間点 2 のインデックス]ドロップダウン メニューの空間点までのベクトルです。
- 材料軸 2 は、局部座標軸 1 に対して垂直で、3 つの空間点から形成される平面にあり、軸 1 で [空間点 3 のインデックス] ドロップダウン メニューの空間点と同じ側にあります。
- 材料軸 3 は、材料軸 1 および 2 のクロス積として計算されます。
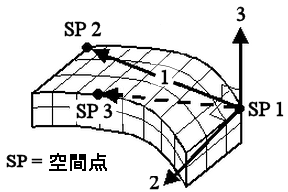
図3: 材料軸の方向
4 面体の詳細パラメータ
解析定式化: 4 面体要素に使用する定式化の方法を[高度]タブの[解析定式化]ドロップダウン ボックスで選択します。
- [非線形材料に限る]オプションが選択されている場合、非線形材料モデルの効果は加味されますが、計算はすべて未変形のジオメトリに基づいて実行されます。したがって、この定式化は、小さなひずみを受け、運動がないパーツに適しています。これは、[一般]タブの[解析タイプ]が[微小変形]に設定されている場合、使用可能な唯一のオプションです。
- [Total Lagrange 法]オプションを選択すると、すべての静的変数および運動学変数について、初期状態で変形されていないモデルの構成が参照されます。この定式化は、運動と小さなひずみを受けるパーツに適しています。材料特性は、エンジニアリングにおける応力およびひずみである点に注意が必要です。
- [Updated Lagrangian 法]では、すべての静的変数および運動学的変数に対して、モデルの最後に計算された形状が参照されます。 この定式化は、運動と大きななひずみを受けるパーツに適しています。材料特性は、真応力および真ひずみの観点から考える必要があります。
[応力更新法]:
[応力更新法]は、材料モデル([一般]タブ)を次のいずれかの塑性材料モデルに設定する場合に使用します。
- [等方硬化をともなうフォン ミーゼス]
- 移動硬化によるフォン ミーゼス
- [等方硬化をともなうフォン ミーゼス曲線]
- [等方硬化をともなうフォン ミーゼス曲線]
この設定により、材料が塑性を示すときの構成方程式(応力/ひずみ則)を積分するための数値アルゴリズムを指定できます。[応力更新方法]で使用可能なオプションは次のとおりです。
- [陽解法]: (独自手法)。 このオプションでは、構成方程式の積分に陽的サブ増分前進オイラー法を使用します。[陽解法]オプションは、実行時間が短いので単純引張などの単純な問題に最適です。ただし、荷重、時間ステップ サイズ、および材料の応力-ひずみ曲線の複雑性の影響を受けやすい方法でもあります。
- [一般化された中点法]: このオプションでは、構成方程式の積分に陰解法を使用します。この方法では累積誤差が減少し、応力更新プロセスが無条件に安定します。このため、接触の問題、極度の塑性、材料の複雑な応力-ひずみ曲線など、複雑な解析により適しています。
応力更新法に関するガイドライン:
- 解析結果が妥当である(予測された挙動に沿っている)ことを確認します。たとえば、ジオメトリ、荷重、および境界条件に対称性がある場合、異方性材料を除き、対称の解析結果が予測されます。解析結果が直観に反していたり、解に不連続または不安定性がある場合は、[応力更新法]を変更するか、次のガイドラインで説明するように変数の更新頻度を増加します。
- [陽解法]を選択するか、[一般化された中点法]を選択するかにかかわらず、応力変数とひずみ変数の更新頻度を高くすると、塑性材料モデルの解析精度が向上します。更新頻度を増加するには、次のいずれかの方法を実行します。
- [解析パラメータ]ダイアログ ボックスで、時間ステップ サイズを減少します(キャプチャ レートを増加します)。
- [解析パラメータ - 高度]ダイアログ ボックスの[平衡]タブの[非線形反復解析法]で、[自動]または[結合されたニュートン]ではなく[完全ニュートン法]を選択します。
- [一般化された中点法]は、一般的に[陽解法]よりも大きな時間ステップを許容できます。また、より高精度の解析結果が得られます。ただし、計算負荷が高くなり、解析時間が長くなります。
- 背景: メカニカル イベント シミュレーション(MES)では、構成関係を積分して未知の応力増分を取得することが非常に重要となります。これらの関係は、一連の常微分方程式を定義します。通常、これらの積分法は陽解法と陰解法に分類されます。陽解法は前方解析のみを実行します。つまり、増分の初期段階における材料の応力-ひずみ曲線の勾配を選択して、この勾配を基に増分の最後における応力を計算します。陰解法の場合、ソルバーは前方解析と後方解析の両方を実行し、複数の反復を使用して勾配を計算する必要があります。応力-ひずみ曲線の勾配でひずみの増分を乗算して、応力を特定します。
[陽解法]による積分法では、降伏曲面、塑性ポテンシャル勾配、および硬化則はすべて既知の応力状態で評価されます。最終的な応力の予測に特定の反復は厳密には必要ありません。
[一般化された中点法]による積分法(陰解法の一種)では、この条件が積分で強制されないため、単純な反復調整により次の増分の応力および硬化パラメータは降伏曲面に復元されます。この補正では、非線形方程式の解を反復的に得るために追加の作業が必要となります。一方、陽解法の場合、ガウス点ごとの応力を計算するために連立非線形方程式の解は必要ありません。
[一般化中間点のためのパラメータ]は、[応力更新法]を[一般化された中点法]に設定したときに入力します。0 以上 1 以下の範囲で入力することができます。パラメータを 0 (ゼロ)に設定した場合、完全陽解法のいずれかのアルゴリズムが得られます([応力更新方法]で[陽解法]オプションに設定した場合と同じ)。ただし、解法は無条件に安定ではありません。パラメータを 0.5 以上に設定した場合、解法は無条件に安定します。パラメータを 0.5 に設定した場合の解法は中間点アルゴリズムとして知られています。1 に設定した場合の解法は完全後退オイラー法または最接近点アルゴリズムとして知られており、完全陰解法です。値 を 1 にしたときが最も正確で、時間ステップが大きい場合は特に有効です。
[ひずみ測定]:
[ひずみ測定]は、[材料モデル]([一般]タブ)を[等方性]に設定し、[解析定式化]を[Updated Lagrangian 法]に設定した場合に使用します。この設定を使用すると、Updated Lagrange 法の収束が改善されます。[ひずみ測定]では、次のオプションが使用可能です。
- [Almansiのひずみ]: (元来の方法)このオプションでは、構成関係に Cauchy 応力と Almansi のひずみを使用します。小ひずみの問題にのみ使用できます。
- [対数ひずみ]: このオプションでは、構成関係に Cauchy 応力と仮想対数ひずみ(増分ひずみ)を使用します。大ひずみを含め、すべての問題に使用できます。これは亜弾性モデルであり、圧縮性材料よりも非圧縮性材料(ポアソン比が 0.5)に適しているという難点があります。これは、弾性率が実際には体積変化に伴い変化するところを、一定であると仮定されるためです。
[要素の重なり]:
[要素の重なりを許容]チェック ボックスをアクティブにすると、ラインが要素に解読される場合に重なる要素を作成できるようになります。要素をモデル化する際に重なりが必要となることがあります。特に、平面運動に制限される問題に当てはまります。
[出力オプション]:
解析中、各要素に対する応力の結果を時間ステップごとにテキストのログ ファイルへ書き込むようにする場合は、[力とモーメントの詳細出力]チェック ボックスをオンにします。その場合、出力データの量が大きくなる場合があります。
フォン ミーゼス材料モデルのいずれかを選択した場合、現在の材料の状態(弾性または塑性)、現在の降伏応力制限、現在の等価応力制限および角の節点の等価塑性ひずみ出力、および/または各時間ステップの統合ポイントを含むよう選択できます。[追加の出力]ドロップダウン ボックスで該当するオプションを選択して設定します。
[選択型低減積分(平均膨張)]:
物理的問題の多くは、原則的に体積を保存する運動が関係しています。このように挙動する材料を、非圧縮性材料と呼びます。たとえば、剛塑性流れを生じるゴムや金属は、ほぼ非圧縮性です。[選択型低減積分(平均膨張)]チェックボックスをオンにすると、非圧縮性の限界と高圧縮性体積変化を表す通常の圧縮性 FEA 定式化に変更が加えられます。この方法(B-Bar)によって、体積の固定を回避することができます。
このチェックボックスをオフにした場合は、変位のダイラタンシー成分(体積に関連)が、偏差成分と同じ次数で積分されます。オンにした場合は、平均値を使ってダイラタンシーの寄与が計算されます。
このオプションが解析に役立つ例を 2 つ紹介します。
- 材料特性: 等方性線形弾性で、非圧縮性の条件をポアソン比で表すことができます。ポアソン比が 0.5 に近付くと、せん断に対する抵抗が変化しないと仮定して、体積変化に対する抵抗が大幅に増加します。つまり、体積弾性率が無限大に近付きます。
- 材料モデルと変形: 弾塑性材料モデルでは、塑性変形が弾性変形よりも大きく、力学理論では塑性変形には体積変化がないものとみなします。したがって、材料は実質的に体積が一定となります。他の非線形材料モデルでも、同様の仮定が存在します。
[選択型低減積分(平均膨張)]チェックボックスをオンにするためには、[適合性]を[強制的]に設定する必要があります。
圧電性材料のオプション:
部品に対して圧電性材料モデルの 1 つが選択されている場合、[要素定義]ダイアログ ボックスの[高度]タブにおいて、2 つの追加オプションが使用可能になります。
- [節点電圧荷重曲線]入力フィールドを使用して、すべての節点電圧をコントロールするために解析イベント全体をとおして使用される、荷重曲線の数を指定します。
- 複数の圧電性材料にわたって適用される電圧の差異により、圧電性の部品が微小変形する原因となる、電場が生じます。ひずみの量は通常小さくなります。部品の変形の電場での影響は小さく、このため結果の圧電性変形に対する影響は非常に小さくなります。この影響を考慮に入れる場合は、[電場を更新]チェック ボックスを有効にします。そうしない場合、電場は部品の初期(変位がない)条件に基づいた形になります。
土壌条件を定義する
Duncan-Chang 材料モデルを選択した場合は、[土]タブが有効になります。解析に応じて次のオプションを設定します。ここでの入力は、土壌の初期状態関係します。詳細については、「解析の設定と実行」>「非線形」>「材料特性」>「Duncan-Chang 材料特性」>「Duncan-Chang の論理的説明」も参照してください。
- [静水圧を付加]: このオプションをオンにすると、入力フィールドに設定した一定の静水圧に基づき初期応力が作成されます。(この場合の静水圧はすべての方向に等しく作用します。深さの増加に伴い増大する水圧と混同しないでください。)圧力の大きさは 0 (ゼロ)より大きくする必要があります。
- [自身の重量を付加]: このオプションをオンにすると、モデル化された土壌の重量に基づき初期応力が作成されます。
- [サーフェスの基準点]: X、Y、Z 座標を指定します。これにより、土壌の重量による圧力がゼロになる位置が決まります。モデルが地下深くの土の断面である場合、 基準点はモデル化したパーツの上に設定できます。
- [側面土圧の係数]: ほとんどの土壌では、真の(すべての方向に大きさが等しい)静水圧は発生しません。水平方向の応力は、通常、垂直方向の応力の一部しかありません。横応力と垂直応力との比率によって側面土圧の係数が決まります。入力値は 0 ~ 1 の範囲で指定する必要があります。
- [重力加速度]: 自身の重量による応力分布を作成するには、重力定数、および応力分布が発生するために作用する重力の方向を入力します。この方向は、通常、解析での重力の方向と同じです。ただし、初期応力が作成された時点やモデルの現在の方向とは別の方向に土壌が表されている場合は、別の方向を使用することもできます。この場合、土壌は移動しています。
4 面体要素の使用の基本手順
- 単位系が定義されているようにしてください。
- モデルで使用される解析タイプが非線形になっていることを確認します。
- ブリック要素に設定するパーツの[要素タイプ]列を右クリックします。
- [4 面体]コマンドを選択します。
- [要素定義]の見出しを右クリックします。
- [要素定義を編集]コマンドを選択します。
- [一般]タブの[材料モデル]ドロップダウン ボックスで該当する材料モデルを選択します。
- [材料モデル]ドロップダウン ボックスで[熱塑性]、[熱弾性]、[粘塑性]、または[粘弾性]オプションを選択した場合は、[熱]タブで必要な情報を指定します。
- [OK]ボタンをクリックします。