Pour définir les paramètres d’analyse modale pour les nouveaux cas dynamiques de la structure, effectuez l'une des actions suivantes :
- Sélectionnez un cas d’analyse modale dans la boîte de dialogue Nouveau cas, puis cliquez sur OK.
- Sélectionnez un cas d'analyse modale dans la boîte de dialogue Type d'analyse, puis cliquez sur Définir paramètres.
L'utilisation du solveur itératif est conseillée lors de la résolution des problèmes nécessitant de gros calculs. Le solveur itératif propose trois méthodes de résolution des problèmes aux valeurs propres. Pour ce faire, sélectionnez Solveur itératif dans la boîte de dialogue Préférences de la tâche de la section Analyse de la structure.
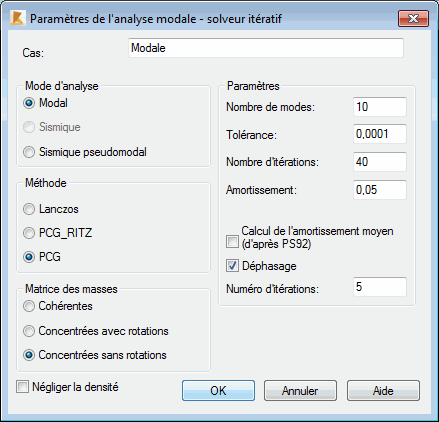
Mode d’analyse
Dans la présente version du solveur itératif, les modes modal et sismique (pseudomodal) sont disponibles. Le mode modal est disponible seulement pour la méthode de gradient conjugué avec l’utilisation de préconditionnement (preconditioned conjugate gradient method - PCG) [1-4]. Le mode sismique (pseudomodal) est disponible pour la méthode de Lanczos modifiée de même que pour la méthode de gradients de Ritz (PCG_Ritz - Ritz gradient method).
Méthode
Méthode de Lanczos
Lanczos est une méthode de Lanczos modifiée permettant d’éviter la factorisation de matrices de taille importante. La méthode de gradient conjugué avec l’utilisation de préconditionnement est utilisée pour la composition de l’ensemble de vecteurs de Lanczos au lieu d’effectuer la résolution inversée (back resolution) de la matrice de rigidité factorisée. Tous les types de préconditionnement définis pour l’analyse statique sont disponibles (Outils > Préférences de la tâche > Méthode itérative > Paramètres).
La méthode de Lanczos modifiée est conseillée pour l'analyse sismique et spectrale de grandes structures lorsque plusieurs modes sont requis.
- Paramètres exigés
Type de matrice des masses (concentrée avec rotations ou cohérente) et nombre de modes.
La précision des calculs dépend du nombre de modes et de la tolérance adoptée pour les calculs des vecteurs de Lanczos (la tolérance est affectée dans la boîte de dialogue affichée après la sélection de la commande Outils/Préférences de la tâche/Analyse de la structure/Méthode ltérative/Paramètres, la tolérance est la même que pour les cas statiques). Dans la boîte de dialogue Paramètres de l’Analyse Modale – Solveur itératif, la tolérance signifie la tolérance de la résolution du problème aux valeurs propres général comprenant les vecteurs de Lanczos définis, la tolérance en question ne peut pas être inférieure à 1.0e-04.
Plus le nombre de modes pris en considération est élevé, plus les petits vecteurs de Ritz seront proches des valeurs correspondantes. La somme des masses modale sera plus précise.
PCG_Ritz
PCG_Ritz est la méthode de Ritz selon laquelle l’approche gradient conjugué avec l’utilisation de préconditionnement est utilisée pour générer l’ensemble de vecteurs de base (méthode de gradient de Ritz [5]). L’utilisation de la méthode PCG_Ritz est conseillée pour une définition approximative rapide des couples propres lors de l’analyse sismique et spectrale. La sélection de la méthode multiniveau est exigée. Il est conseillé d’affecter un niveau d’agrégation. La méthode en question sera efficace pour les problèmes de taille moyenne (jusqu'à 60 000 équations). Tous les types de préconditionnement définis pour l’analyse statique sont disponibles (Outils > Préférences de la tâche > Méthode itérative > Paramètres).
- Paramètres exigés
Type de matrice des masses (concentrée avec rotations ou cohérente) et nombre de modes. La précision des calculs dépend du nombre de modes.
PCG
PCG est une méthode de gradient conjugué avec l’utilisation de préconditionnement [1-5]. Elle est conseillée si un nombre réduit de modes propres est défini. Par exemple, la méthode PCG peut être très utile lors de l’affectation des charges de vent ou lors de la vérification d’une nombre peu élevé de modes propres peu importants obtenus par le biais de la méthode PCG_Ritz. Tous les types de préconditionnement définis pour l’analyse statique sont disponibles (Outils > Préférences de la tâche > Méthode itérative > Paramètres). Tous les types de matrices de masses peuvent être utilisés (matrice de masses cohérentes, concentrées avec rotations, concentrées sans rotations).
- Paramètres exigés :
Nombre de modes ; Tolérance - paramètres de précision relatifs à l'arrêt de l'itération ; Nombre d'itérations - nombre maximal d'itérations autorisé pour chaque mode (le processus d'itération pour chaque mode est arrêté si un paramètre de tolérance actuel est inférieur à la Tolérance ou si le nombre d'itérations actuel dépasse le Nombre d'itérations) ; Décalage - tire parti de la technique de décalage pour accélérer la convergence ; Nombre de répétitions - détermine le nombre de répétitions (pour chaque mode, l'algorithme effectue des itérations en fonction du Nombre d'itérations, corrige une valeur de décalage et répète les itérations en fonction du Nombre d'itérations, du nombre de fois défini par le Nombre de répétitions).
- Paramètres recommandés :
Méthode multiniveau ou sans multiniveau avec approche ICCF (Outils > Préférences de la tâche > Méthode itérative >Paramètres); nModes £ 5; tolérance = 0,01; nombre d'itérations = 100 pour la méthode sans multiniveau ; Décalage - désactivé
- Type de matrice de masses
- Paramètres (nombre de modes, tolérance, nombre d’itérations, amortissement)
- Décalage (accompagné du nombre d’itérations).
Eviter une définition incorrecte des paramètres de solveur itératif
Dans le logiciel, un système de contrôle a été implémenté, qui permet d’éviter une définition incorrecte des paramètres de l’analyse modale pour le solveur itératif. Il est activé lorsque vous cliquez sur OK pour lancer l'analyse modale. Le logiciel affiche un message sur les paramètres de l’analyse. Un clic sur le bouton Oui valide les valeurs des paramètres définis dans la boîte de dialogue. Dans le cas contraire (après un clic sur le bouton Non), le logiciel retourne à la boîte de dialogue Paramètres de l’analyse modale pour vous permettre de corriger les valeurs des paramètres.
Si le solveur itératif en mode sismique pseudomodal est utilisé dans les calculs :
- Le nombre de niveaux d’agrégation doit être égal à 1 (Préférences de la tâche > Analyse de la structure/Paramètres > Méthode itérative).
- Le nombre de modes saisi dans le champ d’édition doit être au moins trois fois plus grand que le nombre de modes recherchés.
- Vérifiez la convergence de la solution pour le nombre de modes comme indiqué dans le point 2 et pour un nombre de modes deux fois supérieur. Si la convergence ne se produit pas (c’est-à-dire si les valeurs propres pour le nombre de modes initial et le nombre de modes deux fois plus grand sont sensiblement différents), il faut augmenter le nombre de modes. Après avoir obtenu une solution convergente, on peut appliquer le filtrage de modes afin de réduire leur nombre.
De plus, dans le type d’analyse, le paramètre Tolérance n’a pas de signification pratique dans les résultats dynamiques (il peut être ignoré). Si les principes décrits ne sont pas observés, les résultats peuvent être imprécis (l’erreur peut atteindre quelques dizaines pour cent).
Références
- Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrices, J. Comp. Phys., 74: 41 - 60, 1988.
- Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Phys., 81: 53 - 69, 1989.
- Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Meth. Appl. Mech. Eng., 62: 195 - 207, 1987.
- M.Papadrakakis, Solving large - scale problems in mechanics, John Wiley & Sons Ltd., 1993.
- Fialko S., High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis, CAMES, 7: 537-550, 2000.
Rubrique connexe :
Principes adoptés pour l’analyse modale
Paramètres de l’analyse modale avec la prise en compte des efforts statiques
Description de l’analyse modale avec la prise en compte des efforts statiques
Description de la méthode d’itération dans le sous-espace par blocs
Analyse modale - précision des calculs