Ez a gyakorlat bemutatja, hogyan hozhat létre TIN-felületeket, majd hogyan adhat hozzá szintvonal-, törésvonal- és peremvonaladatokat a felülethez.
Amikor létrehoz egy felületet, a felület neve megjelenik a Felületek gyűjteményben az Eszköztár Kereső lapján. Erről a helyről végrehajthat más műveleteket is, például adatokat adhat hozzá vagy szerkesztheti a felületet. Az első létrehozáskor a felület üres, így nem látható a rajzon.
Miután a felülethez adatot rendelünk, a felület láthatóvá válik a rajzon, az ajánlott felületstílusban meghatározott megjelenítési beállításnak megfelelően.
TIN felületek
A TIN-felület háromszögekből áll, amelyek egy háromszög alakú szabálytalan hálózatot alkotnak. A TIN vonal az egyik az azon vonalak közül, amelyek a felületi háromszögelést alkotják.
A TIN vonalak létrehozásához az AutoCAD Civil 3D összeköti a legközelebbi felületpontokat. A TIN vonalak háromszögeket alkotnak. A felületen található bármely pont magassága meghatározható azon háromszög töréspontjainak interpolálásával, amelyen a pontok fekszenek.
TIN-felület megjelenített szintvonalakkal
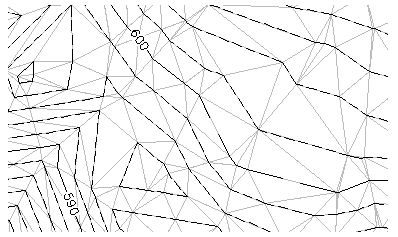
Szintvonaladatok
A szintvonalak a felületmagasság változásainak grafikus ábrázolásai. Felületeket x, y és z koordinátaadatokkal rendelkező 2D vagy 3D vonalláncként megrajzolt szintvonalakból hozhat létre.
Peremvonalak
A peremvonalak olyan zárt vonalláncok, amelyek befolyásolják a vonalláncokon belül, vagy az azokon éppen kívül elhelyezkedő háromszögek láthatóságát. Egy külső peremvonal határozza meg egy felület terjedelmét. A peremvonalon belül található minden háromszög látható, a peremvonalon kívüliek láthatatlanok.
A számítások, mint pl. a teljes terület- és térfogatszámítás, nem foglalják magukba a peremvonalak által elrejtett területeket.
A felületperemek a rajzban található már meglévő sokszögek kiválasztásával határozhatók meg. A felület definíció megjeleníti a számazonosítót és minden peremvonal töréspont listáját.
Felület nem destruktív külső peremvonal hozzáadása előtt

Nem destruktív külső peremvonal hatásai
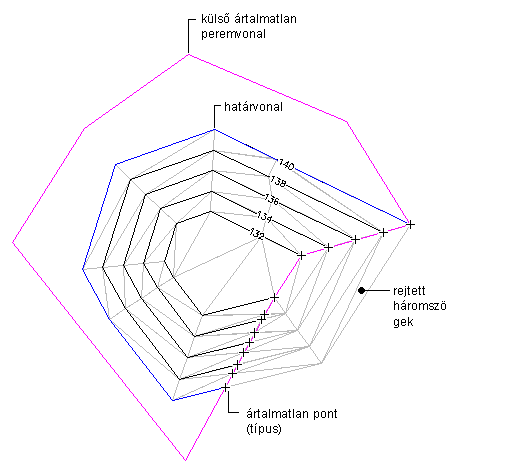
Törésvonalak
A törésvonalak az olyan vonalas felület alakzatokat határozzák meg, mint például támfalak, szegélyek, hosszgerendák teteje és vízfolyások. A törésvonalaknak köszönhetően a felület háromszögelése a törésvonal mentén történik, a háromszögek nem kereszteznek törésvonalat.
A törésvonalak egy pontos felületmodell létrehozásának kulcsfontosságú részét képezik. A törésvonalak azért fontosak, mert a modell alakját nem csupán az adatok önmagukban, hanem azok interpolációja határozza meg.
Törésvonalként 3D vonalakat vagy 3D vonalláncokat alkalmazhat. A vonallánc mindegyik töréspontja TIN-ponttá alakul, ugyanazon XYZ koordinátákkal. 3D-s vonalak esetében minden kiválasztott vonal két-pontos törésvonalként kerül meghatározásra.