Keine
Bei Auswahl dieser Option werden alle Ergebniskonturen aus dem Modell entfernt und die Standardfarben für die Schattierung und die Netzlinien verwendet.
Verschiebung
Durch diese Option wird Farbe auf das Modell angewendet, um die Verschiebung darzustellen. Folgende Befehle stehen zur Verfügung:
- Größe: Legt fest, dass die Anzeige auf der Größe der Verschiebung basieren soll. Dies ist immer ein positiver Wert. Die Größe ist der Abstand, um den der Knoten insgesamt verschoben wurde. mag = sqrt[(dX)^2 + (dY)^2 + (dZ)^2]
- X: Legt fest, dass die Anzeige auf dem Punktprodukt des Verschiebungsvektors mit einem Einheitenvektor in X-Richtung basieren soll. Zeigt die Komponente der Gesamtverschiebung in X-Richtung an.
- Y: Legt fest, dass die Anzeige auf dem Punktprodukt des Verschiebungsvektors mit einem Einheitenvektor in Y-Richtung basieren soll. Zeigt die Komponente der Gesamtverschiebung in Y-Richtung an.
- Z: Legt fest, dass die Anzeige auf dem Punktprodukt des Verschiebungsvektors mit einem Einheitenvektor in Z-Richtung basieren soll. Zeigt die Komponente der Gesamtverschiebung in Z-Richtung an.
- Vektorplot: Legt fest, dass die Anzeige auf der Größe der Verschiebung basieren und das Ergebnis als ein Vektor (Pfeil) an jedem Knoten angezeigt werden soll. Die Länge und Farbe des Pfeils geben die Größe der Verschiebung an, und die Richtung des Pfeils stellt die Vektorrichtung der Verschiebung dar. Unter Anzeigeoptionen: Anzeigeeinstellungen: Vektorenanzeige können sie die Pfeilgrößen anpassen.
Drehung
Durch diese Option wird Farbe auf das Modell angewendet, um die Drehung an jedem Knoten darzustellen. Dieses Ergebnis ist nur für Knoten auf Elementen gültig, die einer Drehung Stand halten. Beispiel: Für Knoten auf Quaderelementen sind nur die drei Translations-Freiheitsgrade verfügbar. Daher wird die Rotationsverschiebung nicht berechnet. Knoten auf Balkenelemente halten allen drei Rotationen Stand. Knoten auf Plattenelemente halten den beiden Rotationen in der Ebene Stand. Folgende Befehle stehen zur Verfügung:
- Größe: Legt fest, dass die Anzeige auf der Größe der Rotationsverschiebung basieren soll. Dies ist immer ein positiver Wert. Die Größe ist die Drehung, um den der Knoten insgesamt verschoben wurde. mag = sqrt[(rX)^2 + (rY)^2 + (rZ)^2]
- X: Legt fest, dass die Anzeige auf dem Punktprodukt des Rotationsvektors mit einem Einheitenvektor in X-Richtung basieren soll. Zeigt die Komponente der Gesamtrotation um die X-Achse an.
- Y: Legt fest, dass die Anzeige auf dem Punktprodukt des Rotationsvektors mit einem Einheitenvektor in Y-Richtung basieren soll. Zeigt die Komponente der Gesamtrotation um die Y-Achse an.
- Z: Legt fest, dass die Anzeige auf dem Punktprodukt des Rotationsvektors mit einem Einheitenvektor in Z-Richtung basieren soll. Zeigt die Komponente der Gesamtrotation um die Z-Achse an.
Die Rotationsergebnisse müssen in einer Analyse großer Verformungen (MES oder nichtlineare Analyse) mit mehreren Rotationen mit Vorsicht interpretiert werden. Die Rotationsergebnisse enthalten den gesamten Verlauf der Bewegung und sind daher abhängig vom Pfad. Als Beispiel dient die folgende Abbildung. (Die Verschiebungsergebnisse sind nicht vom Pfad abhängig.)
Ein L-förmiger Balken beginnt in der XZ-Ebene.
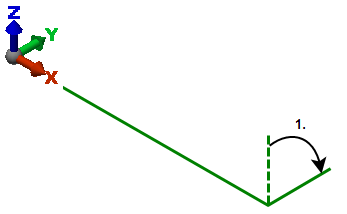
Der Balken wird in einem ersten Schritt um -90 Grad um die X-Achse gedreht.
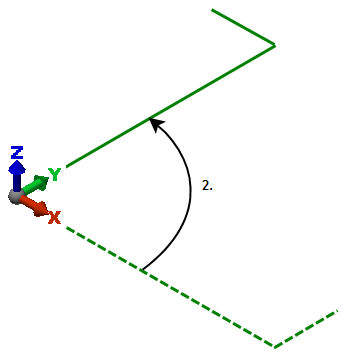
Im zweiten Schritt wird der Balken um 90 Grad um die Z-Achse gedreht.
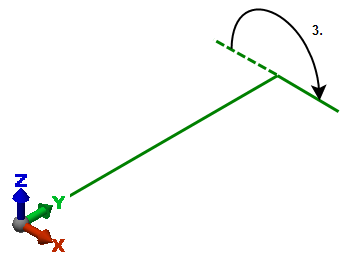
Im dritten Schritt wird der Balken um 180 Grad um die Y-Achse gedreht.
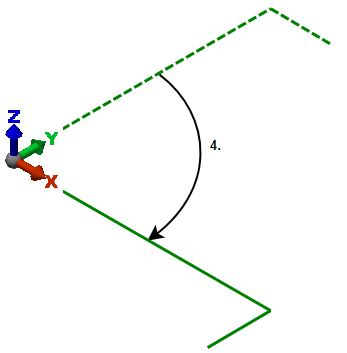
Im vierten Schritt wird der Balken um -90 Grad um die Z-Achse gedreht.
Wenn Sie die Endposition mit der Anfangsposition vergleichen, scheint es, als wären die endgültigen Rotationsergebnisse ein Nettowert von +90 Grad um die X-Achse und 0 Grad um die Y- und Z-Achse. In Analysen für große Verformungen sind die Ergebnisse -90 Grad um die X-Achse, 180 Grad um die Y-Achse und 0 Grad um die Z-Achse.
Da die Verschiebungsergebnisse vom Pfad unabhängig sind, lauten die endgültigen Verschiebungsergebnisse 0 in X sowie -L in Y und Z, wobei L für die Länge des kurzen Schenkels steht.
Im obigen Beispiel ist der Unterschied zur Option Große Festkörperdrehung (Einstellung im Dialogfeld Elementdefinition des Balkenelements) die Visualisierung der Balkenausrichtung. Die Ausrichtung der Achsen 2 und 3 ist nur bei Verwendung der großen Festkörperrotation korrekt.
Normalisierte Verschiebung und Drehung
- Eigenfrequenz (Modal)
Belastung
Es stehen verschiedene analytische Verfahren zur Verfügung, mit denen Sie die Eignung des Modells ermitteln können. In der Ergebnisanzeige haben Sie Zugriff auf viele dieser Verfahren, indem sowohl die Rohspannungen in lokalen Koordinaten als auch viele aus diesen Rohspannungen abgeleiteten Mengen bereitgestellt werden. Abgeleitete Mengen beinhalten von Mises- und Tresca-Kriterien, minimale und maximale Hauptspannung sowie elementspezifische Ausgaben. Da die Genauigkeit der analytischen Ergebnisse von der Konstruktion des Netzes und der Anwendung von FEM-Parametern abhängt, bietet die Ergebnisanzeige eine Genauigkeitsschätzung an gemeinsamen Knoten. Dieser Genauigkeitswert unterstützt Sie dabei, die Eignung des Modells zu bestimmen.
Analysen
Die Software verwendet die Spannung-zu-Knoten-Methode für die Berechnung von Spannungsschätzungen. Mithilfe eines Extrapolationsschemas bieten Berechnungen auf Grundlage der Knotenspannungen meist eine höhere Genauigkeit als Berechnungen, die anhand der Spannungen innerhalb der Elemente abgeleitet werden. Durch die Anzeige von Spannungen an Knoten wird eine realistischere und praktischere Darstellung eines Modells unter Last erzeugt, da die Spannungswerte an Knoten aussagekräftiger sind als die für das gesamte Element berechneten Spannungswerte.
Die für Elemente berechneten Spannungen haben Spannungsinformationen an Gaußschen Punkten zur Folge. Gaußsche Punkte sind die numerischen Integrationspunkte, an denen die finite Elementlösung und die theoretische Lösung die größte Ähnlichkeit aufweisen. Bei dem älteren Verfahren wurde der Durchschnitt dieser Spannungen an der Mitte oder den Flächen von 2D-Elementen und dem Zentroid von 3D-Elementen gebildet. Dieser konnte relativ große Unterschiede zwischen angrenzenden Elementen aufweisen. Da finite Elementlösungen eine Annäherung an eine kontinuierliche Funktion darstellen, sind die Ergebnisse für diese Positionen möglicherweise zu grob, um präzise abzubilden, wie sich ein Modell unter Spannung verhält.
Durch die Berechnung der Spannung an einzelnen Knoten wird dieses Problem behoben. Mithilfe der Methode der 'lokalen kleinsten Quadrate' werden die Spannungen anhand von Gaußschen Punkten zu den verknüpften Knoten extrapoliert. Eine genaue Bewertung der Spannungen an Knoten sind besonders wichtig, wenn sich die Knoten auf der Oberfläche oder Kante des analysierten Bauteils befinden, da diese Knoten im Allgemeinen mit kritischen Bereichen des Modells zusammenfallen. Genauigkeitsinformationen sind außerdem verfügbar, wenn Knoten von verschiedenen Elementen gemeinsam genutzt werden.
Beim Anzeigen der Oberfläche eines Modells werden die Intensität oder Spannung an jedem Punkt der einzelnen Elemente des Netzes, durch das die Oberfläche definiert ist, berechnet und dem Punkt ein entsprechender Anzeigewert zugeordnet. Anschließend werden die für die Anzeige der Oberfläche verwendete Skalierung überprüft und die entsprechenden Farben und Schattierungen für jeden Punkt basieren auf dem an diesem Punkt berechneten ausgewählt. Das Modell wird dann erneut gezeichnet, wobei die Oberfläche entsprechend dem verwendeten Anzeigeverfahren schattiert wird. Die Ergebnisanzeige enthält Visualisierungsoptionen, z. B. Glätten, mit denen Sie die Darstellung des Modells steuern können. Auf diese Weise können Sie das Modell in der für Sie geeigneten Weise visualisieren.
von Mises
Dieser Befehl legt fest, dass die Ergebnisanzeige die äquivalente von Mises-Spannung für eine Anzeige oder Datenausgabe enthält. Die von Mises-Spannung kann für Elementtypen mit einer Fläche (2D, Platten, usw.) und einem Volumen (Quader) angezeigt werden.
Verwendete Gleichung:
Dabei stehen Sx, Sy und Sz für die Axialspannungen in den globalen Richtungen und Sxy, Syz und Sxz für die Scherspannungen. In Bezug auf die Hauptspannung S1, S2 und S3 gilt:
Beachten Sie, dass der von Mises-Wert in den Gleichungen immer positiv ist.
Tresca*2
Die Tresca*2-Spannung kann für Elementtypen mit einer Fläche (2D, Platten usw.) und einem Volumen (Quader ) angezeigt werden. Diese Methode extrahiert die maximale Scherspannung aus dem folgenden Spannungstensor. Die Tresca-Gleichung lautet:
Dabei stehen S1, S2 und S3 für die Hauptspannungen. Der zurückgegebene Wert beträgt das Doppelte der maximalen Scherspannung. Damit tritt eine Streckung auf, wenn der zurückgegebene Tresca*2-Wert die Streckgrenze erreicht. Die Tresca-Spannung ist per Definition immer positiv. Eine Darstellung hiervon finden Sie unter Mohrs Kreis. Tresca*2 wird auch als Spannungsintensität bezeichnet.
Minimale Hauptspannung
Dieser Befehl legt fest, dass in der Ergebnisanzeige die minimale Hauptspannung (S3) für die Anzeige und Datenausgabe berechnet wird. Die Hauptspannung kann für Elementtypen mit einer Fläche (2D, Platten usw.) und einem Volumen (Quader ) angezeigt werden. Ein positives Vorzeichen (+) kennzeichnet Zug und ein negatives (-) Druck. Eine Darstellung hiervon finden Sie unter Mohrs Kreis.
Richtung der minimalen Hauptspannung
Durch diesen Befehl wird ein Vektorplot für die Richtung der minimalen Hauptspannung in jedem Element angezeigt. Die Tensoren an jedem Knoten des Elements werden gemittelt, und die Richtung der minimalen Hauptspannung dieses gemittelten Tensors wird am Zentroid des Elements ausgegeben. Wenn Sie ein Element markieren und Ergebnisse abfragen
Abfragen Aktuelle Ergebnisse auswählen, werden die Komponenten dieses Vektors angezeigt.
Mittlere Hauptspannung
Dieser Befehl legt fest, dass in der Ergebnisanzeige die mittlere Hauptspannung (S2) für die Anzeige und Datenausgabe berechnet wird. Diese Spannung wirkt lotrecht zur minimalen und maximalen Hauptspannung. Die Hauptspannung kann für Elementtypen mit einer Fläche (2D, Platten usw.) und einem Volumen (Quader ) angezeigt werden. Ein positives Vorzeichen (+) kennzeichnet Zug und ein negatives (-) Druck.
Richtung der mittleren Hauptspannung
Durch diesen Befehl wird ein Vektorplot für die Richtung der mittleren Hauptspannung in jedem Element angezeigt. Die Tensoren an jedem Knoten des Elements werden gemittelt, und die Richtung der mittleren Hauptspannung dieses gemittelten Tensors wird am Zentroid des Elements ausgegeben. Wenn Sie ein Element markieren und Ergebnisse abfragenAbfragenAktuelle Ergebnisse auswählen, werden die Komponenten dieses Vektors angezeigt.
Maximale Hauptspannung
Dieser Befehl legt fest, dass in der Ergebnisanzeige die maximale Hauptspannung (S1) für die Anzeige und Datenausgabe berechnet wird. Die Hauptspannung kann für Elementtypen mit einer Fläche (2D, Platten usw.) und einem Volumen (Quader ) angezeigt werden. Ein positives Vorzeichen (+) kennzeichnet Zug und ein negatives (-) Druck. Eine Darstellung hiervon finden Sie unter Mohrs Kreis.
Richtung der maximalen Hauptpannung
Durch diesen Befehl wird ein Vektorplot für die Richtung der maximalen Hauptspannung in jedem Element angezeigt. Die Tensoren an jedem Knoten des Elements werden gemittelt, und die Richtung der maximalen Haptspannung dieses gemittelten Tensors wird am Zentroid des Elements ausgegeben. Wenn Sie ein Element markieren und Ergebnisse abfragenAbfragenAktuelle Ergebnisse auswählen, werden die Komponenten dieses Vektors angezeigt.
Tensor
Dieser Befehl zeigt die Komponente der Spannung in der ausgewählten Richtung an. Technisch betrachtet wird das Doppelpunktprodukt mit dem Spannungstensor oder den lokalen Spannungskomponenten verwendet. Der Spannungstensor kann für Elementtypen mit einer Fläche (2D, Platten usw.) und einem Volumen (Quader ) angezeigt werden.
Wenn ErgebniskonturenEinstellungenLokale Elementergebnisse verwenden nicht aktiviert ist, können Sie zwischen den folgenden globalen Spannungen auswählen. Wenn diese Option aktiviert ist, werden bei den folgenden Auswahlen die in den einzelnen Beschreibungen angegebenen lokalen Spannungstensoren angezeigt.
Bei Elemente mit lokalen Achsen ist eine Glättung (Durchschnitt) der Spannungen möglicherweise nicht sinnvoll, insbesondere wenn die Ausrichtung der lokalen Achsen zwischen den angrenzenden Elementen variiert. Die geglätteten Spannungstensorwerte sind nur dann sinnvoll, wenn die lokalen Achsen von einem Element zum nächsten in gleichbleibender Richtung verlaufen.
- 1) XX: Spannungstensorkomponente für die normale Spannung in der globalen X-Richtung. Ein positives Vorzeichen (+) kennzeichnet Zug und ein negatives (-) Druck. Wenn ErgebniskonturenEinstellungenLokale Elementergebnisse verwenden aktiviert ist, wird der lokale Spannungstensor 1-1 angezeigt.
- 2) YY: Spannungstensorkomponente für die normale Spannung in der globalen Y-Richtung. Ein positives Vorzeichen (+) kennzeichnet Zug und ein negatives (-) Druck. Wenn ErgebniskonturenEinstellungenLokale Elementergebnisse verwenden aktiviert ist, wird der lokale Spannungstensor 2-2 angezeigt.
- 3) ZZ: Spannungstensorkomponente für die normale Spannung in der globalen Z-Richtung. Ein positives Vorzeichen (+) kennzeichnet Zug und ein negatives (-) Druck. Wenn ErgebniskonturenEinstellungenLokale Elementergebnisse verwenden aktiviert ist, wird der lokale Spannungstensor 3-3 angezeigt.
- 4) XY: Spannungstensorkomponente für die Scherspannung in der globalen XY-Richtung. (X steht für die Richtung lotrecht zur Fläche und Y für die Richtung der Scherspannung.) Wenn ErgebniskonturenEinstellungenLokale Elementergebnisse verwenden aktiviert ist, wird der lokale Spannungstensor 1-2 angezeigt.
- 5) YZ: Spannungstensorkomponente für die Scherspannung in der globalen YZ-Richtung. (Y steht für die Richtung lotrecht zur Fläche und Z für die Richtung der Scherspannung.) Wenn ErgebniskonturenEinstellungenLokale Elementergebnisse verwenden aktiviert ist, wird der lokale Spannungstensor 2-3 angezeigt.
- 6) ZX: Spannungstensorkomponente für die Scherspannung in der globalen ZX-Richtung. (Z steht für die Richtung lotrecht zur Fläche und X für die Richtung der Scherspannung.) Wenn ErgebniskonturenEinstellungenLokale Elementergebnisse verwenden aktiviert ist, wird der lokale Spannungstensor 3-1 angezeigt.
Balken und Stab
Durch diesen Befehl werden die Spannungen für lineare und nichtlineare Stabelemente, lineare und nichtlineare Balkenelemente und nichtlinearen Rohrelemente angezeigt. Folgende Ergebnisse sind verfügbar:
- Für nichtlinearen Analysen mit Balkenelementen, die Plastizität aufweisen, werden die durch diese Befehle angezeigten Ergebnisse nur teilweise um die Streckgrenze korrigiert. Jede Belastung (Axialspannung, Biegespannung in der lokalen Achse 2 und Biegespannung in der lokalen Achse 3) wird bei Bedarf auf die Streckgrenze gekürzt bzw. begrenzt. Für die ungünstigste Spannung werden dann die drei Ergebnisse addiert.
- Um ein präziseres Spannungsergebnis zu erhalten, aktivieren Sie die Option Binäre Spannungs- und Dehnungsausgabe in der Elementdefinition des Balkens, bevor Sie die Analyse ausführen. Überprüfen Sie die Ergebnisse anschließend in der Ergebnisanzeige durch Auswahl von Ergebnisse abfragenAbfragenDetaillierte Balkenspannung und Ergebnisse abfragenAbfragenDetaillierte Balkendehnung.
- Axialspannung (Richtung Lokal 1): Zeigt die Axialspannung an. Diese wird berechnet, indem die Axialkraft durch die Querschnittsfläche dividiert wird. Ein positiver Wert kennzeichnet Zugspannung und ein negativer Wert Druckspannung.
- Biegespannung in Richtung Lokal 2: Zeigt die Biegespannung in Balkenelementen aufgrund eines Biegemoments um die lokale Achse 2 an. Diese wird berechnet, indem das Biegemoment um Achse 2 durch das Abschnittsmodul um die lokale Achse 2 dividiert wird. Die lokale Achse 2 verläuft durch den K-Knoten und ist lotrecht zum Balken. (Da Stabelemente nicht biegbar sind, ist diese Menüoption für Stabelemente nicht gültig.)
- Biegespannung in Richtung Lokal 3: Zeigt die Biegespannung in Balkenelementen aufgrund eines Biegemoments um die lokale Achse 3 an. Diese wird berechnet, indem das Biegemoment um Achse 3 durch das Abschnittsmodul um die lokale Achse 3 dividiert wird. Die lokale Achse 3 ist das Kreuzprodukt der lokalen Achse 1 und der lokalen Achse 2. (Da Stabelemente nicht biegbar sind, ist diese Menüoption für Stabelemente nicht gültig.)
- Schlechteste: An einer Ecke erzeugt die Kombination aus Axialspannung, Biegespannung um Achse 2 und Biegespannung um Achse 3 den höchsten absoluten Wert. Dies ist die höchste Spannung in dem Balken. Für lineare Spannungen kennzeichnet ein positives Vorzeichen (+) einen axialen Zug auf den Balken und ein negatives Vorzeichen (-) einen axialen Druck. Mathematisch gilt:
Höchste = (Vorzeichen von P/A)(ABS(P/A)+ABS(M2/S2)+ABS(M3/S3))
Eine Spannungsanalyse (sowohl lineare als auch nichtlineare) geht von einem symmetrischen Querschnitt aus (aufgrund von nur einer Eingabe oder nur einem berechneten Wert für S2 und S3). Die höchste Spannung könnte daher mathematisch betrachtet an einer nicht vorhandenen Position in einem nicht symmetrische Balken auftreten, z. B. an der unteren linken oder oberen linken Ecke von Abbildung 1.
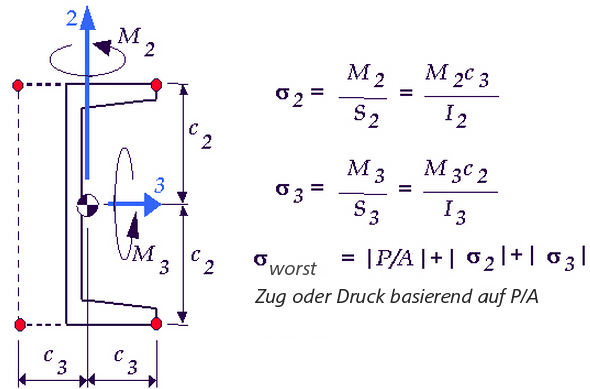
Abbildung 1: Spannungsergebnisse in einem nicht symmetrischen Balken
Aufgrund der Annahme, dass C2 und C3 gleich sind (auf nur einer Eingabe für S3 und S2 basieren), kann die höchste Spannung an einer nicht vorhandenen Position ausgegeben werden.
Verwenden Sie die Optionen Ergebnisoptionen Ansicht Elementausrichtung, um die lokalen Achsen 1, 2 oder 3 für die Balkenelemente anzuzeigen.
Zusammengesetztes Element
Fehlerkriterien
Durch diesen Befehl werden die Ergebnisse für die Fehlerkriterien des zusammengesetzten Elements in der Ebene angezeigt, die im Dialogfeld Elementdefinition festgelegt sind (Tsai-Wu, maximale Spannung oder maximale Dehnung).
Es wird empfohlen, die Glättung (Ergebniskonturen Einstellungen Ergebnisse glätten) zu deaktivieren, um den tatsächlichen Fehlerkriterienwert in jedem Element anzuzeigen (anstelle des geglätteten oder gemittelten Werts zwischen angrenzenden Elementen).
Sie können die Schicht, für die Ergebnisse angezeigt werden, unter ErgebniskonturenSpannungZusammengesetzte ElementeOptionen steuern. Darüber hinaus können Sie mit diesem Befehl die Ergebnisse für Schlechteste anzeigen.
Berücksichtigen Sie bei den Kriterien für die maximale Spannung und maximale Dehnung zunächst die folgenden Sicherheitsfaktoren, die auf der oberen und unteren Fläche der Schicht basieren:
Maximale Spannung - Sicherheitsfaktoren:
,
,
,
und 
Dabei stehen σ für die berechnete Normalspannung in Richtung 1 oder 2, X und Y für die zulässigen Spannungen in Richtung 1 und 2 (Druck oder Zug für die berechnete Spannung), τ12 für die berechnete Scherspannung und S für die zulässige Scherspannung.
Maximale Dehnung - Sicherheitsfaktoren:
,
,
,
und 
Dabei stehen ε für die berechnete Normaldehnung in Richtung 1 oder 2, T für die zulässige Dehnung in Richtung 1 und 2 (Zug oder Druck für die berechnete Dehnung), γ12 für die berechnete Scherdehnung und S für die zulässige Scherdehnung.
Die Ergebnisse werden anschließend wie folgt angezeigt:
| Fehlerindex für maximale Spannung und maximale Dehnung | |
|---|---|
| Lineare Spannung | Nichtlineare Spannung |
| Berechnen der Werte für 1/Sicherheitsfaktor | Berechnen der Werte für Sicherheitsfaktor |
| Plotten des höchsten Werts | Plotten des niedrigsten Werts |
| Werte >1 kennzeichnen einen Fehler. | Werte <1 kennzeichnen einen Fehler. |
Ziehen Sie für das Fehlerkriterium Tsai-Wu zunächst den Wert F heran:
Dabei gilt:
σ und τ sind die berechnete Normal- und Scherspannung, und alle anderen Werte sind Materialeingaben.
Die Ergebnisse werden anschließend wie folgt angezeigt:
| Fehlerindex für Tsai-Wu | |
|---|---|
| Lineare Spannung | Nichtlineare Spannung |
| Plotten des Werts F | Plotten des Werts 1/F |
| Werte >1 kennzeichnen einen Fehler. | Werte <1 kennzeichnen einen Fehler. |
Fehler aus der Ebene heraus
Wenn Sie dicke Verbundelemente mit dem Fehlerkriterium für die maximale Spannung verwenden, ist diese Option verfügbar, mit der Sie die Fehlerkriterienergebnisse durch die Dicke (Richtung aus der Ebene heraus) der Kernschicht anzeigen können. Die ausgegebenen Ergebnisse sind jeweils der höchste Wert für:
, 
und 
.
Dabei stehen σKern für die berechnete Normalspannung im Kern (in Richtung 3), Zc für die zulässige Kernzerkleinerungsspannung, τ für die berechnete Scherspannung und S für die zulässige transversale Scherspannung.
Ein Wert größer als 1 kennzeichnet einen Fehler.
Spannung
Die meisten der zuvor beschriebenen Formeln für die Spannungsergebnisse können verwendet werden, um die Dehnungsergebnisse in einem Modell anzuzeigen. Ersetzen Sie den Begriff Spannung in den Beschreibungen und Formeln einfach durch Dehnung. In diesen Situationen enthält die die Beschreibung weiter unter einen Link zu der entsprechenden Seite. Befehle für Dehnungsergebnisse, die deutliche Unterschiede zu den entsprechenden Befehlen für die äquivalente Spannung aufweisen, werden im Folgenden beschrieben.
- von Mises: Zeigt die äquivalente Dehnung mithilfe der von Mises-Gleichung an. Weitere Informationen finden Sie in der Beschreibung der von Mises-Spannung.
- Tresca*2: Zeigt die äquivalente Dehnung unter Verwendung des doppelten Tresca-Dehnungswerts an. Weitere Informationen finden Sie in der Beschreibung der Tresca-Spannung.
- Minimale Hauptdehnung: Zeigt die minimale Hauptdehnung an. Weitere Informationen finden Sie in der Beschreibung der minimalen Hauptdehnung.
- Maximale Hauptdehnung: Zeigt die maximale Hauptdehnung an. Weitere Informationen finden Sie in der Beschreibung der maximalen Hauptdehnung.
- Tensor: Zeigt eine Komponente der Dehnung in der ausgewählten Richtung an. Für eine statische Spannungsanalyse mit linearen Materialmodellen kann die Dehnungen in Elementkoordinaten sowie global oder zylindrischen Koordinaten angezeigt werden (ebenso wie die Spannungen). Anmerkung: Bei MES-Analysen sind Engineering-Dehnungsergebnisse verfügbar, keine Dehnungstensorergebnisse an. In der folgenden Matrix wird die Engineering-Dehnung (MES) dargestellt:wobei die Tensordehnung (Linear) angegeben wird durch:
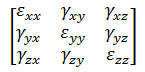
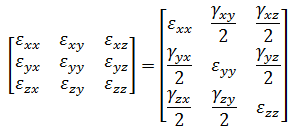
- Balken und Stab: Das Dehnungsmenü für Balken- und Stabelemente enthält die folgenden Optionen.
- Axialkraft: Zeigt die Axialdehnung aufgrund der Last entlang der Achse des Balkens/Stabs an. Die Zugsdehnung ist positiv.
- Biegung um Achse 2: Zeigt die maximale Faserdehnung aufgrund eines Moments um Achse 2 an. Dies gilt nur für Balken. Die Zugsdehnung ist positiv.
- Biegung um Achse 3: Zeigt die maximale Faserdehnung aufgrund eines Moments um Achse 3 an. Dies gilt nur für Balken. Die Zugsdehnung ist positiv.
- Schlechteste Kombination: Zeigt für Balkenelemente die ungünstigste Kombination aus Axial- und Biegedehnung um Achse 2 und Biegedehnung um Achse 3 an. Mathematisch gilt:
Höchste = (Vorzeichen von P/A)(ABS(P/A)+ABS(Dehnung um Achse 2)+ABS(Dehnung um Achse 3))
Für Stabelemente entspricht die höchste Dehnung der axialen Dehnung (P/A).
Dehnungsenergiedichte
Bei Auswahl dieses Befehls wird das Modell entsprechend der Dehnungsenergiedichte schattiert. Die Dehnungsenergie eines Elements ist als die Energie definiert, die das Element aufgrund der Last aufnimmt. Dies kann abhängig vom Volumen wie folgt berechnet werden: 
.
Normalisierte Spannung und Dehnung
- Eigenfrequenz (Modal)
Der einzige Zweck dieser Ergebnisse ist es, die relative Spannungs- und Dehnungsverteilung im Modell darzustellen. Das heißt, Sie können die Bereiche der maximalen oder minimalen Spannung und Dehnung ermitteln, jedoch die Ergebnisse allein mit der Modalanalyse nicht quantifizieren. Da die Ergebnisse auf keine bestimmte Erregung skaliert sind, sind die absoluten Spannungs- und Dehnungswerte nicht von Bedeutung.
Autodesk Moldflow-Ergebnisse
Gegebenenfalls können Autodesk Simulation Mechanical-Modelle in Autodesk Moldflow Adviser oder Insight zur Simulation des Spritzgussprozesses exportiert werden. Wenn eine Moldflow-Simulation abgeschlossen ist, sind zusätzliche Ergebnisse zur Visualisierung in der Ergebnisanzeige von Autodesk Simulation Mechanical verfügbar. Wählen Sie diese Ergebnisse in der Gruppe Moldflow-Ergebnis auf der Registerkarte Ergebniskonturen der Multifunktionsleiste aus.
Unter den linearen Analysetypen sind die Moldflow-Ergebnisse nur für Statische Spannung mit linearen Materialmodellen verfügbar. Moldflow-Ergebnisse sind auch für alle nichtlinearen Strukturanalysen verfügbar, mit Ausnahme derEigenfrequenz (Modal) mit nichtlinearen Materialien. Die folgenden Ergebnisse stehen zur Verfügung:
- Das Dropdown-Menü Restspannungstensor wird verwendet, um eine von sechs Restspannungstensorkomponenten auszuwählen (XX, YY, ZZ, XY, YZ und ZX). Diese Komponenten basieren auf den Hohlraum-Bauteilspannungen nach Abschluss des Spritzgussprozesses in der Moldflow-Simulation. Dies sind die Spannungen, bei denen die Formenabhängigkeit weiterhin gegeben ist, und diese Restspannungen führen dazu, dass sich ein Bauteil verformt, wenn dieses aus der Form freigegeben wird.
- Das Dropdown-Menü CTE-Tensor wird verwendet, um die Tensorkomponenten für Thermischer Ausdehnungskoeffizient in sechs Richtungen (XX, YY, ZZ, XY, YZ und ZX) auszuwählen. Dies sind die layerbasierten CTE-Ergebnisse aus der Moldflow-Analyse. Alle sechs CTE-Tensorkomponenten stehen nicht für alle Materialien zur Verfügung. Nur Materialien mit definierten anisotropen thermischen Eigenschaften verfügen über sechs CTE-Komponenten.
Elementverschiebungen
Die Ergebnisse unter Elementkräften und Momenten beziehen sich primär auf Linienelemente: Stäbe, Abstände, Balken, Begrenzungselemente usw.
- Ausdehnung: Dieser Befehl wendet eine Farbe auf das Abstands-, Begrenzungs-, Stab- oder Federelement basierend auf der Längenänderung an. Bei Abstands-, Stab- und Federelementen kennzeichnet ein positiver Wert einen Zug. Bei Begrenzungselementen deutet ein positiver Wert auf einen Druck hin.
- Drehen: Durch diesen Befehl wird auf die Begrenzungselemente eine Farbe basierend auf der Rotation des Elements angewendet. Die Richtung entspricht der Rechte-Hand-Regel vom Verbindungsknoten des Elements zum freien Ende.
Elementkräfte und Momente
Die Ergebnisse unter Elementkräften und Momenten beziehen sich primär auf Linienelemente: Stäbe, Abstände, Balken, Begrenzungselemente usw.
- Axiale Kraft: Zeigt die axiale Kraft (Richtung der lokalen Achse 1) für alle Linienelementtypen (Stab-, Balken-, Feder-, Abstands- und Begrenzungselemente) an. Bei Stab-, Feder- und Abstandselementen kennzeichnet ein positiver Wert einen Zug und ein negativer einen Druck. Bei Begrenzungselementen deutet ein positiver Wert auf einen Druck und ein negativer auf einen Zug hin. Informationen zu Balkenelementen finden Sie im Abschnitt zur Richtung von lokalen Kräften und Momenten für Balkenelemente weiter unten.
- Schubkraft in Achse 2: Zeigt die Schubkraft in der lokalen Richtung 2 für Balkenelemente an.
- Schubkraft in Achse 3: Zeigt die Schubkraft in der lokalen Richtung 3 für Balkenelemente an.
- Drehmoment: Zeigt die Torsion in einem Balkenelement (Moment um die lokale Achse 1) und Rotationsbegrenzungselementen an. Bei Begrenzungselementen folgt die Richtung der Torsion im Element an dem Verbindungsknoten zum Modell der Rechte-Hand-Regel vom Verbindungsknoten des Elements zum freien Ende. Informationen zu Balkenelementen finden Sie im Abschnitt zur Richtung von lokalen Kräften und Momenten für Balkenelemente weiter unten.
- Drehmoment um Achse 2: Zeigt das Drehmoment um die lokale Achse 2 für Balkenelemente an.
- Drehmoment um Achse 3: Zeigt das Drehmoment um die lokale Achse 3 für Balkenelemente an.
- Biegemoment der Platte: Bei Aktivierung wird der Biegemomenttensor
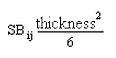
für alle Spannungsanalysen für Platten verwendet. Der Biegemomenttensor ist ein verteiltes Moment (Linienmoment, Moment pro Längeneinheit). Die Ergebnisse, die sich am einfachsten interpretieren lassen, werden durch die Option Ergebniskonturen Spannung Tensor ausgegeben. Die mathematische Berechnungen für von Mises-Spannung, Tresca-Spannung sowie minimale und maximale Hauptspannung werden durchgeführt, liefern jedoch ähnliche Ergebnisse wie die Biegespannungswerte multipliziert mit
.
Richtung der lokalen Kräfte und Momente für Balkenelemente:
| Komponente | Unterzug |
|---|---|
| Lokale Kraft 1 | Ein positiver Wert (+) kennzeichnet einen Zug, ein negativer Wert (-) einen Druck. |
| Lokale Kraft 2 |
|
| Lokale Kraft 3 |
|
| Lokales Moment 1 |
|
| Lokales Moment 2 |
|
| Lokales Moment 3 |
|
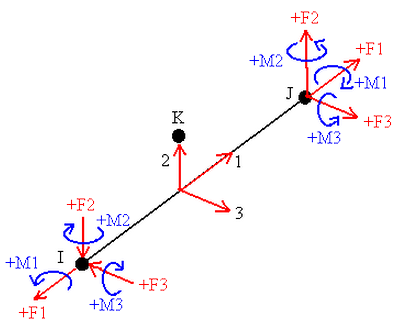
Abbildung 2: Richtung der lokalen Kräfte und Momente für Balkenelemente
Potenz-Spektraldichte
Wenn die Analyse der zufälligen Schwingungen ausgeführt wird und die Option für die Ausgabe der Dichte des Leistungsspektrums aktiviert ist, enthalten die ERGEBNISSE das Element Dichte des Leistungsspektrums. (Weitere Informationen über diese Option finden Sie auf der Seite Zufällige Schwingung.) Die Potenz-Spektraldichte kann wie folgt dargestellt werden:
- Zeigen Sie beliebige Ergebnistypen für das Modell an, z. B. Verschiebung oder Spannung.
- Wählen Sie den bzw. die Knoten aus, an denen eine Potenz-Spektraldichte sinnvoll ist, klicken Sie mit der rechten Maustaste, und wählen Sie Graphenwert(e) aus.
- Wählen Sie nach dem Erstellen des Diagramms Ergebnisse abfragen Diagramme Potenz-Spektraldichte aus, um eines der folgenden Ergebnisse anzuzeigen:
- X-Verschiebung: Zeigt die Dichte des Leistungsspektrums der X-Verschiebung an.
- Y-Verschiebung: Zeigt die Dichte des Leistungsspektrums der Y-Verschiebung an.
- Z-Verschiebung: Zeigt die Dichte des Leistungsspektrums der Z-Verschiebung an.
- X-Drehung: Zeigt die Dichte des Leistungsspektrums der X-Drehung an.
- Y-Drehung: Zeigt die Dichte des Leistungsspektrums der Y-Drehung an.
- Z-Drehung: Zeigt die Dichte des Leistungsspektrums der Z-Drehung an.
Beachten Sie, dass die Ergebnisse relativ zu den Trägern sind. Sie beziehen sich auf eine Potenz-Spektraldichte in Bezug auf die verweisen auf Strom Spektrum Dichte in Bezug auf die Eingangserregung.
Wenn Sie mehrere Knoten ausgegeben wurden, muss die Potenz-Spektraldichte für jeden Knoten nacheinander aktiviert werden. Klicken Sie mit der rechten Maustaste auf den relevanten Knoten im Browser, und wählen Sie Aktivieren aus, bevor Sie das Ergebnis für die Potenz-Spektraldichte anzeigen. (Allgemeine Anweisungen finden Sie auf der Seite Graphergebnisse von Analysen.)
Reaktionen
Durch diesen Befehl werden die internen Kräfte und Reaktionskräfte angezeigt. Folgende Ergebnistypen werden angezeigt:
- Interne Kraft: Dieses Menü zeigt für lineare Elemente die Reaktion durch die interne Kraft an jedem Knoten an. Dies sind keine Stützreaktionen. Verwenden Sie hierfür den Befehl Restkräfte. Sie können entweder die Größe der Reaktionskraft oder die einzelnen Komponenten entlang der globalen Achsen anzeigen.
- Angewendete Kräfte: Zeigt die auf jeden Knoten angewendete Kraft an. Sie können entweder die Größe der angewendeten Kraft oder die einzelnen Komponenten entlang der globalen Achsen anzeigen.
- Reaktionskraft (negativ): Zeigt die Restkaft an jedem Knoten an (Summe der angewendeten Kraft und Reaktionskraft). Dies wird von den meisten Ingenieuren als Stützreaktionen eingestuft, außer dass die Restkraft die Kraft angibt, die das Modell auf die Umgebung ausübt. Die Restkräfte und Stützreaktionen haben den gleichen Wert und entgegengesetzte Vorzeichen. Sie können entweder die Größe der Restkraft oder die einzelnen Komponenten entlang der globalen Achsen anzeigen.
Bei MES/nichtlinearen Elementen werden in diesem Menü die Reaktionskräfte an jedem Knoten angezeigt. Die Ergebnisse sind an Randbedingungen, Zwangsverschiebungen, Aufprallwänden und Flächenkontakten ungleich Null.
- Internes Drehmoment: Dieses Menü zeigt für lineare Elemente die Reaktion durch das interne Drehmoment an jedem Knoten an. Dies sind keine Stützreaktionen. Verwenden Sie hierfür den Befehl Restmoment. Sie können entweder die Größe des Reaktionsmoments oder die einzelnen Komponenten entlang der globalen Achsen anzeigen.
- Angewendetes Moment: Zeigt das auf jeden Knoten angewendete Moment an. Sie können entweder die Größe des angewendeten Moments oder die einzelnen Komponenten entlang der globalen Achsen anzeigen.
- Reaktionsmoment (negativ): Zeigt das Restmoment an jedem Knoten an (Summe der angewendeten Momente und Reaktionsmomente). Dies wird von den meisten Ingenieuren als Stützreaktionen eingestuft, außer dass das Restmoment das Moment angibt, das das Modell auf die Umgebung ausübt. Die Restmomente und Stützreaktionen haben den gleichen Wert und entgegengesetzte Vorzeichen. Sie können entweder die Größe der Restkraft oder die einzelnen Komponenten entlang der globalen Achsen anzeigen.
Bei MES/nichtlinearen Elementen werden in diesem Menü die Reaktionsmomente an jedem Knoten angezeigt. Die Ergebnisse sind an Randbedingungen und Zwangsrotationen ungleich Null.
Für jeden Ergebnistyp stehen die folgenden Optionen zur Verfügung:
- Größe: Schattiert das Modell basierend auf der Größe des Ergebnisses.
- X: Schattiert das Modell basierend auf der X-Komponente des Ergebnisses.
- Y: Schattiert das Modell basierend auf der Y-Komponente des Ergebnisses.
- Z: Schattiert das Modell basierend auf der Z-Komponente des Ergebnisses.
- Vektorausgabe: Zeigt das Ergebnis als einen Pfeil an jedem Knoten an. Die Länge und Farbe des Pfeils gibt die Größe des Ergebnisses an, und die Richtung des Pfeils stellt die Vektorrichtung des Ergebnisses dar. Anmerkung: Die Reaktionskräfte/-momente und Restkräfte/-momente sind an allen mittels intelligenter Einbindung verbundenen Knoten ungleich Null. (Diese Ergebnisse bekaufen sich an der Begrenzung zwischen Bauteilen normalerweise auf 0.)
von Mises-Genauigkeit
Die Genauigkeit dient zur Hervorhebung von Änderungsstufen in den Ergebnissen zwischen zwei Elementen. In einem idealen Modell ändert sich die Spannung gleichmäßig zwischen zwei angrenzenden Elementen. Bei der Erstellung einer diskreten Auflösung des Modells mit Elementen treten immer gewisse Änderungen in den Ergebnisse von einem Element zum nächsten auf. Die Ergebnisse sind nicht fortlaufend.
Beispiel: In einem Spannungsmodell ermitteln Elemente mit gemeinsam verwendeten Knoten die Spannungen an dem jeweiligen Knoten unabhängig voneinander. Die unabhängigen Spannungsanalysen bieten daher eine Genauigkeitsschätzung für das Modell basierend auf der von Mises-Spannung. Der Genauigkeitswert an einem bestimmten Knoten wird wie folgt berechnet:
Die Genauigkeit variiert per Definition zwischen 0 (beste) und 0,5 (schlechteste). Knoten, die nicht von zwei oder mehr Elementen gemeinsam genutzten werden, weisen nur eine Spannungsschätzung und einen Genauigkeitsindex von 0 auf.
Beispiel 1:
Wenn die maximale von Mises-Spannung im Modell 200 beträgt, lautet die Genauigkeit an die folgenden Knoten wie folgt (bei bis zu drei mit dem Knoten verbundenen Elementen):
| Knotennummer | von Mises-Spannung | Genauigkeitswert | Kommentar | ||
|---|---|---|---|---|---|
| Wert 1 | Wert 2 | Wert 3 | |||
| 17 | 20 | -- | -- | 0,0 | Einzelner Elementknoten |
| 23 | 20 | 40 | 25 | 0,05 | 0,5(40-20)/200 |
| 36 | 150 | 120 | 200 | 0,20 | 0,5(200-120)/200 |
Beispiel 2:
Die folgende Abbildung zeigt vier Elemente um Knoten Nr. 5 und die folgenden Spannungen:
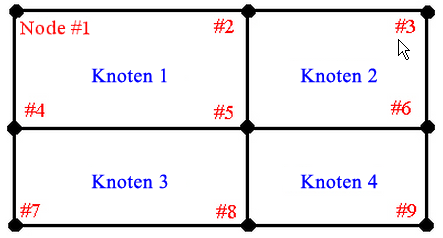
| Elementnummer | Knotennummer | von Mises-Spannung |
|---|---|---|
| 1 | 5 | 20.000 |
| 2 | 5 | 15.000 |
| 3 | 5 | 19.000 |
| 4 | 5 | 10.000 |
Wenn die maximale Spannung im Modell 25.000 beträgt (z. B. an Knoten 9), lautet die Genauigkeit an Knoten 5
Genauigkeit Knoten 5 = 0,5 (20.000 - 10.000)/25.000 = 0,2
Es kann nicht garantiert werden, dass die tatsächlichen Spannungen innerhalb des angegebenen Bereichs liegen. Der Bereich, in dem diese liegen, hängt von der Vernetzung des Modells und der Modellierung des tatsächlichen Bauteils sowie von weiteren Faktoren ab. Abweichungen unterhalb der angegebenen Genauigkeit können als unbedeutend betrachtet werden. Wenn beispielsweise als Genauigkeit 0,1 definiert ist und die maximale Spannung 200 beträgt, sind Abweichungen von weniger als 20 Spannungseinheiten irrelevant.
Angewendete Lasten
Durch Auswahl dieser Option wird das Modell mit den Eingangslasten angezeigt. Verfügbare Lasten für eine Strukturanalyse sind die Temperatur und die Spannung.
- Für eine lineare Spannung:
- Der Befehl Ergebniskonturen Sonstige Ergebnisse Angewendete Lasten Temperatur ist immer verfügbar.
- Die Kontur wird für alle in den Analysenparametern angegebenen Arten von Temperaturlasten aus der Modelldatei, der stationären Wärmeübertragung oder der transienten Wärmeübertragung angezeigt.
- Die Auswirkungen der Temperatur auf die Analyse hängt außerdem von der spannungsfreuen Referenztemperatur und dem thermischen Multiplikator ab. Diese Abhängigkeiten werden in der Temperaturkontur nicht angezeigt.
- Der Befehl Ergebniskonturen
- Für mechanischen Ereignissimulator/nichtlineare Spannung:
- Der Befehl Ergebniskonturen Sonstige Ergebnisse Angewendete Lasten Temperatur ist nur verfügbar, wenn dem Modell in den Analysenparametern eine Quelle für die Knotentemperatur zugewiesen wurde.
- Die Kontur wird nur für die Temperaturlast aus der Modelldatei angezeigt. Temperaturkonturen aus stationären und transienten Wärmeübertragungsanalysen sind nicht für die Ausgabe verfügbar.
- Die Auswirkungen der Temperatur hängen außerdem von der spannungsfreien Referenztemperatur und dem Lastkurvenmultiplikator ab. Der Effekt des Lastkurvenmultiplikators wird durch die Temperaturkontur dargestellt.
- Der Befehl Ergebniskonturen
Elementeigenschaften
Diese Befehle schattieren das Modell auf Grundlage der Form der Elemente. Die meisten Befehle gelten nur für Flächen- und Volumenelemente, darunter 2D-, Platten-, Quaderelemente usw.
Durch die folgenden Optionen wird das Modell basierend auf dem ausgewählten Element schattiert.
- Volumen: Wenn die Option Analyse Analyse Gewicht und Schwerkraft auf das Modell angewendet wird und Sie den Befehl Ergebniskonturen Sonstige Ergebnisse Elementeigenschaften Volumen auswählen, wird das Volumen jedes Elements angezeigt. Der Gewichts- und Schwerkraftrechner wird automatisch ausgeführt, wen im Dialogfeld Abfragen: Ergebnisse eine gewichtete Ergebnisübersicht berechnet wird.
- Torsionswinkel: Die Torsion eines vierseitigen Elements (4 Knoten) oder einer Fläche eines Volumenkörperelements mit vier Knoten wird angezeigt. Der Torsionswinkel kann mithilfe von vier Methoden berechnet werden.
- Methode der minimalen Faltung oder Methode der maximalen Faltung: Bei Auswahl eines dieser Befehle werden die beiden vierseitigen Faltwinkel berechnet und der minimale bzw. maximale Faltwinkel verwendet. Der vierseitige Faltwinkel wird ermittelt, indem das vierseitige Element in zwei Dreiecke unterteilt wird (durch Hinzufügen einer der zwei möglichen Diagonalen). Der Faltwinkel ist der Winkel zwischen den Ebenennormalen dieser beiden Dreiecke.
- Methode der Mittelebene: In diesem Fall ist der Sinus des Mittelebenenwinkels gleich der Höhe eines beliebigen Endknotens oberhalb der Mittelebene dividiert durch die Hälfte der Länge der kürzesten Seite. Die Mittelebene ist die Ebene, die alle vier Mittelpunkte der Kantenlinien enthält. Jeder Knoten hat den gleichen Abstand von dieser Ebene. Der Torsionswinkel wird berechnet, indem der Mittelebenenwinkel mit 2*Quadratwurzel aus (2) multipliziert wird, sodass er mit dem Faltwinkel für mit kleinem Winkel gebogene Quadrate vergleichbar ist. Der Faktor 2 ergibt sich durch die Verwendung des Winkels aus der Mittelebene anstelle des kompletten Faltwinkels. Der Faktor der Quadratwurzel von (2) ergibt sich aus der Division durch eine halbe Seite anstelle einer halben Diagonalen.
- Knotenwinkel: Bei Aktivierung werden Elemente basierend auf dem größten Knotenwinkel (Innenwinkel) einer beliebigen Fläche des Elements angezeigt.
- Seitenverhältnis: Bei Aktivierung werden die Elemente basierend auf ihrem Seitenverhältnis angezeigt.
Bei dreieckigen Elemente entspricht das Seitenverhältnis der längsten Seite dividiert durch die Höhe des Dreiecks über dieser längsten Seite. Dieses Verhältnis wird mit der Quadratwurzel von (3/4) multipliziert, sodass ein gleichseitiges Dreieck ein Seitenverhältnis von 1,0 aufweist.
Bei vierseitigen Elementen (Platten und 2D) wird das Seitenverhältnis wie folgt berechnet: Die Länge der längsten Seite wird durch den größten Abstand von der längsten Seite zu einem anderen Knoten des vierseitigen Elements dividiert. Ein Quadrat hat ein Seitenverhältnis von 1,0. Ein Rechteck mit Seiten von 1 und 2 hat ein Seitenverhältnis von 2,0.
Bei Quaderelementen (8 Knoten) werden die Mittelpunkte der drei Paar gegenüber liegender Flächen so verbunden, dass sich drei Linien ergeben. Diese Linien kreuzen den Mittelpunkt des Quaders, und jedes Linienpaar definiert eine Ebene. Für jede aus zwei Linien gebildete Ebene wird das Verhältnis zwischen dem Abstand von der Ebene zu den Endpunkten der dritten Linie dividiert durch die Hälfte der Länge der längsten Linie in der Ebene berechnet. Das Seitenverhältnis für den Quader ist das größte dieser drei Verhältnisse. Bei rechteckigen Volumenkörper ist das Seitenverhältnis das größte Seitenverhältnis einer der Flächen.
Bei Keilelementen (Quader mit 6 Knoten) wird ein mittleres Dreieck anhand der Mittelpunkte der Kantenlinien gebildet, die die dreieckigen Flächen des Keils verbinden. Angenommen b ist die längste Seite des mittleren Dreiecks, h die Höhe des mittleren Dreiecks und hw die Länge der Linie zwischen den Mittelpunkten der Enddreiecke. Das Seitenverhältnis ist der maximale Wert aus sqrt(3)*h/(2*b), hw/b und b/hw. Ein Keil, der durch Extrusion eines gleichseitigen Dreiecks um einen der Seite entsprechenden Abstand erzeugt wurde, hat ein Seitenverhältnis von 1,0.
Bei Pyramidenelementen (Quader mit 5 Knoten) ist h die Höhe des Punkts über der Mittelebene des Vierecks. Angenommen b ist die längste Mittelkantenlinie des Vierecks, dann ist das Seitenverhältnis der Maximalwert des Seitenverhältnisses des Vierecks, h/b und b/h. Eine Pyramide mit einer quadratischen Basis und einer Höhe gleich der Basisseite hat ein Seitenverhältnis von 1,0.
Bei Tetraederelementen (Quader mit 4 Koten) wird die Höhe hi über dem Basisdreieck mit der Fläche ai für jede der vier möglichen Basiswerte berechnet. Das Seitenverhältnis ist der Maximalwert von Cf * hi/sqrt(ai), sqrt(ai)/(Cf * hi) für alle vier Basisdreiecke. Cf ist (3/4)^3/4, sodass das Seitenverhältnis eines Tetraeders mit gleichen Seiten 1,0 ist.
- Verhältnis Lang/Kurz: Bei Aktivierung werden Elemente basierend auf dem Verhältnis Lang/Kurz angezeigt. Das Verhältnis Lang/Kurz ist das Verhältnis der längsten Kantenlänge dividiert durch die kürzeste Kantenlänge.
- Verhältnis Fläche zu Volumen: Bei Aktivierung werden Volumenkörperelemente basierend auf dem Verhältnis der Fläche dividiert durch das Volumen angezeigt. Das Verhältnis Fläche/Volumen ist definiert durch die Quadratwurzel von (Fläche/6) dividiert durch die Kubikwurzel des Volumens. Ein Würfel hat ein Verhältnis Fläche/Volumen von 1,0. Flache Elemente (Platten) haben ein Verhältnis Fläche/Volumen von 1,0.
- Dicke der Platte: Dieser Befehl ist nur für Platten- oder Gehäuseelemente gültig. Die Kontur variiert abhängig von der Dicke dieser Elemente.
- Verhältnis der Tetraederausblendung: Dieser Befehl ist für Quadermodelle gültig, die Tetraederelemente mit 4 Knoten enthalten. Bei Auswahl dieses Befehls werden Tetraederelemente basierend auf dem Verhältnis der längsten Kantenlänge des Elements zur kürzesten Höhe (L/h) angezeigt. Die anderen Elementtypen werden nicht schattiert. Tipp: Da das gesamte Netz angezeigt werden muss, um die innere Elemente zu sehen, und da die Anzahl der Tetraederelemente in der Regel klein ist im Vergleich zu den anderen Elementtypen, ist das Ergebnis durch die Vielzahl der anderen, unschattierten Elemente möglicherweise nur schlecht zu erkennen. Mithilfe des Filtermoduls können Sie nur die schattierten Elemente auswählen und die nicht ausgewählten Elemente ausblenden.
- Länge des Elements: Bei Aktivierung werden Linienelemente (Balken, Stab usw.) basierend auf der Länge jedes Elements angezeigt. Die anderen Elementtypen werden nicht schattiert.