Итерационные решатели используются при решении уравнений, когда методы перестановки для линейных решателей неэффективны, а матрица жесткости K достаточно хорошо обусловлена.
Общие положения
Использовать итерационные решатели рекомендуется для хорошо обусловленных крупномасштабных задач (15 000-1 000 000 уравнений), линейных статических задач и задач на собственные значения (модальный расчет или расчет продольного изгиба).
Традиционные прямые методы, т.е. фронтальный метод, метод ненулевых элементов разреженной матрицы и разреженный метод, требуют много времени и большого объема дискового пространства для хранения разложенной на множители матрицы.
В то же время, итерационные решатели существенно сокращают время расчета и требуют меньшего объема памяти на жестком диске. Однако они имеют ряд недостатков:
- Медленное схождение при плохо обусловленных задачах.
- Поэтапный расчет каждого варианта нагружения с самого начала. Необходимость определения как можно меньшего количества вариантов нагружения.
Итерационные решатели эффективны для расчета конструкций, содержащих тела КЭ. Они также полезны при линейном статическом расчете (например, для поиска оптимальных проектных параметров), когда для нескольких вариантов нагружения можно получить приблизительные решения.
Поэлементное управление корректностью данных при регуляризации Vinget устанавливает дополнительное приложение итерационного решателя, что позволяет выявить сложности при поиске ошибок в модели КЭ.
Метод градиентов с предобусловливанием (PCG) включает в себя несколько типов подготовки предварительных условий.
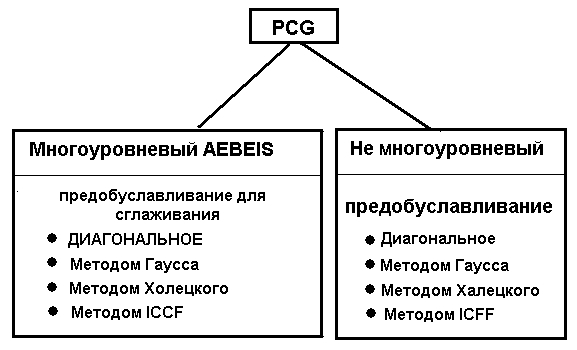
- AEBEIS: агрегационный поэлементный итерационный решатель 1,2.
- EBE: поэлементный метод.
- ICCF: техника неполной факторизации Холецкого.
Поэлементный (PCGEBE) и многоуровневый итерационный решатель (AEBEIS)
Поэлементный решатель (PCGEBE) используется для всех типов конечных элементов и не ограничен размером задачи. Однако он чувствителен к плохой обусловленности матрицы жесткости K, из-за чего возможна медленная сходимость.
Многоуровневый итерационный решатель (AEBEIS) — это многоуровневый агрегационный поэлементный интерактивный решатель, который сочетает в себе преимущества быстрых итерационных методов с недорогой технологией EBE. Этот решатель позволяет ускорить основные операции с помощью недорогого метода, учитывая требования к ресурсам памяти. Подобные методы агрегации позволяют выполнять расчеты для твердых тел и оболочек (как и многосеточные методы), а также для стержней и смешанных конструкций из стержней, оболочек и твердых тел.
Решатель AEBEIS по сравнению с немногоуровневыми методами обычно обеспечивает более быструю сходимость. Повышая стабильность сходимости плохо обусловленных задач, он является менее надежным. В редких случаях подготовка предварительных условий блокируется, в то время как сходимость по-прежнему является медленной. Этот решатель был реализован путем комбинирования агрегационного решателя на основе методики EBE.
Решатель AEBEIS дает возможность применять двумерные и трехмерные стержневые элементы, оболочки (3, 4, 6, или 8 узловых элементов) и твердотельные элементы. Он также включает дополнительные элементы конструкции, такие как упругие опоры, смещения, выпуски и жесткие связи. Для немногоуровневого метода не существует ограничений по типам элементов или конструкций.
Следующие типы симметричной обусловленности доступны как для AEBEIS, так и для немногоуровневых методов.
- Диагональ — симметричная обусловленность Якоби (применяется только для хорошо обусловленных задач).
- EBE Гаусса — симметричная обусловленность Холецкого-Гаусса-Сейделя. 12.
- EBE Холецкого — симметричная обусловленность Холецкого EBE 34.
- ICCF — метод неполной факторизации Холецкого 56.
Метод ICCF быстрее, чем другие методы (диагональ, EBE Гаусса, EBE Холецкого) и использует примерно то же количество итераций для получения сходимости, что и методы EBE Гаусса и EBE Холецкого. Этот метод не использует операции ввода/вывода на жестком диске, однако предъявляет высокие требования к производительности оперативной памяти. ICCF является предпочтительным вариантом, если на компьютере имеется достаточно памяти для выполнения задачи. В свою очередь, методы EBE Гаусса и EBE Холецкого предъявляют минимальные требования к ОЗУ и производительности жесткого диска, однако скорость их выполнения значительно ниже метода ICCF.