Чтобы задать параметры модального расчета для новых вариантов динамических нагружений в конструкции, выполните одно из следующих действий:
- Выберите вар модального расчета в диалоговом окне Новое нагружение и нажмите кнопку ОК.
- Выберите модальный расчет в диалоговом окне Тип расчета и нажмите кнопку Настроить параметры;
Рекомендуется применение итерационного решателя для решения задач большого порядка, так как он содержит три способа решения проблем собственных значений. Для этого, в Рабочих настройках, выберите опцию Итерационное решение в дилоговом окне Расчет конструкции.
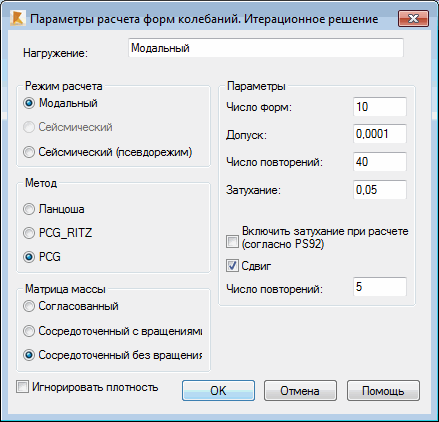
Режим расчета:
В текущей версии, для итерационного решателя доступны следующие режимы расчета: модальный и сейсмический псевдорежим. Модальный режим доступен только для предварительно обусловленных сопряженных градиентов (PCG) [1-4]. Сейсмический псевдорежим доступен для модифицированного метода Ланцоша и метода Ритца (PCG_Ritz).
Метод
Метод Ланцоша
Ланцош – это модифицированный метод Ланцоша, позволяющий избежать факторизации матрицы большого порядка. При помощи метода предварительно обусловленных сопряженных градиентов (PCG) формируется совокупность векторов Ланцоша вместо выполнения обратного разложения факторизованной матрицы жесткости. Доступны все предварительно обусловленные типы, заданные для статического расчета ( Инструменты > Рабочие настройки > Итерационный > Параметры).
Модифицированный метод Ланцоша предпочтительней использовать для сейсмического расчета и спектрального анализа больших конструкций, когда требуется много режимов.
- Требуемые параметры
Тип матрицы масс (сосредоточенная с вращением или согласованная) и количество форм.
Точность расчета зависит от принятого допуска при расчете векторов Ланцоши и Количества форм. Допуск задается в окне Инструменты > Рабочие настройки > Итерационный > Параметры и является таким же, как и для статических вариантов нагружения. Допуск, фигурирующий в диалоговом окне "Параметры модального расчета. Итерационное решение" — это допуск для решения обобщенной задачи собственных значений, включая заданные вектора Ланцоша и он не может быть меньше 1,0e – 04.
Чем большее количество форм будет учтено в расчете, чем ближе будут нижние вектора Ритца к соответствующим собственным значениям. Тем точнее будет сумма модальных масс.
Предобусловленные градиенты_Ритц (PCG_Ritz)
PCG_Ritz - это метод Ритца, в котором для создания группы основных векторов используется приближение предварительно обусловленных градиентов (градиентный метод Ритца [5]). Метод PCG_Ritz является предпочтительным для проведения аппроксимации быстрых определений собственных пар во время проведения сейсмического расчета и спектрального анализа. Необходимо выбрать многоуровневой метод. Также рекомендуется назначить один уровень агрегирования. Этот метод будет эффективным для средних задач (до 60,000 уравнений). Все предварительно обусловленные типы, заданные для статического расчета, доступны в диалоговом окне ("Инструменты" > "Рабочие настройки" > "Итерационный" > "Параметры").
- Требуемые параметры
Тип матрицы масс (сосредоточенная с вращением или согласованная) и количество форм. Точность расчетов зависит от Количества форм.
Предварительно обусловленные сопряженные градиенты
PCG – это метод предварительно обусловленных сопряженных градиентов [1-5], использование которого является предпочтительным, если задано малое количество собственных форм. Например, метод PCG рекомендован к использованию во время применения ветровых нагрузок или проверки небольшого количества низких форм, полученных при помощи метода PCG_Ritz. Все предварительно обусловленные типы, заданные для статического расчета, доступны в диалоговом окне ("Инструменты" > "Рабочие настройки" > "Итерационный" > "Параметры"). Могут применяться все типы матрицы масс (согласованная, сосредоточенная с вращением или сосредоточенная без вращения).
- Требуемые параметры:
Количество форм; Допуск - критерии точности, касающиеся остановок итераций; Количество итераций - максимальное допустимое количество итераций для каждого режима (процесс итерации для каждого режима останавливается, если текущий параметр допуска меньше, чем Допуск или если текущее количество итераций превышает Количество итераций); Сдвиг - использует технику сдвига для ускорения сходимости; Количество повторений - определяет количество повторений (для каждого режима алгоритм выполняет количество итераций, определенных Количеством интераций, исправляет значение переключения и повторяет итерации, заданные Количеством итераций столько раз, сколько задано Количеством повторений).
- Рекомендуемые параметры:
Многоуровневый или немногоуровневый метод с ICCF приближением ("Инструменты" > "Рабочие настройки" > "Итерационный" > "Параметры"); к.Форм £ 5; Допуск = 0,01; Количество итераций = 100 для немногоуровневого метода; опция Сдвиг - отключена
- Тип матрицы масс.
- Параметры (количество форм, допуск, количество итераций, затухание)
- Сдвиг (с количеством итераций).
Предотваращение неправильной настройки параметров итерационного решателя.
Система контроля, позволяющая предотвратить некорректное задание параметров модального расчета для итерационных решателей. Она включется после нажатия кнопки ОК для запуска модального расчета. На экране высвечивается диалоговое окно параметров расчета. Нажмите кнопку Да для того, чтобы принять значения параметров, заданных в диалоговом окне. Нажмите кнопку Нет для того, чтобы вернуться к диалоговому окну Параметры модального расчета и внести исправления в значениях параметров.
Если при расчете используется итерационное решение в Сейсмическом псевдорежиме, тогда выполните следующие действия:
- Количество степеней агрегирования должно равняться 1 (параметр задается в диалоговом окне Рабочие настройки > Расчет конструкции / Параметры > Итерационный)
- Искомое количество форм должно вводиться как минимум в три раза больше, чем требуется.
- Сходимость результатов должна быть проверена для количества форм, показанных в пункте 2 и количество форм - в два раза больше. В случае отсутствия сходимости (безусловно разные собственные значения для количества форм в два раза больше, чем для начального количества), количество форм должно быть увеличено. После того, как получено сходящееся решение, нужно применить фильтрацию форм для ограничения их количества.
Для такого типа расчета, параметр Допуск в результатах динамического расчета не имеет практического значения и может не учитываться. Если не следовать приведенным рекомендациям, ошибка может достигать нескольких десятков процентов.
Список литературы
- Дж. Гамболати, Дж. Пини, Ф. Сарторетто "Усовершенствованный итерационный метод оптимизации для самых левых собственных пар больших симметрических матриц", опубл. в "Journal of Computational Physics", 74: 41 - 60, 1988.
- Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Physics",81: 53 - 69, 1989.
- Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Мет. Прилож. Мех. Инж., 62: 195 - 207, 1987.
- М.Пападракис, Решение задач большого порядка в механике, John Wiley & Sons Ltd., 1993.
- Фиалко С., "Высокоэффективный Ритц-градиент метод поэлементной агрегации для расчета динамической реакции конструкции", CAMES, 7: 537-550, 2000.
См. также:
Допущения при модальном расчете
Параметры модального расчета с учетом статических сил
Описание модального расчета с распознаванием статических сил
Описание метода блочной итерации подпространства