Существует несколько типов итерационных решателей.
Итерационный метод ICCF
Этот метод рекомендуется использовать для крупномасштабных задач с небольшим количеством правых сторон.
- Использование памяти: высокое.
- Использование диска: не используется.
- Оценка скорости: высокая (для хорошо обусловленных задач).
- Количество уравнений: 15 000-1 000 000 и более.
- Поддерживаемые расчеты: линейный статический расчет, модальный расчет и расчет продольного изгиба.
- Возможные ограничения расчета: не определено
- Другие ограничения:
- При корректировке конструкции ограничения не установлены.
- Низкая сходимость при некорректной обусловленности задач.
Итерационная диагональ
Этот метод рекомендуется использовать для крупномасштабных задач с небольшим количеством правых сторон.
- Использование памяти: минимальное
- Использование диска: минимальное
- Оценка скорости: низкая
- Количество уравнений: 15 000-1 000 000 и более.
- Поддерживаемые расчеты: линейный статический расчет, модальный расчет и расчет продольного изгиба.
- Возможные ограничения расчета: не определено
- Другие ограничения:
- При корректировке конструкции ограничения не установлены.
- Низкая сходимость при некорректной обусловленности задач.
Итерационный метод Гаусса-Холецкого
Данный метод рекомендуется использовать для крупномасштабных задач с небольшим количеством правых сторон, если для работы с методом ICCF имеется недостаточно памяти.
Проверка каждого элемента матрицы осуществляется с помощью процедуры регуляризации Vinget. 12.
- Использование памяти: минимальное
- Использование диска: минимальное
- Оценка скорости: низкая
- Количество уравнений: 15 000-1 000 000 и более.
- Поддерживаемые расчеты: линейный статический расчет, модальный расчет и расчет продольного изгиба.
- Возможные ограничения расчета: не определено
- Другие ограничения:
- При корректировке конструкции ограничения не установлены.
- Низкая сходимость при некорректной обусловленности задач.
Итерационный многоуровневый метод ICCF
Этот метод рекомендуется использовать для крупномасштабных задач с небольшим количеством правых сторон. Здесь сходимость достигается быстрее, чем при использовании итерационного метода ICCF.
- Использование памяти: высокое
- Использование диска: минимальное
- Оценка скорости: высокая (для хорошо обусловленных задач)
- Количество уравнений: 15 000-1 000 000 и более.
- Поддерживаемые расчеты: линейный статический расчет, модальный расчет и расчет продольного изгиба.
- Возможные ограничения расчета: доступные типы конструкций: трехмерные (стержень, оболочка, твердое тело и все специальные конечные элементы), плоская рама.
- Другие ограничения:
- При корректировке конструкции ограничения не установлены.
- Менее устойчивая сходимость в редких случаях.
Итерационная многоуровневая диагональ
Этот метод работает значительно медленнее, чем итеративный многоуровневый метод ICCF. Однако он требует значительно меньше оперативной памяти.
Метод сглаживания 2 обычно требует меньшее количество итераций по сравнению с итерационным многоуровневым методом ICCF.
Проверка каждого элемента матрицы осуществляется с помощью процедуры регуляризации Vinget 1,2.
- Использование памяти: минимальное
- Использование диска: минимальное
- Оценка скорости: низкая
- Количество уравнений: 15 000-1 000 000 и более.
- Поддерживаемые расчеты: линейный статический расчет, модальный расчет и расчет продольного изгиба.
- Возможные ограничения расчета: доступные типы конструкций: трехмерные (стержень, оболочка, твердое тело и все специальные конечные элементы), плоская рама.
- Другие ограничения:
- При корректировке конструкции ограничения не установлены.
Итеративный многоуровневый метод Гаусса-Холецкого
Этот метод работает значительно медленнее, чем итеративный многоуровневый метод ICCF. Однако он требует значительно меньше оперативной памяти.
Метод сглаживания 2 обычно требует меньшее количество итераций по сравнению с итерационным многоуровневым методом ICCF.
Проверка каждого элемента матрицы осуществляется с помощью процедуры регуляризации Vinget 1,2.
- Использование памяти: минимальное
- Использование диска: минимальное
- Оценка скорости: средняя (для хорошо обусловленных задач)
- Количество уравнений: 15 000-1 000 000 и более.
- Поддерживаемые расчеты: линейный статический расчет, модальный расчет и расчет продольного изгиба.
- Возможные ограничения расчета: доступные типы конструкций: трехмерные (стержень, оболочка, твердое тело и все специальные конечные элементы), плоская рама.
- Другие ограничения:
- При корректировке конструкции ограничения не установлены.
Итеративный метод расчета
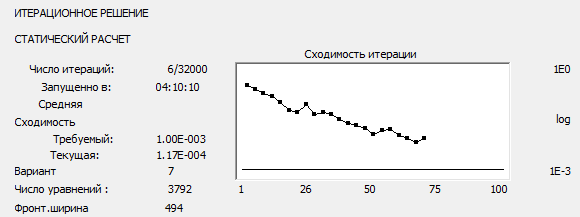
В диалоговом окне "Расчеты" для итерационного метода показан процесс сходимости при условии достижения указанного пользователем уровня точности, либо если процесс является расходящимся.
- номер текущей итерации/максимальное число итераций;
- требуемая точность;
- точность текущей итерации:
- количество уравнений;
- ширина фронта.