Статические силы, приложенные к конструкции, влияют на частоту колебаний конструкции. Используемый обычно модальный расчет (определяющий колебания конструкции) не распознает влияния статических сил. Для аппроксимации реальных условий, в которых работает конструкция, программа Robot может выполнять вычисления, используя Модальный анализ, распознающий приложенные статические силы.
Расчеты колебаний конструкции с распознаванием действия статических сил выполняются в два этапа: Эти расчеты основаны на взаимосвязи между напряжением и деформацией под влиянием заданной статической нагрузки.
Первый этап: Линейный.
где
Xst - Неизвестный вектор статическое состояние
b – вектор заданной статической нагрузки (вектор статической нагрузки),
K — матрица жесткости
L (xst, b) - нелинейных оператор.
Вектор статической нагрузки b может быть простым нагружением или комбинацией заданных нагружений.
Второй этап: Модальный анализ (нелинейный).
, ( 2a )
где
Ks - матрица жесткости, создаваемая на основе напряжений в статическом состоянии.
M – матрица масс.
ωи2 - собственное значение (ωI = пульсация).
Φ - собственный вектор.
Для решения нелинейной статической задачи (модальной) используются те же методы, что и для нелинейного статического расчета. Для линейного статического задачи, имеет место следующее соотношение: 
, где G - геометрическая матрица жесткости.
Положительные значения ωI (ωI > 0) описывают устойчивые состояния равновесия, в то время как отрицательные значения (ωI < 0) соответствуют нестабильному состоянию равновесия. В свою очередь, нулевое значение (ωI = 0) указывает на отсутствие устойчивости (изгиб).
Если матрица K + Ks (xst) перестает быть положительно определенной, это означает, что статическая нагрузка приближается к критическому значению (продольному изгибу). Во время анализа нелинейной статической задачи (модальной) сходимость не достигается. Если выбирается линейный метод (этап Статического анализа) и матрица не определяется как положительная (в этом случае появляется предупреждение), то рекомендуется прекратить процесс вычисления, так как дальнейшие вычисления не имеют смысла.
Пример:
Рассмотрим пример конструкции, показанной на рисунке ниже. N относится к статической нагрузке.
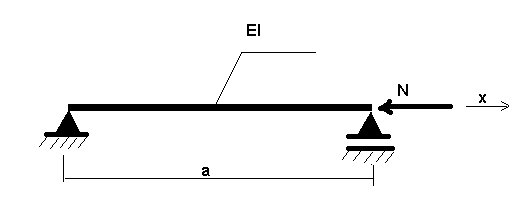
Ниже приведена формула, описывающая поведение приведенной выше конструкции.
, ( 3 )
где
w –перемещения в результате изгиба,
ρ - Плотность материала,
F – площадь поперечного сечения.
Для решения этой задачи перемещение представляется в виде:
( 4 )
Введя выражение ( 4 ) в формулу ( 3 ), получим:
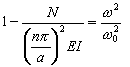, ( 5 )
где
- критическая нагрузка,
ω02 - собственное значение при N=0 (результат правильного модального расчета).
После преобразования последней формулы получаем:
, ( 6 )
где ω2 - собственное значение, полученное для конструкции, с подверженной статической нагрузкой N.
Результат произведенных расчетов представлен графически на рисунке ниже.
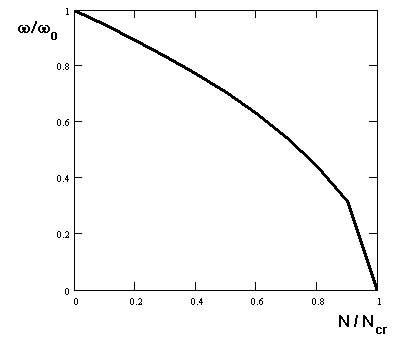
В заключение следует отметить, что для реальной конструкции корреляция w = w(b) выполняется несколько сложнее, чем это представлено в формуле ( 6 ).