Модальный расчет определяет собственные значения и производные значения (собственные пульсации, собственные частоты или собственные периоды), точность, собственные вектора, коэффициенты согласования и согласованные массы для задач собственных колебаний конструкции.
Доступны три режима динамического расчета конструкции (модальный, сейсмический и сейсмический (псевдо режим)).
Собственные значения и собственные формы определяются уравнением:
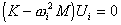(1)
где:
K - матрица жесткостей конструкции,
M - матрица масс конструкции,
ω i - свободные колебания (круговая частота) формы "i",
Ui - вектор собственной формы "i".
Число рассматриваемых собственных форм может быть задано следующим образом:
- верхним пределом пульсации, частоты или периода;
- нижним пределом суммы согласованных масс (выраженного в процентах), либо как действительное число требуемых форм.
Если число форм не задано, то используется значение по умолчанию, заданное в Опциях.
Управляющими параметрами для алгоритма собственной задачи являются следующие параметры:
- точность вычислений (количество ошибок);
- максимальное число повторений.
В программе доступны следующие типы матрицы масс:
- согласованный тип (всегда согласованна с учетом степеней свободы вращения);
- сосредоточенный с вращением (диагональная матрица с учетом степеней свободы вращения),
- сосредоточенная без вращений (диагональная матрица масс без учета вращательных степеней свободы).
Сосредоточенная матрица масс создается в соответствии с правилом:
Mlum(i, j) = 0,0; для i ≠ J
Mlum (i, j) = Stot/Sdiag * М(i, j); для i=j (2)
где:
Stot - сумма всех элементов согласованной матрицы масс M,
Sdiag - сумма диагональных элементов согласованной матрицы масс M.
Таким образом, масса элемента является постоянной, и матрица масс элементов является положительно определенной.
Собственные вектора, показанные в результирующих модулях, нормализованы таким образом, что максимальный член каждого вектора равен 1,0.
Внешние собственные вектора, используемые во время вычислений, нормализованы таким образом, что:
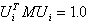(3)
Значение точности, которое выводится в диалоговом окне собственных значений, рассматривается как достигнутая точность сходимости. Эта величина означает, насколько точно собственное значение λiсобственный вектор Ui, достигнутые в процессе итерации i-ой формы, соответствуют уравнению собственной задачи:
K * Ui = λi * M * Ui(4)
Коэффициенты согласования определяются как:
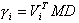
где:
D - единичный вектор, определенный как:
D(j) = 1,0 если j равно i-ой степени свободы
D(j) = 0,0 если j № i,
Vi - собственный вектор формы i , нормализованный следующим образом
:
Согласованные – это динамические массы, согласованные в движении конструкции для каждой формы и каждой степени свободы. Они рассматриваются как текущие массы для текущей формы и как связанные массы, которые являются суммой текущих масс от первой формы до соответствующей текущей формы. Значения представлены как процент от общих динамических масс.
Текущие согласованные массы определяются следующим образом:
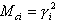
В настоящее время алгоритм Ланцоша, который представляет собой мощное средство решения задач собственных значений высокого порядка(1), является основным методом решения собственных задач. Он позволяет находить требуемые n собственных значений и собственных векторов с любой точностью.
В большинстве случаев метод Ланцоша рекомендован как наиболее эффективный. Тем не менее, он имеет следующие ограничения:
- трех диагональная матрица T не должна быть согласованного типа;
- матрица масс M должна быть Сосредоточенной с вращением или Согласованной. Если выбрана Сосредоточенная без вращения то матрица масс автоматически меняется на Сосредоточенную с вращением.
Если выбран метод Ланцоша, метод вычислений в программе изменяется на метод итераций в подпространствах. Тем не менее, если требуется использовать в расчетах метод Ланцоша, то разделенные конструкции должны быть связаны таким образом, чтобы модель конструкции была неизменна (например, должен быть добавлен стержень на опорах).
В методе Ланцоша применяется следующее приведение трех диагональной матрицы T:
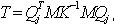
где
Qj = {q1, q2,..., qj}- прямоугольная матрица Neq x j, Neq - количество уравнений, j- количество шагов по Ланцошу , qj - j-тый вектор Ланцоша .
Формула
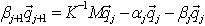
используется для генерации следующего вектора Ланцоша qj+1 и устанавливает текущую строку матрицы T.
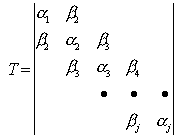
Таким образом, приведенная собственная задача выглядит так:
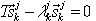, k=1,2,..., j
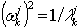, где ωk j является j-той аппроксимацией ω, k=1,2,..., n, и n является требуемое количество собственных значений и векторов. Программа продолжает вычисления (увеличение j – числа шагов Ланцоша) до тех пор, пока не будет достигнута требуемая точность для всех собственных значений n.
Процедура ортогонализации поддерживает требуемый уровень ортогональности между векторами Ланцоша, который обеспечивает сохранность и числовую стабильность вычислений.
Собственные вектора получаются по следующей формуле:
U = Qs.
Основной редуктивный метод
Основной редуктивный метод позволяет получать приближенные значения нескольких первых собственных значений при условии, что некоторые данные о них уже собраны. Этот метод требует назначения степеней свободы (MDOF) для получения приведенной системы. Благодаря этому методу из приведенной модели могут быть исключены несущественные степени свободы, что уменьшает размер решаемой задачи. Метод особенно полезен для пользователей, имеющих опыт динамического расчета конструкции, а также в случаях, когда поведение динамической конструкции заранее известно.
К данному методу применимы следующие правила:
- Должна быть задана главная степень свободы MDOF, (главные узлы и направления). Подразумевается, что в качестве главной степени свободы могут быть приняты только перемещения (не вращения).
- Любой тип матрицы массы может использоваться в алгоритме. Однако, Сосредоточенный без вращения тип матрицы обеспечивает кратчайший период расчета.
- Проверка Штурма указывает число пропущенных частот. Эти значения и собственные векторы не будут найдены. Единственный способ достичь сходимости – это увеличить число MDOF, для того чтобы решить задачу и сравнить собственные векторы.
Метод включает в себя изменение в большинства собственных задач для форм МКЭ.
K U - ω2 M U = 0 к собственной задаче меньшего размера для приведенной модели:
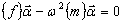
где {f} – матрица воздействия, {m} – обобщенная матрица для упрощенной модели.
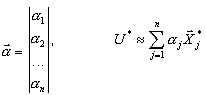
Основой для таких преобразований являются решения, полученные для соответствующих состояний блоков:
узловые силы прикладываются последовательно к каждому узлу главного типа в выбранном направлении главного типа. Крупномасштабная статическая задача решается для n правых частей:
K Xi * = Ti, i = 1, 2,..., n
где Ti - вектор нагрузки, соответствующие i-той единицы силы. Когда узлы и направления главного типа определены, все остальные операции производятся автоматически. Затем, приведенная собственная задача решается методом Якоби. В результате будут получены приблизительные значения частот wi и собственных векторов Ui *, i=1,2,..., N .
См. также:
Модальный расчет - Точность вычислений при модальном расчете конструкции